Абитуриенту

В.М.Буханов, А.В.Грачёв, В.А.Погожев,
В.С.Степанова, Н.И.Чистякова, А.А.Якута
yakuta@genphys.phys.msu.su

Физфак МГУ-2003

Вступительные испытания по физике

Окончание. См. № 2/05

3 Точечный источник S, дающий свет длиной волны , помещён в фокус собирающей линзы Л. За линзой находится призма П из стекла с показателем преломления n и преломляющим углом За призмой расположен экран Э, плоскость которого параллельна передней грани призмы и перпендикулярна главной оптической оси линзы (см. рис. 3). С какой скоростью нужно начать двигать экран параллельно этой оси, чтобы количество наблюдаемых на нём интерференционных полос начало увеличиваться на N полос в расчёте на единицу времени, если первоначально экран находился достаточно близко от призмы?

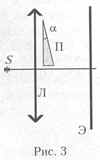
Решение

Будем считать, что диаметр линзы существенно меньше её фокусного расстояния, т.е. будем решать задачу в параксиальном приближении. Поэтому можно считать, что выходящие после преломления в собирающей линзе лучи от точечного источника, помещённого в главном фокусе линзы, параллельны главной оптической оси линзы. Учитывая, что, по условию задачи, главная оптическая ось линзы перпендикулярна передней грани призмы, а радиус линзы, судя по рис. 3, больше размеров этой грани, следует считать, что вся призма полностью залита светом и падающий на неё пучок проходит через переднюю грань, не изменяя направления своего распространения.

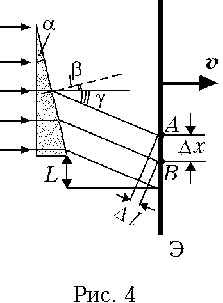
Согласно закону преломления и с учётом принятых на рис. 4 обозначений можно утверждать, что выходящие из призмы лучи образуют с падающими на призму лучами угол причём По условию задачи, Вспоминая, что синус малого угла примерно равен самому углу, измеренному в радианной мере, получим

Интерференционная картина может наблюдаться только в области перекрытия падающих на экран Э лучей, т.е. согласно обозначениям на рис. 4 на отрезке длиной L.

Поскольку экран перпендикулярен главной оптической оси линзы, то его поверхность параллельна волновому фронту света, прошедшего через линзу. Следовательно, разность фаз колебаний, создаваемых лучами, попадающими на экран, минуя призму, во всех точках экрана равна нулю. Поэтому, если в точке А на экране наблюдается интерференционный максимум, то в точке В будет наблюдаться ближайший к нему интерференционный максимум, если разность хода l лучей, прошедших через призму и попадающих в указанные точки, равна . Следовательно, ширину x интерференционной полосы можно найти из соотношения

При удалении экрана от призмы со скоростью   размер L области интерференции за время t увеличивается на L = t tg . Согласно условию задачи число интерференционных полос на экране должно увеличиваться на N штук в расчёте на единицу времени. Следовательно, должно выполняться соотношение

Поскольку, по условию задачи, то и а потому искомую скорость движения экрана можно считать равной

4   Человеку, идущему по горизонтальному участку дороги в пасмурный безветренный день, небольшая лужа, видневшаяся вдалеке на дороге, показалась синего цвета. На каком расстоянии s от этой лужи она будет казаться человеку зелёной? Считать, что глаза человека находятся всё время на высоте h = 1,85 м от дороги. Показатель преломления очень тонкой плёнки бесцветного масла на поверхности лужи равен n = 1,5, а воды –
n_в = 1,33. Длину волны света синего цвета считать равнойс = 0,43 мкм, а зелёного – з = 0,53 мкм.

Решение

По условию задачи, рассматриваемые события происходят в пасмурный безветренный день. Поэтому можно считать, что границы воздух–масло и масло–вода совпадают с горизонтальными плоскостями, а лужа освещается рассеянным белым светом. Изменение же цвета лужи обусловлено явлением интерференции света, отражающегося от указанных границ. Учитывая малый размер зрачка глаз человека по сравнению даже с минимально возможным расстоянием от глаз до поверхности лужи, попадающие в глаз человека световые лучи следует считать параллельными. Согласно рис. 5, а эти лучи образуют с горизонтом угол , определяемый соотношением tg  = h/s.

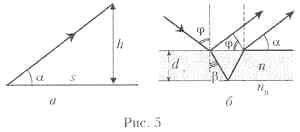
На рис. 5, б показаны два из регистрируемых человеком лучей. Первый луч возникает при отражении от верхней, а второй – от нижней поверхностей масляной плёнки. Поскольку показатель n преломления масла больше не только показателя преломления воздуха (n_вз 1), но и показателя преломления воды, то на верхней границе масла разность фаз падающего и отраженного света равна , а на нижней границе масла она равна нулю. Другими словами, при отражении от оптически более плотной среды происходит «потеря половины длины волны» падающего света. Поэтому величину разности хода между лучами 1 и 2, возникающими при отражении луча, падающего на плёнку масла под углом   к вертикали, в соответствии с обозначениями на рис. 5, б можно вычислить по формуле

где d – толщина масляной плёнки, а угол , согласно закону преломления, определяется из соотношения С учётом этого соотношения формулу для вычисления разности хода можно представить в виде:

Вспоминая условия образования максимумов в интерференционной картине и учитывая, что плёнка масла, по условию задачи, является очень тонкой, можно утверждать, что цвет лужи, когда человек находится от неё на расстоянии s, должен соответствовать такой длине волны света (s), что s = (s). Следовательно, когда человек первоначально заметил лужу, т.е. при (или ) должно было выполняться соотношение

а в тот момент, когда кажущийся человеку цвет лужи стал зелёным, попадающие в глаз человека лучи образуют с горизонтом такой угол _з, что

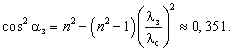
Следовательно, человек увидел лужу зелёной, когда он подошел к ней на расстояние