Абитуриенту

В.М.БУХАНОВ, А.В.ГРАЧЁВ, В.А.ПОГОЖЕВ,
Н.И.ЧИСТЯКОВА, А.А.ЯКУТА
yakuta@genphys.phys.msu.su

Физфак МГУ-2003
Вступительные испытания по физике

III. Электродинамика (окончание)

8 В достаточно большой области в вакууме, разделённой на две части плоской границей, созданы однородные магнитные поля, линии индукции которых направлены одинаково и параллельно границе раздела. Величина индукции магнитного поля в первой части равна В₁, а во второй равна В₂, причём В₁ > B₂. Границу раздела по нормали к ней пересекает электрон, движущийся из первой части области во вторую. Пренебрегая излучением, найдите отношение величины перемещения электрона к пройденному им пути за достаточно большой промежуток времени.

Решение

На электрон, движущийся в магнитном поле, действует так называемая магнитная составляющая силы Лоренца: Эта сила направлена перпендикулярно как вектору скорости электрона, так и вектору В индукции магнитного поля. Поэтому указанная сила не будет совершать работы над электроном, но будет сообщать ему центростремительное ускорение. Поскольку, по условию задачи, потерями энергии электрона при его движении следует пренебречь, то величину скорости электрона следует считать постоянной. Следовательно, можно утверждать, что электрон в каждой из областей должен двигаться по дугам окружностей, радиусы которых определяются выражением

где m – масса, а е – заряд электрона.

По условию задачи, электрон пересекает границу раздела по нормали к ней. Поэтому траектория электрона, имеющего, как известно, отрицательный заряд, состоит из чередующихся полуокружностей, как показано на рис. 6, т.к., по условию, В₁ > B₂. Из этого рисунка видно, что электрон периодически пересекает границу раздела, изображённую на рис. 6 пунктирной линией. При этом он смещается вдоль границы на расстояние за промежуток времени

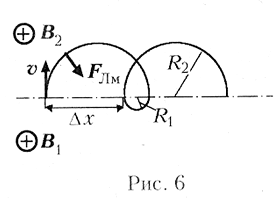
Поскольку удаление электрона от границы раздела не превышает R₂, то величина перемещения электрона по мере увеличения времени    его движения будет стремиться к величине При этом пройденный путь будет равен Следовательно, отношение величины перемещения электрона к пройденному им пути за достаточно большой промежуток времени следует считать равным

9 Напряжение U между клеммами В и С в схеме, показанной на рис. 7, изменяется с периодом Т по закону, изображённому на графике. Найдите эффективное значение силы тока через амперметр А. Сопротивления всех резисторов одинаковы и равны R. Внутренним сопротивлением амперметра пренебречь. Диоды считать идеальными.

Решение

Если, как это обычно и делается при решении подобных задач, пренебречь индуктивностью элементов схемы и емкостями между ними, то изменение силы тока, текущего через амперметр, согласно заданному в условии задачи закону изменения напряжения, должно происходить скачкообразно в моменты, соответствующие моментам изменения полярности напряжения между клеммами В и С, т.к. в остальные моменты времени напряжение между указанными клеммами остаётся постоянным. Напомним, что идеальным называют такой диод, сопротивление которого равно нулю, если потенциал анода (основания треугольника, с помощью которого изображается диод) выше потенциала катода, а при обратной полярности приложенного к диоду напряжения равна нулю его проводимость. Следовательно, если потенциал клеммы В ниже потенциала клеммы С, то диоды D₁ и D₂ будут находиться в проводящем состоянии, а потому сопротивление между указанными клеммами с учётом сделанных предположений и условия задачи будет равно сопротивлению параллельно включённых резисторов R₂ и R₃. Поэтому, согласно закону Ома для участка цепи, не содержащего ЭДС, во время отрицательной полуволны напряжения через амперметр должен протекать ток

Во время другой части периода длительностью
T – потенциал клеммы В превышает потенциал клеммы С. Поэтому в это время диод D₁ должен быть заперт, а диод D₂ открыт, т.к. потенциал его анода и в этом случае будет превышать потенциал катода. Следовательно, текущий через амперметр ток во время указанной части периода должен быть равен

Поскольку эффективным, или действующим, значением силы периодически изменяющегося тока называют величину такого постоянного тока, при протекании которого по некоторому резистору за время, равное периоду переменного тока, на резисторе выделяется такое же количество теплоты, как и при протекании заданного переменного тока за то же время, то искомое эффективное значение силы тока при выполнении сделанных предположений равно:

10  Из изолированной тонкой проволоки изготовлена замкнутая плоская петля, состоящая из двух окружностей (рис. 8). Радиус большой окружности равен R₁, малой – R₂. Петля находится в однородном магнитном поле, перпендикулярном её плоскости. Индукция поля возрастает с постоянной скоростью. Во сколько раз изменится разность потенциалов между точками, расположенными одна над другой в месте скрещивания проводов, если меньшую окружность повернуть вокруг оси ОО на 180°?

Решение

При решении задачи будем пренебрегать магнитным потоком, пронизывающим материал проволоки, поскольку, по условию задачи, проволока является тонкой. В силу этой же причины площадь, ограниченную каждой из окружностей, образующих петлю, следует считать равной , где R_i – радиус i-й окружности. Тогда, учитывая, что скорость   нарастания индукции внешнего магнитного поля, по условию задачи, постоянна, и считая, как это обычно делается при решении подобных задач, источник магнитного поля и петлю покоящимися относительно некоторой инерциальной системы отсчёта, на основании правила потока Фарадея–Максвелла (закона электромагнитной индукции) можно утверждать, что величины ЭДС в первой и второй частях петли равны Сказанное верно в предположении, что ток в петле достиг установившегося значения, или в предположении, что скорость изменения индукции магнитного поля, порождаемого током в петле, значительно меньше . Заметим, что последнее эквивалентно предположению о возможности пренебречь индуктивностью петли.

Если за положительное принять направление тока, который существовал бы в петле в отсутствие ЭДС во второй её части, то действующую в первой части петли ЭДС следует также считать положительной. По условию задачи, сторонние электрические силы, действующие в кольцах петли до поворота меньшей окружности, направлены в противоположные стороны, т.к. направления обхода колец взаимно противоположны (см. рис. 8). Поэтому, согласно закону Ома для замкнутой цепи, установившийся ток в петле до поворота малой окружности должен быть равен

где r₁ и r₂ – сопротивления большой и малой окружностей соответственно. Отсюда на основании закона Ома для участка цепи, содержащего ЭДС, следует, что в рассматриваемом случае разность потенциалов между заданными точками равна .

После заданного поворота на 180° малой окружности действующая в ней ЭДС изменяет направление на противоположное. Поэтому при выполнении сделанных ранее предположений установившийся ток в петле станет равным

а интересующую разность потенциалов можно будет найти по формуле

Поскольку сопротивления первой и второй окружностей прямо пропорциональны их радиусам, то, считая, что при изменении силы тока в петле удельное сопротивление проволоки остаётся неизменным, из приведённых выше соотношений получаем искомое отношение разностей потенциалов между заданными точками петли:

IV. Оптика

1 Цилиндрическое ведро диаметром d и высотой h = 1,5d, наполовину наполненное прозрачной жидкостью, начинают двигать поступательно в горизонтальном направлении с медленно увеличивающимся ускорением а. В центре дна ведра вмонтирован лазер Л, испускающий узкий параллельный пучок света вертикально вверх вдоль оси ведра. Стенки ведра полностью поглощают падающий на них свет. Найдите показатель преломления жидкости, если свет перестаёт выходить из ведра, когда величина ускорения а становится равной величине g ускорения свободного падения.

Решение

При движении ведра с медленно увеличивающимся ускорением в горизонтальном с точки зрения неподвижного наблюдателя направлении жидкость будет монотонно перемещаться внутри ведра. Когда же ускорение перестанет изменяться, прекратится и движение жидкости относительно ведра, а её поверхность не будет горизонтальной.

Чтобы найти форму поверхности жидкости при движении ведра с постоянным ускорением, воспользуемся инерциальной декартовой системой координат, ось Х которой совпадает с направлением ускорения а, ось Y направлена горизонтально, а ось Z направлена вертикально вниз. Мысленно выделим внутри жидкости объём массой m, имеющий форму прямоугольного параллелепипеда с рёбрами, параллельными осям выбранной системы координат. На грани этого объёма со стороны остальной части жидкости могут действовать силы, направленные только перпендикулярно этим граням внутрь выделенного объёма, т.к. жидкость обладает свойством текучести. Поскольку ускорение всех точек этого объёма одинаково и направлено вдоль оси Х, разность сил давления на боковые грани, перпендикулярные этой оси, должна быть равна ma; на боковые грани, перпендикулярные оси Y, равна нулю; на нижнюю и верхнюю грани – силе тяжести mg. Следовательно, давление внутри жидкости не зависит от координаты y. Если считать, что высота выделенного объёма достаточно мала, то давление р(х) во всех точках грани, перпендикулярной оси Х, можно считать постоянным, а разность сил давления на заднюю и переднюю грани в соответствии со вторым законом Ньютона можно представить в виде:

Будем считать плотность жидкости постоянной и равной , т.к. иное специально не оговорено в условии задачи. Тогда из предыдущего соотношения получим

Записав уравнение движения выделенного объёема жидкости в проекциях на ось Z при условии, что длина ребра достаточно мала, можно доказать, что давление в жидкости в рассматриваемом случае по мере увеличения координаты z на величину увеличивается по закону

Следовательно, давление внутри слоя жидкости, все точки которого имеют одинаковую координату z, должно возрастать по линейному закону по мере удаления от передней стенки ведра к задней, а все точки поверхности жидкости, имеющие одинаковую координату х, должны лежать на прямых, параллельных оси Y. Образованная этими прямыми поверхность жидкости в ведре, движущемся с постоянным ускорением а, имеет вид части плоскости, образующей с плоскостью z = const такой угол , что

.

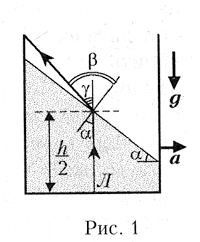
На рис. 1 показано сечение ведра вертикальной плоскостью, проходящей через ось ведра параллельно его ускорению а. Поскольку ведро было наполнено жидкостью лишь наполовину и высота ведра h превышает его диаметр d в полтора раза, то при a = g жидкость не будет выливаться из ведра, а её поверхность будет пересекать ось ведра на расстоянии 0,5 h от дна. На этом же рисунке сплошной линией со стрелкой показан ход луча, испускаемого лазером Л. При построении предполагалось, что показатель преломления n не зависит от давления в жидкости, и выполняются законы прямолинейного распространения и преломления света, т.к. ускорение ведра достаточно мало.

Поскольку стенки ведра полностью поглощают падающий на них свет, то свет не будет выходить из ведра, если преломленный луч попадёт на стенку. Из рисунка видно, что это будет иметь место, если угол между преломленным лучом и вертикалью, равный разности углов преломления и падения , будет удовлетворять соотношению По определению, Следовательно,

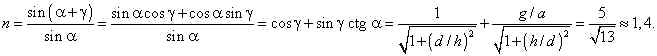
2    С помощью тонкой собирающей линзы получено действительное изображение квадрата, одна из сторон которого совпадает с главной оптической осью линзы. Длина стороны квадрата равна a. При этом площадь изображения оказалась в n раз больше площади квадрата, а отношение длин изображений сторон квадрата, перпендикулярных оптической оси, равным k (k > 1). Найдите фокусное расстояние F линзы.

Решение

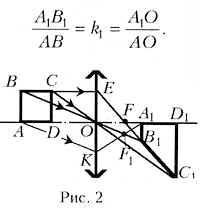
Будем считать, как это обычно и делают при решении подобных задач, что изображение квадрата является стигматичным, т.е. каждой точке квадрата соответствует лишь одна точка на его изображении. Как известно, это условие будет выполнено, если световые пучки, формирующие изображение той или иной точки квадрата, являются достаточно узкими, т.е. справедливо так называемое параксиальное приближение. В этом случае лучи, падающие на собирающую линзу параллельно её главной оптической оси, после преломления будут проходить через её главный фокус F за линзой, а лучи, идущие вдоль побочных оптических осей, т.е. через оптический центр линзы (точка О), будут проходить через линзу без преломления. Все точки квадрата должны находиться от линзы на расстояниях, превышающих её фокусное расстояние. В соответствии со сказанным на рис. 2 выполнено построение изображения квадрата ABCD. Для построения изображения А₁ точки А была найдена точка пересечения двух лучей: луча, идущего вдоль главной оптической оси OF, и луча АК, идущего параллельно побочной оптической оси BB₁. При этом было учтено, что в параксиальном приближении после преломления в линзе все лучи, параллельные оптической оси BB₁, пересекаются в побочном фокусе F₁ – в точке пересечения этой оси с фокальной плоскостью FF₁. Таким образом, изображение заданного квадрата имеет вид трапеции, одна из боковых сторон которой перпендикулярна основаниям.

Из подобия треугольников ОАВ и ОА₁В₁ (или из формулы для поперечного увеличения, даваемого тонкой линзой) следует, что

Аналогично находим коэффициент увеличения стороны квадрата CD:

Согласно формуле тонкой линзы, справедливой при выполнении указанных выше предположений, фокусное расстояние F линзы должно удовлетворять равенствам

Из условия задачи и приведённых соотношений следует, что

а т.к., по условию задачи, k₂/k₁ = k, то основания трапеций равны соответственно:

 ;

Поскольку треугольники OEF, FA₁B₁ и FD₁C₁ подобны, то

а потому фокусное расстояние линзы равно

Продолжение в № 4