Окончание. См. № 4/08

В.В.АЛЬМИНДЕРОВ, А.В.КРАВЦОВ, В.Г.КРЫШТОП,
МИК «Глюон»

gluon@yandex.ru

XVI международная олимпиада

«Интеллектуальный марафон-2007»

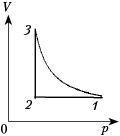
7. Два моля идеального одноатомного газа сначала изохорно охладили, а затем изобарно нагрели до первоначальной температуры 400 К, увеличив объём газа в три раза. Какое количество теплоты отдал газ на участке 1–2?

Ответ. Газ отдаёт тепло на изохорном участке 1–2, следовательно, Q₁₂ = c_V · · T₁₂, где T₁₂ = Т₂ – Т₁. По условию задачи, Т₁ = Т₃, участок 2–3 – изобарный, и для него справедливо откуда получаем Для одноатомного идеального газа поэтому, подставляя полученные результаты в формулу для отданного количества теплоты, получим |Q₁₂| = RТ₁ =
= 6,65 кДж.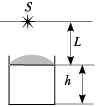

8. В сосуде на поверхности прозрачной жидкости плавает лёгкая тонкая плосковыпуклая линза выпуклой стороной вверх. Фокусное расстояние линзы в воздухе F. Показатель преломления жидкости n. Высота уровня жидкости в сосуде h. На каком расстоянии L над линзой на её главной оптической оси нужно расположить точечный источник света S, чтобы его изображение находилось на дне сосуда?

Ответ. Наличие среды с показателем преломления n со стороны плоской поверхности линзы увеличивает расстояние от линзы до изображения в n раз (в параксиальном приближении). Тогда

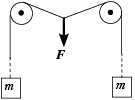
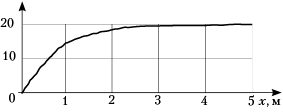
9. Через два неподвижных блока, находящихся на одной высоте, перекинута длинная лёгкая нить, к концам которой прикреплены два груза одинаковой массы. Нить начинают медленно оттягивать вниз за точку, находящуюся посередине между блоками. График зависимости силы F, прикладываемой к нити, от смещения x этой точки также приведён на рисунке.

Найдите приблизительно массу m каждого из грузов и расстояние между блоками.

Ответ. Из приведённого графика видим, что при больших смещениях х сила F стремится к постоянной величине 20 Н. Это говорит о том, что нити становятся практически параллельными, а т.к. смещение под действием силы F происходит квазистатически, то F = 2mg. Откуда mg = 10 Н, m 1 кг.

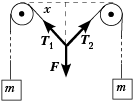
Для оценки расстояния между блоками оценим силу F, когда нити образуют между собой угол, например, 90°. В этом случае или
Этой силе соответствует расстояние х 1 м. Тогда расстояние между блоками приблизительно равно 2 м.

10. Нижние концы лестницы-стремянки массой m = 10 кг соединены верёвкой. Каждая сторона лестницы составляет с полом угол  = 45°. Считая пол абсолютно гладким, найдите силу натяжения верёвки.

Ответ. Особенность этой задачи состоит в том, что силу натяжения нельзя найти из условия равновесия (ни из уравнения для сил, ни из уравнения моментов) лестницы как целого, т.к. она является внутренней силой. Для нахождения этой силы запишем уравнение моментов для правой части лестницы относительно оси соединения сторон лестницы-стремянки (верхняя точка О на рисунке):

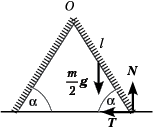
Реакцию опоры N найдём из проекции на вертикальную ось уравнения для сил: 2N – mg = 0.

Тогда сила натяжения

Раздел «Задачи по физике для письменного тура»

1. Искусственный спутник Земли находится на круговой орбите высотой h = 200 км. Включается двигатель, и скорость спутника возрастает на = 5 км/с. В результате он улетает в межпланетное пространство. Найдите скорость спутника вдали от Земли. Радиус Земли 6370 км, ускорение свободного падения на поверхности Земли 9,8 м/с².

Ответ.   где M_З – масса Земли.

Для круговой орбиты   откуда

По закону сохранения механической энергии,

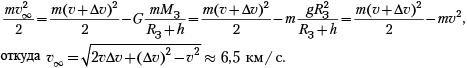
2. Известно, что компрессор домашнего холодильника периодически включается и выключается. Оцените соотношение времён работы и паузы компрессора, если известно, что его мощность около 100 Вт, через стенки холодильника за час проходит количество теплоты, равное 1 МДж, температура в помещении, где стоит холодильник, t₁ = 20 °С, температура внутри холодильника t₂ = 3 °С.

Ответ. Оценим минимальную среднюю мощность компрессора, необходимую для поддержания заданной температуры внутри холодильника. Допустим, что в холодильнике осуществляется обратный цикл Карно. Тогда при температуре T₂ отбирается количество теплоты Q₂ (именно эта энергия «просачивается» в холодильник сквозь стенки), окружающей среде отдаётся при температуре T₁ количество теплоты Q₁, при этом совершается работа A = Q₁ – Q₂.

Холодильный коэффициент в обратном цикле Карно

Работа компрессора связана с отбираемым количеством теплоты: Q₂ = _xA. После несложных преобразований получим

Подставив численные значения, получим среднюю мощность за время :

Вт.

Чтобы обеспечить такую среднюю мощность, двигатель мощностью 100 Вт должен работать примерно одну шестую часть времени цикла работа–покой.  Реальный  холодильник   работает  не  по  циклу  Карно   (реальные  процессы  вообще   необратимые), поэтому нужна несколько бльшая средняя мощность, и «рабочая» доля времени также увеличится.

3. Оцените, какую мощность имеет 100-ваттная электрическая лампа накаливания в начальный момент включения её в осветительную сеть напряжением 220 В, если рабочая температура нити накаливания составляет 2700 °С, а температурный коэффициент сопротивления вольфрамовой нити накала 0,004 Ом/°С.

Ответ. Зависимость сопротивления от температуры R = R₀(1 + t), где R₀ – сопротивление при 0 °С. Поскольку перепад температур большой, то можно считать, что R₀ – сопротивление при комнатной температуре. Сопротивление горячей нити определим по известной номинальной мощности: R = U²/N = 484 Ом.

Сопротивление холодной нити

Мгновенная мощность при включении т.е. в 12 раз больше номинальной!

4. В камере кольцевого ускорителя по окружности радиусом R движется тонкий пучок электронов. В начальный момент времени значение силы тока I₀, количество частиц в камере N. Магнитный поток через неизменную орбиту пучка уменьшается со скоростью Каким станет значение силы тока после того, как частицы сделают один оборот? Рассмотрите нерелятивистский случай.

Ответ. Сила тока в пучке связана со скоростью частиц следующим образом: I = enS, где e – модуль заряда электрона, n – концентрация заряженных частиц; – скорость частицы; S – площадь пучка. Концентрация электронов ток пучка  Изменение кинетической энергии электрона через один оборот

Поскольку магнитный поток уменьшается, то в соответствии с правилом Ленца ток пучка должен увеличиваться. Cкорость пучка после прохождения одного витка:

5. В чайнике «Тефаль» мощностью 1 кВт кипит вода. С какой скоростью из его носика вырывается струя пара, если площадь отверстия носика S = 5 см², теплота испарения воды r = 2,26 · 10⁶ Дж/кг, нормальное атмосферное давление p₀ = 10⁵ Па, универсальная газовая постоянная R = 8,31 Дж/(моль · К)?

Ответ. Количество теплоты, необходимое для испарения воды массой m, равно Q = rm. Поскольку вся эта энергия идёт на испарение воды, то мощность может быть определена как

Из уравнения Клапейрона–Менделеева найдём, что отсюда скорость испарения

где – искомая скорость струи пара.

В итоге находим

6. При какой минимальной начальной скорости можно перебросить камень с уровня Земли через полуцилиндрический ангар высотой (радиусом) R?

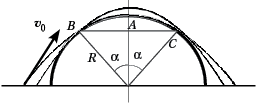
Ответ. Интуитивно представляется, что наименьшей начальной скорости соответствует симметричная траектория, касающаяся ангара в высшей его точке, т. A. Легко показать, что для такой траектории необходимая начальная скорость определяется выражением ₀² = 3gR. Но здесь интуиция нас подводит: в действительности оптимальная траектория касается цилиндра в двух симметрично расположенных точках B и C, положение которых определяется углом = 45°.

Чтобы доказать это, рассмотрим касающуюся цилиндра траекторию с произвольным углом и покажем, что из всего множества таких траекторий наименьшему значению полной механической энергии соответствует траектория с = 45°.

Пусть – величина скорости камня в точке B. Время t полёта камня от B до C запишем двумя способами: как отношение расстояния от B до C по горизонтали к (неизменной) горизонтальной проекции скорости cos, т.е. как t =2Rsin/(cos), и как время подъёма от B до вершины траектории и падения до C с ускорением свободного падения g: t = 2sin/g.

Приравнивая правые части этих выражений, получаем следующее выражение для квадрата необходимой скорости камня в точке B:
² = gR/cos. Будем считать потенциальную энергию камня равной нулю на уровне Земли. Тогда полная энергия камня при движении по рассматриваемой траектории пропорциональна следующему выражению: gR/cos + 2gRcos. Легко видеть, что минимум полной энергии будет при = 45°, когда Таким образом, для траектории с минимальной энергией квадрат скорости в точке B даётся выражением С помощью закона сохранения энергии находим соответствующую этой траектории начальную скорость (скорость на уровне Земли): (что немного меньше значения 3gR, соответствующего траектории, проходящей через точку A).

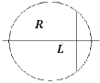7. Металлический шар радиусом R, полный заряд которого равен Q, разрезан на две части. Плоскость разреза проходит на расстоянии L от центра шара (L < R). С какой силой отталкиваются эти части шара?

Ответ. Заряд металлического шара равномерно распределён по его поверхности с поверхностной плотностью На заряд каждого элемента поверхности действует сила со стороны зарядов всей остальной части поверхности. Эта электростатическая сила направлена по нормали к поверхности шара (по радиусу) наружу, что можно рассматривать как некоторое давление p изнутри шара на его поверхность, как если бы шар был изнутри заполнен газом. Легко показать, что это давление равно Сила отталкивания примыкающих одна к другой частей шара равна произведению этого давления на площадь разреза:

Сила отталкивания частей шара будет наибольшей, когда L = 0, т.е. когда шар разрезан по диаметру.