Окончание. См. № 3/08

М.Ю.ДЕМИДОВА, demidovaktv1@yandex.ru,
Г.Г.НИКИФОРОВ, г. Москва

Основные результаты ЕГЭ-2007 по физике

Анализ выполнения заданий с развёрнутым ответом (часть 3 заданий ЕГЭ)

По традиции использовались расчётные задачи высокого уровня сложности (уровня вступительных экзаменов в вузы) по четырём разделам школьного курса физики. К их выполнению приступали в среднем 63% от общего числа тестируемых. В отличие от части 1, которая по силам всем, эти задачи решают в основном учащиеся, получающие на ЕГЭ отметки «4» и «5». Поэтому здесь гораздо меньше заметно влияние трудностей в математике как на выбор задач, так и на их решения. Преимущество отдаётся задачам с типовыми формулировками, с ясной физической ситуацией, хотя и требующими довольно трудоёмкого решения системы уравнений. Предпочтение отдаётся задачам по механике на законы сохранения энергии и импульса (приступает к решению 63%), на применение первого закона термодинамики к изопроцессам (46%), а также на применение законов постоянного тока (45%). Задачи же с новой ситуацией оказываются существенно менее привлекательными. Например, задачи на дифракцию электронов на кристалле рискнули начать делать всего 16% тестируемых.

Наиболее высокие результаты были показаны при решении задач по механике, МКТ и термодинамике, хотя и с нетрадиционной формулировкой. Например:

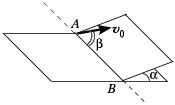
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями  = 30°. Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью ₀ = 2 м/с под углом  = 60° к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Образец решения этой задачи, приведённый в материалах для экспертов, был выполнен, исходя из уравнений кинематики, но многие выпускники использовали для решения задачи закон сохранения энергии. К сожалению, при выполнении этих задач очень распространёнными были ошибки в геометрических преобразованиях и записи проекций векторов на выбранные оси, что существенно повлияло на общие результаты.

Среди заданий по электростатике и постоянному току затруднения вызвала задача на колебания заряженного шарика над заряженной плоскостью. При этом к её выполнению приступали в среднем 32% тестируемых, но 17% получили 0 баллов (т.е. не смогли понять, как заряженная плоскость влияет на колебания маятника), 9% смогли записать уравнение для периода колебаний маятника и силу, действующую на заряд в электростатическом поле, получив за это 1 балл, и лишь 6% смогли с разной степенью успешности довести эти преобразования до ответа и набрали 2–3 балла.

Как и в предыдущие годы, наименее привлекательными для выпускников оказались задачи по оптике. Причём две относились к известным сюжетам (интерференция и изображение в линзе), а одна была сформулирована таким образом, что требовалось сначала самостоятельно выделить явление полного внутреннего отражения. Все имели примерно одинаковый объём и сложность математических преобразований. Невысокие результаты выполнения были вполне запланированы для задачи на полное внутреннее отражение, но для задачи по геометрической оптике (см. пример) оказались гораздо ниже: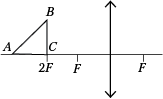

Равнобедренный прямоугольный треугольник ABC площадью 50 см² расположен перед тонкой собирающей линзой так, что его катет AC лежит на главной оптической оси линзы. Фокусное расстояние линзы 50 см. Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки C равно удвоенному фокусному расстоянию линзы. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Эту серию задач выбрали чуть более половины учащихся, однако 27% не сумели справиться с построением изображения треугольника в линзе и получили 0 баллов. Камнем преткновения оказалось построение изображения вершины А. Можно предположить, что сокращение часов на изучение физики в школе не даёт возможности даже при подготовке к ЕГЭ показать приёмы построения в линзе изображения точек, лежащих на её главной оптической оси, при помощи побочной оптической оси. Как правило, после верного построения изображения треугольника применение формулы линзы и нахождение площади треугольника-изображения не вызывало существенных трудностей. Но довести решение до «идеала» удалось лишь 8% тестируемых.

Второй год подряд в варианты включаются задачи на интерференцию в тонком клине. Так, в 2006 г. с задачей на интерференцию света в мыльной плёнке, имеющей форму клина, справились лишь 3% тестируемых. В этом году с аналогичной задачей на интерференцию в клине из стеклянных пластинок справились 4%. Надо сказать, что старый сюжет не сильно сказался на популярности задачи: в прошлом году её выбрали около 15%, в этом – около 18%, с теми же результатами. Поскольку для решения задачи необходимо знать лишь условие для наблюдения максимума (минимума) интерференции и соотношения для прямоугольного треугольника, то столь низкий результат вызван не математическими трудностями, а отсутствием опыта решения задач подобного типа.

Следует отметить, что описанные выше задачи (на построение изображения в линзе, колебания заряженного маятника в электростатическом поле и интерференцию света в клине) являются типовыми лишь для профильного изучения физики, поскольку только в этом случае есть достаточное количество учебного времени. Те, кто изучал курс физики на базовом уровне, оказываются в ситуации практически полной новизны: им известны основные законы, но абсолютно новыми являются ситуации, например, построения в линзе изображений предметов, лежащих на оптической оси, или характера интерференции в клине.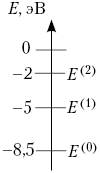

Среди заданий по квантовой физике наиболее сложными оказались задачи на применение законов сохранения энергии при взаимодействии атома с электроном. Например:

Предположим, что схема энергетических уровней атомов некоего вещества имеет вид, показанный на рисунке, и атомы находятся в состоянии с энергией Е⁽¹⁾. Электрон, столкнувшись с одним из таких атомов, в результате приобрёл некоторую дополнительную энергию. Импульс электрона после столкновения с покоящимся атомом оказался равным 1,2 · 10^–24 кг · м/с. Определите кинетическую энергию электрона до столкновения. Возможностью испускания света атомом при столкновении с электроном пренебречь.

К решению этой задачи приступили лишь 26%, из которых 9% смогли записать отдельные элементы решения (изменение кинетической энергии электрона и переход атома на другой энергетический уровень или взаимосвязь импульса с кинетической энергией) и лишь 3% выпускников сумели привести полное правильное решение этой задачи.

В некоторых задачах необходимо было самостоятельно предложить физическую модель, поскольку в тексте в явном виде её описание отсутствовало: колебание груза на пружине, соединённой посредством неподвижного блока с бруском, скользящим по столу; дифракция электронов на кристалле, движение заряженной частицы по окружности под действием кулоновской силы. Объективная сложность новизны ситуации существенно влияет на результаты (выполняемость 4–7%). Например: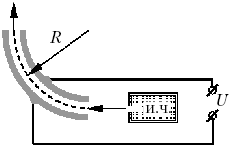

На рисунке показана схема устройства для предварительного отбора заряженных частиц с целью их последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом R  50 см. Предположим, что в промежуток между обкладками конденсатора из источника заряженных частиц (и.ч.) влетают ионы с зарядом –е, как показано на рисунке. Напряжённость электрического поля в конденсаторе по модулю равна 50 кВ/м. Скорость ионов 2 · 10⁵ м/с. Ионы с каким значением массы пролетят сквозь конденсатор, не коснувшись его пластин? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.

Эти задачи решаются практически «в одну формулу», нужно лишь понять, что центростремительное ускорение создаётся кулоновской силой. Как правило, задачи с неявно заданной физической моделью выбирает наименьшее число тестируемых, и для этого типа заданий характерно отличное от типовых задач распределение среднего процента по первичным баллам. Например, для стандартной задачи по механике на применение законов сохранения энергии и импульса распределение таково: 0 баллов – 19%, 1 балл – 16%, 2 балла – 7%, 3 балла – 9%. Понятно, что более половины тестируемых «узнали» условие задачи, а из тех, кто ещё и умел применять законы сохранения к неупругому удару, часть сделали ошибки в записи основных уравнений, а часть не справились с математическими трудностями.

Для задачи же с нестандартной формулировкой условия распределение по баллам выглядит несколько иначе. Например, для вышеприведённой задачи 0 баллов набрали 6%, 1 балл – 3%, 2 балла – 2% и 3 балла – 13%. То есть немногие рискнули начать решать задачу, но те, кто разобрался в описанных процессах, практически «без потерь» сумели довести решение до успешного конца.

Динамика выполнения заданий ЕГЭ в 2002–2007 гг. по отдельным видам деятельности

В КИМах по физике 2007 г. использовалось до 40% заданий прошлых лет. Сравнение результатов выполнения этих групп заданий в ЕГЭ разных лет позволяет выявить динамику усвоения отдельных видов деятельности и элементов содержания.

Около 20% заданий базового уровня в части 1 направлены на проверку узнавания различных законов и формул, а также применения их для анализа несложных процессов на качественном уровне. Наблюдается положительная динамика качества их выполнения, что говорит о том, что основной «перечень формул» курса физики на репродуктивном уровне усваивается достаточно хорошо. Единственным исключением стала в этом году формула для зависимости ёмкости плоского конденсатора от площади пластин и расстояния между обкладками.

Для расчётных заданий на проверку того же перечня законов и формул выполняемость либо та же, либо немного снижена. Например:

• Гидростатическое давление, базовый уровень: 2005 г. – 68%, 2007 г. – 68%.

В сосуд глубиной 20 см налита вода, уровень которой ниже верхнего края сосуда на 2 см. Чему равно давление столба воды на дно?

1) 2 · 10⁵ Па; 2) 2000 Па; 3) 1800 Па; 4) 180 Па.

• Механическая работа, базовый уровень: 2003 г. – 69%, 2007 г. – 63%.

Мальчик везёт своего друга на санках по горизонтальной дороге, прикладывая силу 60 Н. Скорость санок постоянна. Верёвка санок составляет с горизонталью угол 30°. На некотором участке пути механическая работа силы упругости верёвки равна 6000 Дж. Какова длина этого участка пути?

Cкорее всего здесь сказываются проблемы с вычислительными навыками, причём в основном за счёт слабых учащихся.

Некоторый рост выполняемости наблюдается и по самому сложному из проверяемых виду деятельности – решению задач, который занимает больше 30% от всего объёма экзаменационного варианта, причём как по отдельным задачам повышенного уровня с выбором ответа и с кратким ответом, так и по сложным задачам с развёрнутым ответом. Выделить какие-либо общие тенденции сложно, т.к. здесь задачи ежегодно обновляются (лишь 1–2 старые задачи). Например:

• Закон сохранения энергии, повышенный уровень: 2005 г. – 37%, 2007 г. – 41%.

Автомобиль, движущийся с выключенным двигателем, на горизонтальном участке дороги имел скорость 30 м/с. Какой путь он пройдёт вверх по склону горы под углом 30° к горизонту, пока его скорость не уменьшится до 20 м/с? Трением пренебречь.

1) 12,5 м; 2) 25 м; 3) 50 м; 4) 100 м.

• Формула тонкой линзы, повышенный уровень: 2004 г. – 59%, 2007 г. – 65%.

Фокусное расстояние собирающей линзы 60 см. На каком расстоянии от линзы находится мнимое изображение предмета, который расположен на расстоянии 40 см от линзы? Ответ выразите в сантиметрах (см). (Ответ: 120.)

К сожалению, как и в 2006 г., наиболее проблемными оказываются качественные вопросы, проверяющие понимание смысла различных понятий, величин и законов, контролирующие умения объяснять физические явления, выделять условия их протекания или различать проявления этих явлений в окружающей жизни. Для них характерны не только достаточно низкий уровень выполнения и отсутствие положительной динамики, но иногда и снижение результатов.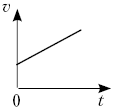

• Равноускоренное движение, повышенный уровень: 2003 г. – 52%, 2005 г. – 54%, 2007 г. – 54%.

На рисунке справа приведён график зависимости скорости тела от времени при прямолинейном движении. Какой из графиков выражает зависимость модуля равнодействующей всех сил, действующих на тело, от времени движения? Систему отсчёта считать инерциальной.

• Постулаты СТО, базовый уровень: 2003 г. – 52%, 2007 г. – 40%.

Какие из приведённых ниже утверждений являются постулатами специальной теории относительности?

А) Принцип относительности – равноправность всех инерциальных систем отсчёта;

Б) инвариантность скорости света в вакууме – неизменность её модуля при переходе из одной инерциальной системы отсчёта в другую.

1) Только А; 2) только Б; 3) и А, и Б; 4) ни А, ни Б.

Наиболее чётко тенденция некоторого снижения качества выполнения заданий проявляется для тех вопросов, на которые в первую очередь сокращают время изучения при общем уменьшении количества учебных часов, отводимых на преподавание физики (например, свойства электромагнитных волн, элементы СТО, ток в различных средах, элементы геометрической оптики и т.п.).

Анализ результатов выполнения работы учащимися, имеющими различные уровни подготовки

Задания базового уровня части 1 позволяют чётко выделить учащихся с неудовлетворительным уровнем подготовки (отметка за экзамен «2»); задания повышенного уровня (А8, А9, А15, А23, А24, В1–В4) – дифференцировать «отличников», «хорошистов» и «троечников», а задания высокого уровня сложности (С1–С6) – выделить «отличников».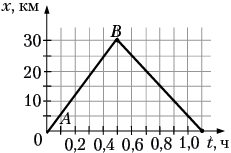

При неудовлетворительном уровне подготовки тестируемые показывают крайне низкий уровень знаний даже основного понятийного аппарата школьного курса физики: выполняемость составляет 29% для заданий с выбором ответа; 5% для заданий с кратким ответом; 0% для заданий с развёрнутым ответом (т.е. отрывочные знания отдельных формул и некоторых явлений). Например, для приведённого графика зависимости координаты тела от времени при его движении из точки А (х = 0) в точку В (х = 30 км) и обратно скорость на участке АВ находит 70% учащихся этой группы, а на участке ВА – только 45%. Стандартное задание рассчитать силу упругости пружины жёсткостью k = ... Н/м, растягивающейся на ... м, выполняют 73%, а удлинение в обратном задании – лишь 48%.

При удовлетворительном уровне подготовки продемонстрировано владение основными законами и формулами школьного курса физики: выполняемость 51% для заданий с выбором ответа; 18% для заданий с кратким ответом; 4% для заданий с развёрнутым ответом. Нет большого разрыва при выполнении однотипных заданий на проверку законов и формул, т.е. влияние математических трудностей при простых расчётах гораздо меньше, чем у предыдущей группы. Например, для серии заданий на силу трения (расчёт коэффициента трения, массы тела, силы трения, силы нормального давления при равномерном движении) выполняемость 55–67%. Практически все усвоенные элементы содержания представляют собой наиболее «прорабатываемые» на уроках законы и формулы. Однако с вопросами качественного характера справляются лишь 50% (правило левой руки, расстановка диапазонов электромагнитных излучений по нарастанию или убыванию длины волны или частоты, закономерности явления электромагнитной индукции и т.п.). Эта группа пытается приступать к выполнению отдельных задач с кратким и развёрнутым ответом, но учащиеся не могут довести решение до конца, как правило, правильно записывая условие задачи и отдельные уравнения для её решения. Приоритетными здесь являются задачи по механике на законы сохранения энергии и импульса, по электродинамике на запись закона Ома для полной цепи и формулы для силы Лоренца.

При хорошем уровне подготовки тестируемые показывают систематические знания школьного курса физики при выполнении заданий базового и повышенного уровней сложности: 74% для заданий с выбором ответа; 48% для заданий с кратким ответом; 22% для заданий с развёрнутым ответом. Они справляются с большинством вопросов качественного характера, проверяющих особенности протекания явлений. (Слишком сложными – выполняемость меньше 50% – оказались лишь две серии заданий базового уровня: поведение диэлектрика в электрическом поле и изменение количества фотоэлектронов при изменении энергии падающего света.) Эта группа довольно успешно выполняет ряд заданий повышенного уровня как с выбором ответа, так и с кратким ответом (20–75%). По сравнению с прошлым годом улучшились результаты выполнения заданий высокого уровня сложности. Как правило, тестируемые приступают к решению 3–4 задач с развёрнутым ответом, правильно записывают основные законы и формулы и не испытывают серьёзных математических трудностей при решении систем уравнений. Поэтому им обычно удаётся довести до правильного ответа решения задач по механике (С1), молекулярной физике (С2) или электродинамике. Однако они предпочитают либо вообще не приступать к решению задач с нестандартной формулировкой (например, на дифракцию электронов или взаимодействие электронов с атомом), либо бросают решать их на полпути в силу непонимания описанных процессов.

При отличном уровне подготовки средняя выполняемость заданий такова: 88% для заданий с выбором ответа; 77% для заданий с кратким ответом; 62% для заданий с развёрнутым ответом. Характерно выполнение (выше 60%) в среднем четырёх из шести заданий части 3. По сравнению с предыдущей группой они не просто имеют объём знаний, но полноценно их усвоили, могут свободно оперировать понятийным аппаратом школьного курса физики, понимают особенности протекания достаточно сложных процессов и явлений. Особенно это касается задач с нетрадиционными формулировками, при решении которых необходимо представить себе происходящие процессы и явления, а не только вспомнить разбиравшиеся на уроках.

В заключение приведём примеры типичных заданий и их выполняемость группами с разной подготовкой.

• Базовый уровень. На рисунке изображено расположение двух неподвижных точечных электрических зарядов +2q и +q и обозначены три точки А, В и С. Модуль вектора напряжё нности суммарного электрического поля этих зарядов имеет:

1) наибольшее значение в точке А;

2) наибольшее значение в точке В;

3) наибольшее значение в точке С;

4) одинаковые значения во всех трёх точках.

Выполняемость

• Повышенный уровень. Электромагнитная волна от некоторого источника распространяется в бензоле, при этом длина волны составляет 1,2 мм. Определите период колебаний источника. Показатель преломления бензола 1,5. Ответ выразите в пикосекундах (10^–12 с). (Ответ: 6.)

Выполняемость

• Высокий уровень. Полый металлический шарик массой 2 г подвешен на шёлковой нити и помещён над положительно заряженной плоскостью, создающей однородное вертикальное электрическое поле напряжённостью 10⁶ В/м. Шарик имеет положительный заряд 10^–8 Кл. Период малых колебаний шарика 1 с. Какова длина нити? Ответ в сантиметрах (см) округлить до целых. (Ответ. 38.)

Выполняемость