Д.А.ИВАШКИНА ,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
Поэтапное обучение обработке
экспериментальных данных
1. Обучение открытию закона на
эмпирическом уровне познания
Если внимательно рассмотреть
обобщённые схемы различных видов деятельности
учащихся на уроках физики [1], то становится ясным,
что экспериментальный метод решения
познавательных задач в том или ином виде
встречается в большинстве видов деятельности,
связанных с созданием элементов физического
знания на эмпирическом уровне познания:
получение закона и научного факта, введение
новой физической величины (ФВ), создание понятия
«физическая величина», создание понятия
«физический объект». При обучении теоретическим
методам познания [2] тоже необходим проверочный
эксперимент, подтверждающий предсказания,
являющиеся следствием выдвинутых гипотез.
Однако достаточно серьёзная обработка
результатов эксперимента требуется лишь при
выполнении деятельности по выявлению устойчивых
связей и отношений между ФВ (построение графика с
указанием погрешности и формулирование вывода о
виде зависимости), а также при нахождении
значения физической величины с помощью
эксперимента методом косвенных измерений с
оценкой погрешности результата. Задачи первого
типа встречаются при открытии закона на
эмпирическом уровне познания или при проверке
предположения о виде зависимости между ФВ,
сделанного на теоретическом уровне познания.
Задачи второго типа – при установлении научного
факта на эмпирическом уровне познания или при
решении практических и исследовательских задач.
Общая логическая схема деятельности
по «открытию» законов, а также достаточно полный
перечень познавательных задач, которые можно
решать экспериментально на уроках физики в 7–11-м
классах, приведены в электронной версии статьи
на сайте газеты «Физика» № 18/07 ( https://fiz.1sept.ru ) в рубрике
«Дополнительные материалы».
2. Обучение оценке абсолютной
погрешности прямых измерений и использованию
погрешности для сравнения различных значений ФВ
и построения графиков (7–8-й классы)
Вопрос о необходимости вводить
понятие абсолютной погрешности должен решить
сам учитель. На мой взгляд, слово «абсолютная» на
этом этапе не осознаётся учащимися, т.к. они ещё
не знают, что существует относительная
погрешность. Его можно ввести при изучении
относительной погрешности как дополнительную
характеристику к уже хорошо усвоенному понятию
погрешности.
2.1. Системы познавательных задач,
при решении которых можно обучать основам оценки
абсолютной погрешности результата прямых
измерений. Чтобы понять смысл введения
погрешности измерения, нужно самостоятельно
прийти в своей деятельности на уроке к
необходимости измерять с учётом погрешности.
Каждый учитель может составить план проведения
экспериментов с указанием познавательных задач
(ПЗ) исходя из матобеспечения кабинета и уровня
подготовки класса.
Важным видом деятельности, в ходе
которой ученики убеждаются в необходимости
указания погрешности, является построение
графиков для выяснения вида зависимости одной ФВ
от другой. Ведь в большинстве случаев через
экспериментальные точки невозможно провести
гладкую кривую. Вот здесь и выручает погрешность.
Через «кресты» погрешностей можно провести не
просто кривую, а часто и прямую, проходящую через
начало координат, что означает прямо
пропорциональную зависимость между
исследуемыми величинами. Программа для 7-го и 8-го
классов предлагает много законов с такой
зависимостью между величинами. Например, они
исследуются в работах «Разработать метод
сравнения силы с единицей силы, заданной с
помощью единичного удлинения пружины», «Зависит
ли разность температур, на которую нагревается
тело, от количества теплоты, сообщённого ему?
Каков вид этой зависимости?».
Определённая и хорошо продуманная
логика требуется при введении сил и методов
их измерения. Я поступала так. Сначала
рассматривала вопрос о взаимодействии тел.
Поскольку одно тело может воздействовать на
другое с различной интенсивностью, требуется
ввести ФВ, характеризующую взаимодействие. Но
какое воздействие выбрать в качестве меры или
эталона? По-видимому, надо изучить, какие виды
взаимодействий вообще существуют, чтобы потом
выбрать то, которое позволит нам ввести единицу
новой ФВ. После изучения различных видов
взаимодействий я подводила учащихся к тому, что
измерять силу упругости можно с помощью упругих
свойств пружины. Так, введя единичное удлинение,
мы тем самым вводим единицу силы.
А как найти удлинение, соответствующее
единице силы для другой пружины? Известно, что
тело покоится или движется по инерции, если
действие на него других тел компенсируется.
Скомпенсировав действия на тело эталонной и
неизвестной пружины, мы можем ввести единичное
удлинение.
Следующий вопрос («А как сравнить
силы?») учащиеся решают легко: тело начинает
движение в сторону большей силы. А как теперь
получить силу в два, три и т.д. раз бoльшую, чем
единица силы? Подействовать на тело эталонной
пружиной в одном направлении, а в
противоположном – двумя, тремя и т.д. пружинами с
отмеченными единичными удлинениями. При этом
проследить, чтобы эти несколько пружин
прикладывались не последовательно, а в одной
точке, и действовали строго в одном направлении.
Удобно воспользоваться обычными школьными
динамометрами с заклеенной шкалой. Так
производится градуировка эталонной пружины.
При этом учащиеся сами замечают, что
удлинения, соответствующие двум, трём и т.д.
единицам силы, кратны друг другу: расстояния
между отметками кажутся одинаковыми. Эта догадка
является гипотезой, которая и проверяется
построением графика зависимости силы упругости
(в единицах силы) от удлинения пружины (в
сантиметрах). Таким образом, этот закон
«открывается» попутно, без постановки
познавательной задачи.
Закон Архимеда и
соответствующее количественное соотношение
между ФВ (формулу) можно вводить как на
эмпирическом, так и на теоретическом уровне
познания. Эмпирический путь дольше, т.к.
возникает очень много гипотез, от каких ФВ может
зависеть выталкивающая сила. Все они требуют
экспериментальной проверки. В случае
теоретического пути учитель помогает учащимся
получить формулу (в качестве мотивации могут
быть использованы задача, проблема, наводящие
вопросы и т.д.), а затем предсказанные зависимости
проверяются экспериментально (например, как FА
зависит от 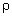 т,
т,
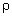 ж, Vт.
В этом случае ПЗ формулируются так:
«Действительно ли выталкивающая сила,
действующая на тело, погружённое в жидкость,
прямо пропорциональна плотности жидкости?»
ж, Vт.
В этом случае ПЗ формулируются так:
«Действительно ли выталкивающая сила,
действующая на тело, погружённое в жидкость,
прямо пропорциональна плотности жидкости?»
Пояснения требуют и работы по теплоте
и электричеству в 8-м классе. При введении новой
ФВ «Количество теплоты» трудность состоит в том,
что мы не можем её измерить, хотя рассказать об
опытах Джоуля, на мой взгляд, необходимо. Можно
предложить ребятам самим придумать, как измерить
количество теплоты, а затем рассказать об
истории этого вопроса. При решении первой ПЗ о
зависимости температуры от количества теплоты
следует обсудить проблему, как сравнивать
количества теплоты, если мы не можем их измерить.
На мой взгляд, проще всего является
предположение о том, что спиртовка за равные
промежутки времени даёт равные количества
теплоты. Тогда решается ПЗ о зависимости
изменения температуры от времени нагрева.
Количество теплоты, выделяемое при сгорании
топлива, оценивается по температуре нагреваемой
при этом воды, а в дальнейших работах (при
изучении плавления и парообразования) можно
оценивать количество теплоты по массе
сгоревшего топлива или по времени горения
спиртовки.
При изучении законов постоянного
тока трудность при «открытии» закона Ома
состоят в том, что в стандартном лабораторном
оборудовании отсутствуют источники питания,
способные давать различные значения напряжения,
а реостат изучается после введения ФВ
«сопротивление», т.е. уже после изучения закона
Ома. Я вышла из этого положения так. При введении
ФВ «сила тока» возникают вопросы: от чего зависит
сила тока? может ли сила тока принимать различные
значения в одной и той же цепи? Затем делается
работа по измерению силы тока в различных точках
последовательной цепи. Она служит и цели
обучения сравнению экспериментальных значений с
применением погрешности.
Изучая напряжение, ученики сами
предлагают измерить напряжение на различных
участках последовательной цепи. Во-первых, им
интересно узнать, как соотносится напряжение на
различных участках цепи с напряжением на
источнике тока (последнее мы измеряем при
самостоятельном «изготовлении» его с помощью
различных электродов в электролитической ванне).
Во-вторых, зная, что существует закон для силы
тока при последовательнм соединении, они
предполагают, что он должен существовать и для
напряжения. Новым оказывается и тот факт, что
напряжение на проводнике при замкнутом ключе
равно нулю. Становится ясным, почему некоторые
проводники называют резисторами, а другие –
просто проводниками. В общем, изучение
последовательного соединения до закона Ома
полезно во многих отношениях.
При таком подходе, изучая зависимость
силы тока от напряжения, учащиеся сами
предлагают эксперимент, в котором резистор
включается в цепь последовательно с другими
элементами (спиралью, лампочкой, другими
резисторами и т.д.). При удалении каждого из этих
дополнительных элементов напряжение на
резисторе изменяется, следовательно, изменяется
и сила тока. Таким образом, каждая группа (пара)
школьников имеет возможность построить график и
убедиться в том, что зависимость силы тока от
напряжения – прямая. При этом нет нужды
проводить многократные опыты, т.к. у каждой
группы свои коэффициенты пропорциональности, и
можно сделать вывод, что коэффициент
пропорциональности определяется свойствами
проводника.
При изучении оптических явлений
можно изучить зависимость угла отражения от угла
падения (например, с помощью лабораторного
оборудования лаборатории «L-микро»).
Дальнейшее зависит от уровня класса. В классах
физматпрофиля мы получаем зависимость синуса
угла преломления от синуса угла падения.
Поскольку находить погрешность синуса учащиеся
не умеют, в таблицу синусов я внесла погрешность
синуса для каждого значения угла для нескольких
значений погрешности угла (такую таблицу легко
сделать в Excel). В других классах отражение и
преломление изучаются в демонстрационном
эксперименте. Но к концу года ученики уже
практически владеют деятельностью по открытию
закона. Поэтому такой вид «упрощённого»
эксперимента можно сопроводить рассказом о
многочисленных экспериментах древних,
предшествовавших выводу законов геометрической
оптики.
Подробнее о системах познавательных
задач для открытия законов в 8-м классе
сообщается в [3].
2.2. Основные понятия и операции с
погрешностями. В табл. 1 приведены основные
понятия, которые должны быть усвоены учащимися
на первом этапе обучения действиям с
погрешностью.
Таблица1

Двумя последними действиями учащиеся
овладевают на уроках математики, а на уроках
физики лишь «вспоминают» эти действия и учатся
их использовать при решении физических задач.
Первые же два действия – новые для учащихся, и
поэтому для их усвоения нужно провести
специальные уроки с выполнением серии
упражнений [1, 4].
Впервые вопрос о погрешности
измерения возникает при введении понятия
«Физическая величина» в 7-м классе. При
обсуждении различных свойств физических тел
появляется потребность сравнить
«интенсивность» данного свойства у различных
тел, например, протяжённость двух тел в
пространстве. Результат измерения зависит от
тела, выбранного мерой. Для удобства измерений
вводится шкала, а с ней и понятия «деление шкалы»,
«числовая отметка шкалы», «градуирование шкалы
измерительного прибора». Здесь можно ввести
такие понятия, как «интервал округления»: при
сравнении длины двух почти одинаковых отрезков
необходимо уменьшить интервал округления
значений их длины. На этом же уроке обсуждаются
другие измерительные приборы и предлагается
изготовить дома самодельную мензурку для
измерения объёма жидкости в столовых ложках.
На следующем уроке при обсуждении
изготовленных мензурок вводится понятие «цена
деления шкалы прибора». Затем учащиеся измеряют
один и тот же объём жидкости различными
мензурками и приходят к выводу, что шкалы на
мензурках изготовлены также с определённой
погрешностью. Наличие инструментальной
погрешности проверяется на примере ученических
линеек. Ребята приходят к необходимости
учитывать каким-то образом качество
измерительного прибора и проведённых с его
помощью измерений. Учитель предлагает записать
результат с учётом погрешности измерения. На
последующих уроках проводится обучение снятию
показаний с приборов с учётом погрешностей.
Следующая встреча с понятием
погрешности происходит при выполнении
лабораторной работы «Определение размеров
молекул методом рядов». Учащиеся сами замечают,
что изображения различных молекул неодинаковы, и
приходят к выводу, что нужно найти среднее
значение «длины» молекулы. Но насколько можно
верить полученному значению? Может, надо
поделить на количество молекул в ряду и
погрешность? При делении возникает вопрос: стоит
ли округлять полученное число с большим числом
десятичных знаков? Здесь логично вспомнить об
интервале округления и округлить число. При этом
учитель может объяснить, что погрешность
округления должна быть не больше погрешности
измерения. Понимание необходимости округления
очень важно при решении задач. Поэтому к
погрешности вычислений с помощью калькулятора и
округления можно будет вернуться при решении
первых задач. Это важно, т.к. если не обсудить с
учащимися вопрос об округлении и его
необходимости на первых же уроках, вопросы «А
нужно округлять?» будут задаваться ещё очень
долго.
Опыт показывает, что не следует
вводить сразу много понятий на одном уроке, а
каждое введённое понятие необходимо закреплять
на ближайших уроках. Каждый вид деятельности
вводится на нескольких уроках (подготовительный
этап), затем составляется план действий для
данного вида деятельности (этап обобщения), после
чего учащиеся действуют по составленному плану
самостоятельно (этап конкретизации). Например, с
деятельностью по нахождению абсолютной
погрешности измерений учащиеся знакомятся
(«придумывают, как это сделать») при измерении
длины тела, объёма жидкости с помощью мензурки,
при определении размеров тела методом рядов.
Затем следует урок обобщения для этого вида
деятельности, а конкретизируется и применяется
составленный план действий по определению
погрешности в экспериментах по открытию законов
равномерного движения (измерение пути и времени),
пропорциональности массы однородного тела его
объёму, законов для сил (измерение сил, масс,
удлинения пружины) и т.д. Эксперименты по
открытию законов приводят к необходимости
строить график с учётом погрешности, а после
обобщения накопленного при открытии двух-трёх
законов опыта учащиеся закрепляют свои умения в
дальнейших экспериментах по открытию законов в
курсе 7-го и 8-го классов. Сравнение физических
величин с учётом погрешности встречается уже при
первых измерениях, но обобщение этой
деятельности и этап конкретизации её удобно
провести в курсе 8-го класса, при изучении законов
последовательного и параллельного соединений.
Особого обсуждения заслуживает вопрос
об определении абсолютной погрешности при
определении массы. Способ определения
погрешности через сумму погрешностей каждой
используемой гири по погрешности, даваемой
весами [1, 6], очень трудоёмок даже для
старшеклассников. Кроме того, точность измерения
массы на лабораторных весах и так неоправданно
велика.
Поясню на примере. Допустим, значение
массы тела, измеренное на весах, составляет 55 г 270
мг, и последняя добавленная на чашку весов гирька
имеет массу 10 мг. При вычислении погрешности
массы с учётом систематической погрешности
весов и разновесов и погрешности отсчёта [6] мы
получаем абсолютную погрешность массы 132 мг. При
округлении оставляем две значащие цифры, т.к.
первая значащая цифра 1:  m = 0,13 г. Окончательный результат m
= (55,27 ± 0,13) г. Относительная погрешность измерения
массы 0,2%.
m = 0,13 г. Окончательный результат m
= (55,27 ± 0,13) г. Относительная погрешность измерения
массы 0,2%.
Ясно, что если конечной целью
эксперимента является определение какой-либо
величины косвенным путём с измерением
нескольких величин, то такая точность измерения
просто бессмысленна. На мой взгляд, в 7-м классе
следует объяснить детям, что инструментальная
погрешность измерения массы очень мала, и её
можно не учитывать. А погрешность отсчёта можно
найти как половину интервала округления,
оставляя все значащие цифры до единиц граммов
включительно. Результат в нашем случае окажется
(55,0 ± 0,5) г с относительной погрешностью 0,9%.
Погрешность ненамного увеличилась, а процесс
расчёта стал гораздо проще.
3. Обучение оценке абсолютной и
относительной погрешностей косвенных измерений
(9-й класс)
Если необходимость введения понятия
«абсолютная погрешность» и использование его
для сравнения значений величин и построения
графиков достаточно прозрачна и не раз
обсуждалась в литературе [1, 2, 7], то необходимость
введения понятия «относительная погрешность»
является неочевидной порой даже для учителей
физики.
3.1. Система познавательных задач,
при решении которых можно обучать учащихся
основам оценки абсолютной погрешности
результата косвенных измерений. Если
обучение экспериментальному методу проводилось
с 7-го класса, то в 8-м учащиеся уже владеют
основными действиями по планированию
эксперимента, элементарной обработке
результатов эксперимента (построение графика
зависимости, сравнение значений величин). При
изучении механики впервые достаточно
систематически начинает применяться
теоретический метод познания [2, 8]. И здесь
эксперимент должен служить для проверки
теоретических предсказаний. После построения
уравнений движения для равноускоренного
движения (исходя из простейшей математической
модели равномерного изменения скорости)
необходимо проверить, действительно ли тела
могут двигаться по этим законам.
Объектами изучения могут служить:
тело, скатывающееся по наклонной плоскости; тело,
движущееся по горизонтальной плоскости под
действием груза, привязанного к нити,
перекинутой через блок; свободно падающее тело (с
определением ускорения свободного падения);
тело, брошенное горизонтально. Таким образом,
система задач может быть определена в
зависимости от комплектации кабинета.
Если понятие силы вводилось в 7-м
классе достаточно строго (см. п. 2.1.), то в 9-м классе
учащимся можно предложить определить
коэффициент пропорциональности в задачах,
которые выполнялись ранее при «открытии»
законов для силы тяжести, силы упругости и силы
трения, см. далее п. 3.5.
3.2. Понятия систематической и
случайной погрешностей и метод уменьшения
случайной погрешности. К необходимости
проводить многократные измерения учащиеся
приходят сами, если при проведении эксперимента
они видят, что результаты сильно отличаются друг
от друга (прежде всего в задачах по кинематике),
например, при измерении времени методом
совпадений (ЛР № 1 [8]). Ещё очевиднее наличие
случайной погрешности в работе «Изучение
движения тела, брошенного горизонтально».
Ученики сами предлагают произвести опыт много
раз и взять среднее значение дальности полёта. Но
возникает вопрос: как оценить погрешность? Может,
как среднее арифметическое суммы отклонений
(абсолютных значений отклонения)? А есть ещё и
погрешность каждого измерения.
И здесь учитель должен обобщить все
мнения, объяснив, что погрешности эти имеют
разную природу. Погрешности, определяемые
способом измерения (инструментальная
погрешность, погрешность отсчёта), невозможно
уменьшить. Можно лишь выбрать другой способ
измерения. Эти погрешности носят название систематических.
Погрешности, определяемые случайными
причинами (движение воздуха, колебания
установки и т.д.), носят название случайных и
могут быть уменьшены путём многократных
измерений. Поэтому, чем больше опытов, тем меньше
среднее отклонение (среднее арифметическое
абсолютных значений отклонений от среднего
значения величины) и тем точнее результат.
Продолжение см. в № 19/07
![]() т,
т,
![]() ж, Vт.
В этом случае ПЗ формулируются так:
«Действительно ли выталкивающая сила,
действующая на тело, погружённое в жидкость,
прямо пропорциональна плотности жидкости?»
ж, Vт.
В этом случае ПЗ формулируются так:
«Действительно ли выталкивающая сила,
действующая на тело, погружённое в жидкость,
прямо пропорциональна плотности жидкости?»