В последнее время в СМИ всё чаще появляются статьи и сообщения, которые иначе чем антинаукой назвать невозможно. Наиболее распространены случаи, когда автор использует терминологию физики, совершенно не понимая, о чём, собственно, идёт речь. Примером может служить совершенно очаровательный пассаж: «Наши приборы зафиксировали излучение неизвестной природы». Единственное, что можно сказать, что приборы были неисправны. Ведь каждый прибор конструируется и изготавливается так, чтобы фиксировать какую-то известную величину. Если он фиксирует что-то неизвестное, то он врёт.
В современной науке основополагающим является принцип, что новая теория должна объяснять всё, что объясняет известная нам теория, и что-то из того, что старая теория не могла объяснить, и предсказывать новые эффекты, проверяемые на опыте. Так, квантовая механика возникла лишь тогда, когда существовавшая электродинамика Максвелла не смогла объяснить, почему остывшая печь не излучает ультрафиолетовых волн и почему спектр водорода состоит из чёткой системы отдельных линий. Теперь каждый раз, включая телевизор или читая эту статью (она набрана на компьютере), вы получаете ещё одно доказательство правильности квантовой механики (изобретение транзистора – основы схем телевизора и компьютера – стало возможным только на основе квантовой механики).
Общая теория относительности давно подтверждена самыми эффектными опытами: полёты космических аппаратов ВЕГА (проект «Венера–Галлей»), «Вояджер» (два космических аппарата, пролетевшие мимо Юпитера, Сатурна, Урана и Нептуна) стали триумфом и этой теории, на основе которой рассчитывались траектории космических аппаратов, и квантовой механики, на основе которой создавалось оборудование.
Авторы антинаучных статей делятся на две категории. Первая (сравнительно безопасная) – люди просто самоуверенные и плохо знающие современную науку. Их теории легко опровергаются и особого вреда не наносят. Вторые – жулики, которые стремятся получить деньги для продолжения разработки своих теорий. Часто журналисты, не знающие физику даже в объёме средней школы, принимают за истину явное жульничество. Так, однажды во вполне респектабельной «Российской газете» появилась статья, в которой рассказывалось о замечательном опыте, проведённом в присутствии журналиста. Во время этого опыта масса прибора уменьшилась на 26 г. На этом основании его автор (поддержанный журналистом) просил для проведения дальнейших исследований и создания невероятно мощного источника практически даровой энергии всего 200 000 долл. Совершенно очевидно, что 200 000 не дадут, но 2000 могут и дать. Журналисту достаточно было заглянуть в любой школьный учебник физики или в «Энциклопедический словарь», чтобы подсчитать на калькуляторе, что при исчезновении 26 г массы выделится энергии, как при взрыве примерно 50 000 мегатонных водородных бомб. Дальше говорить об этом «открытии», пожалуй, не стоит.
В 50-х гг. прошлого столетия в печати
появились сообщения об очередном «гениальном»
изобретении: речь шла о космическом лифте
Ю.В.Арцутанова. Сама по себе идея такого лифта не
противоречит законам механики, но, как всегда,
дьявол прячется в деталях. Коротко идея
Ю.В.Арцутанова состоит в том, что суточный
спутник, т.е. спутник, период обращения которого
строго равен суткам, соединяется канатом с тем
местом на экваторе Земли, над которым висит этот
спутник. Далее по канату можно поднимать груз,
используя другой груз, который свободно
поднимается вверх, движимый центробежной силой.
Таким образом, б
льшая часть энергии, требуемой для
запуска космических аппаратов, может быть
заимствована из энергии вращения Земли. Идея эта
популяризируется многими авторами, в частности,
в интернете. К сожалению, никто из авторов не
подвергает идею Ю.В.Арцутанова критическому
рассмотрению, даже не пытается сколько-нибудь
подробно рассмотреть основные аспекты самой
идеи с точки зрения механики. В настоящей статье
мы рассматриваем некоторые детали, связанные с
осуществлением этого заманчивого проекта.
Деталь первая – системы отсчёта. Рассмотрение задачи возможно в одной из двух систем отсчёта (СО). Сторонники Ю.В.Арцутанова предпочитают рассматривать задачу в неинерциалоной системе отсчёта (НИСО), вращающейся вместе с Землёй. Обычно же нужно рассматривать задачу в инерциальной системе (ИСО). Мы будем пользоваться обеими системами, всегда оговаривая, в какой в настоящий момент работаем.
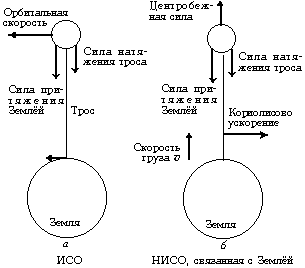
Рис. 1. Суточный спутник над Землёй
Описание лифта в инерциальной системе
(рис. 1, а) заключается в том, что спутник
движется, обращаясь вокруг Земли за 24 ч. В этом
случае он непрерывно «висит» над одной точкой
земного экватора. Скорость же точек лифта
меняется от 460 м/с на поверхности Земли до
3170 м/с на суточной орбите. В этой ИСО свободно
падает и находится в состоянии невесомости. Трос
лифта тоже движется вокруг оси Земли, и каждая
его точка обладает скоростью орбитального
движения, равной 
= 
r (r –
расстояние от центра Земли, – орбитальная скорость).
В НИСО (рис. 1, б) к спутнику
приложена центробежная сила. В системе
появляется новая величина – кориолисово
ускорение aк = 2[
].
(Это ускорение объясняет, в частности, и тот факт,
что в Северном полушарии реки подмывают свой
правый берег, а в Южном – левый.) Направление
ускорения определяется направлением движения
тела. Оно одинаково для всех тел независимо от их
массы. Так, на рис. 1, б изображено
кориолисово ускорение при подъёме тела, при
спуске оно имеет противоположное направление. В
рассуждениях авторов проекта это ускорение
отсутствует.
Деталь вторая – канат.
Суточный спутник движется на расстоянии
36 600 км от поверхности Земли со скоростью
около 3170 м/с. Канат космического лифта должен
быть такой же длины. Для простоты расчётов
примем, что наш канат представляет собой тонкую
стальную проволочку площадью поперечного
сечения 1 мм2. Поскольку нас интересует,
когда оборвётся канат под собственным весом, то
заметим, что результат не зависит от площади
поперечного сечения. Напряжение 
= F/S, где S
– площадь поперечного сечения, в данном случае
не зависит от площади, поскольку с увеличением
площади увеличивается в той же пропорции и сила
(в данном случае – вес проволоки).
Оценим массу стальной проволоки: M = 
SL. Если = 7,8 • 103 кг/м3
– плотность стали, то масса 1 км проволоки
составляет 7,8 кг, а 36 000 км – 281 т.
Предельную длину проволоки определим,
разделив предельное напряжение на вес проволоки:
Fmax = S = gSLmax. Для стали получается = 13 • 107 Н/м2.
Подставив в эту формулу известные значения,
получим, что предельная длина троса составит 1,7
км. А нужно 36 000 км, т.е. примерно в 2500 раз больше.
Конечно, можно уменьшить эту цифру раз в 10, может
быть, в 20, но большего достигнуть, по-видимому, не
удастся.
Авторы, пропагандирующие космический лифт, предлагают сплести канат из углеродных нанотрубок. Действительно, прочность таких трубок огромна, но пока никто не смог получить трубку длиннее 2 см. А нужно хотя бы 1 м. Правда, заплатить за такой канат нужно будет очень и очень много, по сравнению с такой стоимостью 1 млрд долл. кажется просто копейками. Отметим, что прочность каната не будет определяться прочностью нитей. При всех обстоятельствах главным фактором является не прочность нанотрубок, а сила сцепления между ними. Очень маловероятно, что прочность каната возрастёт в 1000 раз, а его масса уменьшится раза в два. Так что даже возможность создания такого каната представляется весьма и весьма сомнительной.
Поскольку космический лифт имеет смысл вообще только тогда, когда он постоянно связывает спутник и определённую точку на Земле, очевидно, что канат должен быть направлен строго по радиусу Земли, значит, угловая скорость любой его точки должна быть строго постоянной (7,39 • 10–5 c–1).
Деталь третья – установка каната. Поднимать канат с поверхности Земли невозможно, попробуем опустить его со спутника. Представим себе, что первая трудность преодолена, канат создан и поднят на большой суточный спутник. Остаётся только спустить его к Земле и закрепить в выбранной точке, над которой висит спутник? Ничего подобного. Всё гораздо сложнее.
Спутник на орбите находится в состоянии невесомости. Ничего не весит та часть каната, которая примыкает к спутнику или находится внутри него. Потому он не будет двигаться вниз (нет веса), придётся опускать его насильно. Справиться с этим достаточно легко, прицепив к концу каната жёсткий стержень, который выведет канат в область, в которой сила тяготения, пусть очень ненамного, но превышает центробежную силу. Затем, опускаясь, трос выйдет из зоны невесомости и начнёт тянуть оставшуюся часть, постепенно увеличивая скорость. Так будет установлен основной элемент космического лифта.
Однако дело обстоит существенно иначе, гораздо сложнее. Обратите внимание на то, что в инерциальной системе нет центробежного ускорения, вернее, оно есть, но приложено не к спутнику, а к центру Земли. Спутник движется по круговой орбите просто потому, что ускорение, которое придаёт ему сила тяжести, равно ускорению, с которым он движется по окружности. Благодаря этому спутник находится в состоянии невесомости.
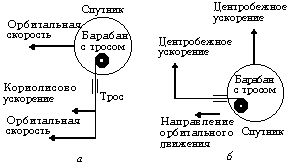
Рис. 2. Спуск троса на Землю (НИСО)
Установка (или спуск по направлению к Земле) троса встретится с большими трудностями. Придётся выталкивать трос, пользуясь его жёсткостью (рис. 2, а; НИСО).
Когда выдвинутая часть троса станет достаточно большой, сработает «эффект хлыста» (заключающийся в том, что длинный стержень легче согнуть, чем короткий) – трос начнёт изгибаться. Связано это с тем, что нижний конец троса (стержня) движется по более короткой орбите и обгоняет спутник. В НИСО это объясняется наличием кориолисова ускорения. Если кориолисово ускорение не компенсировать, то оно создаёт силу, действующую на трос, трос отклоняется от вертикали, возникает центробежная сила. Но спутник ничего не весит, он в состоянии невесомости. Поэтому спутник начнёт поворачиваться (2, б; НИСО). В результате трос не будет опускаться к Земле, а вытянется по суточной орбите.
Центробежное ускорение полностью с большим запасом компенсирует приливное (обусловленное разностью силы тяжести на разных высотах), и движение троса определяется центробежным и кориолисовым ускорениями. Очень трудно представить, как можно последнее компенсировать в каждой точке троса, учитывая, что трос опускается, а кориолисово ускорение в каждой точке пространства (а не в каждой точке троса) действует постоянно. Без компенсации же кориолисова ускорения нечего и думать о спуске троса. Надо сказать, что такая компенсация потребует затраты немалого количества энергии. Но не будем слишком придирчивыми. Такие мелочи, как проблему прикрепления троса к спутнику и опасность обрыва (которая более чем реальна), что может принести немало бед, мы оставляем без рассмотрения.
Но, даже если такая компенсация и удастся, то сразу же возникнет ещё одна трудность. Если мы действительно хотим опустить трос, то нужно учитывать, что по мере опускания вес троса увеличивается, что приводит ко всё большей скорости опускания. Если не принимать никаких мер, то трос упадёт на Землю со скоростью 3000 м/с. Единственный способ тормозить трос – это создание силы трения. Но представьте себе, с какой силой нужно давить на тормозные колодки, чтобы удержать трос весом несколько сотен тонн. Что после этого случится с тросом? Здесь нужны подробные расчёты, которые должны сделать специалисты. Но простая прикидка показывает, что требуемая сила просто раздавит трос.
По мере опускания троса увеличивается и сила его натяжения. Сила натяжения приложена к спутнику. Именно она удерживает трос от падения. Дополнительный вес можно рассматривать как усиление силы тяжести. Компенсировать его может только центробежное ускорение, которое растёт при постоянном периоде обращения (или постоянной угловой скорости) пропорционально радиусу орбиты. Простые оценки показывают, что для компенсации веса троса, что даёт возможность двигаться по суточной орбите, необходимо поднять спутник приблизительно на высоту 18 радиусов Земли, т.е. примерно на 102 000 км.
Значит, придётся увеличивать радиус орбиты или, другими словами, переводить спутник на более высокую орбиту. Но это возможно, только направив спутник на промежуточную орбиту. Период обращения на промежуточной орбите больше, чем на круговой, и спутник, а значит, и трос, отклонится от вертикали, что немедленно приведёт к катастрофе. Вероятно, возможен такой подъём спутника, что он по-прежнему будет висеть над одной точкой поверхности Земли. Но найти, а затем осуществить такой способ очень трудно. Очень вероятно, что задача в принципе не имеет решения.
Отметим, что задача стабилизации троса очень сложна, и мы сделали только очень приблизительные оценки. Можно уверенно сказать, что более точные расчёты выявят множество дополнительных трудностей.
Деталь четвёртая – зачем? Теперь зададим основной вопрос: «А для чего это всё нужно?» Ответ авторов проекта: «Мы будем практически бесплатно выводить тяжёлые спутники на промежуточную круговую орбиту. собирать там тяжёлые космические аппараты и отправлять их в дальний космос. Мы получим даровой источник энергии за счёт энергии вращения Земли».
Даровой источник энергии, да ещё за счёт вращения Земли, это, конечно, очень и очень заманчиво. Вот только удастся ли получить энергию за счёт вращения Земли? Дело в том, что единственная сила, которая может в космическом лифте производить работу, это центробежная сила. Но эта сила никак не может изменить энергию вращения Земли по той простой причине, что центробежная сила и перемещение за счёт вращения Земли перпендикулярны друг другу. А в этом случае сила работы не совершает – это знает, или должен знать, любой школьник старше 7-го класса. Ни автору проекта, ни его апологетам это, по-видимому, неизвестно.
Но, скажете вы, ведь, когда тело поднимается, центробежная сила совершает работу. Это неверно. И это становится ясно, если вы перейдёте в ИСО. Для того чтобы тело поднималось, нужно увеличивать его скорость, перпендикулярную направлению движения. Но если сила перпендикулярна перемещению (скорости), то работы она не совершает. Наоборот, компенсируя кориолисово ускорение, мы совершим работу, равную работе, совершаемой при переводе поднимаемого тела с одной суточной орбиты на другую. Эта работа равна работе, совершаемой телом при своём разгоне (торможении) от скорости 500 м/с до 3100 м/с. Причём эту работу нужно будет совершать как при подъёме груза (разгон), так и при его опускании (торможение). То есть никакого выигрыша не будет, будут только потери. Но в этом случае сам космический лифт теряет какой-либо смысл.
Заключение
Итак, можно сказать, что сторонники и автор проекта могут не беспокоиться, что американцы украдут идею и построят космический лифт. Это связано с невероятными сложностями и совершенной бессмысленностью, поскольку доставка грузов космическим лифтом требует намного больше энергии, чем тратится при доставке того же груза традиционными космическими ракетами. А авторам можно порекомендовать: прежде чем публиковать сенсационный проект, самим сделать те простые оценки, которые мы сделали в настоящей заметке.
Для того, чтобы убедиться, что никакого космического лифта не может быть, достаточно взглянуть на него с Луны.
ДОПОЛНЕНИЕ РЕДАКЦИИ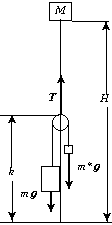 
Движение тел при рассмотрении космического лифта в любом техническом исполнении подчиняется закону сохранения энергии. Мы можем мысленно построить любую идеальную конструкцию лифта.
Предположим, что мы имеем сверхпрочные
идеальные канаты. Построим космический лифт в
соответствии с рисунком. Нижний конец каната
закреплён на Земле, другой конец каната – на
теле, вращающемся вокруг Земли на большой высоте H
с угловой скоростью , равной угловой скорости суточного
вращения Земли 7,4 • 10–5 с–1.
Масса тела M и его высота над Землёй H
должны обеспечить заданное натяжение каната T.
Закрепим на канате блок на высоте h, на
которую мы предполагаем доставить груз массой m.
Через блок пропустим второй канат и получим тали.
Груз можно поднимать, прилагая к свободному
концу этого каната силу mg, или подсоединить
противовес весом m*g, как это
делается в пассажирских лифтах. Оценим грубо
размеры космического лифта и его «преимущества».
Натяжение основного каната обусловлено центробежной силой инерции тела M:
T = MH2
и должно быть не меньше 2mg.
Таким образом, 
Примем M 
20m.
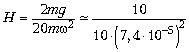= 1,8 • 108 (м) = 1,8 • 105 (км),
т.е. получим высоту, намного превышающую размеры Земли. Кроме того, необходимо обеспечить скорость тела M на орбите и сохранять её.
= H = 7,4 • 10–5 • 1,8 • 108 = 13,5 (км/с).
Таким образом, конструкция фантастическая. Чтобы воспользоваться противовесом, надо предварительно поднять его на высоту h! Так не проще ли непосредственно на эту высоту поднять полезный груз? Для подъёма следующей партии груза массой m вновь надо поднимать противовес. Идея Ю.В.Арцутанова предусматривает наличие вспомогательного груза, который также надо поднимать и опускать.
В данном примере приняты грубые приближения: не учитывается радиус Земли и изменение ускорения g с высотой. Величина Н оказывается равной половине расстояния до Луны, а Луна висит почти неподвижно. Однако нецелесообразность соединения Земли и Луны канатом очевидна.