Проф. С.И.ЛЕЖНИН, проф. О.Я.САВЧЕНКО,
проф. О.Ю.ЦВЕЛОДУБ,
СУНЦ НГУ, г. Новосибирск
Задачи приёмных экзаменов на
физическое отделение заочной школы СУНЦ НГУ
9-й КЛАСС
1. Опоздавший на автобус пассажир,
спустя 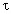 = 20 мин
после его отъезда из пункта А, сел в такси,
чтобы пересесть на этот автобус на следующей
остановке в пункте В. Такси обогнало автобус
в момент, когда он уже прошёл 2/3 пути от пункта А
до пункта В. Сколько времени tх
будет ждать пассажир автобуса в пункте В?
= 20 мин
после его отъезда из пункта А, сел в такси,
чтобы пересесть на этот автобус на следующей
остановке в пункте В. Такси обогнало автобус
в момент, когда он уже прошёл 2/3 пути от пункта А
до пункта В. Сколько времени tх
будет ждать пассажир автобуса в пункте В?
Решение
Обозначим расстояние между пунктами А
и В через L, время движения автобуса
между пунктами через t, а скорость такси
через uт. По условию задачи, проезд на
такси между пунктами занял на 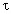 + tх меньше времени: uт(t
–
+ tх меньше времени: uт(t
– 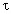 – tх)
= L.
– tх)
= L.
Автобус за время 2t/3 прошёл путь 2L/3,
а такси этот же путь – на 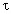 быстрее: uт =
быстрее: uт = 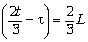 .
.
Решая совместно уравнения, получим:
3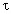 /2 =
/2 = 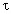 + tx, или tх
=
+ tx, или tх
= 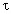 /2 = 10 мин.
/2 = 10 мин.
Ответ можно получить сразу: если 2/3
пути такси прошло быстрее на 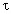 , то оставшуюся треть – на
, то оставшуюся треть – на 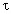 /2 (столько и надо
ждать).
/2 (столько и надо
ждать).
2. На автомобиле определяют с помощью
звукового сигнала расстояние до поста ГАИ. Какое
расстояние L было до поста в момент испускания
звукового сигнала, если после отражения от будки
его приняли через t0 = 12 с? Скорость
звука с = 325 м/с, скорость автомобиля u = 90
км/ч.
было до поста в момент испускания
звукового сигнала, если после отражения от будки
его приняли через t0 = 12 с? Скорость
звука с = 325 м/с, скорость автомобиля u = 90
км/ч.
Решение
За время t0 автомобиль
проехал расстояние ut0. Поэтому полный
путь, пройденный звуковым сигналом, равен L + L
– ut0. Следовательно, сt0 = 2L
– ut0.
С учётом того, что 90 км/ч = 25 м/с:
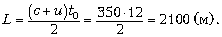
3. Пустой толстостенный стеклянный
стакан массой m = 100 г плавает в сосуде
сечением S = 0,05 м2 с водой. После того
как стакан утопили, уровень воды в сосуде
опустился на h = 1 мм. Найдите плотность
стекла 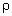 с.
Плотность воды
с.
Плотность воды 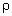 в
= 1000 кг/м3.
в
= 1000 кг/м3. 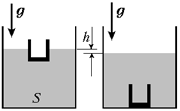
Решение
Обозначим объём стекла Vс = m/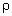 с, а объём
вытесненной плавающим стаканом воды V.
Сначала сила Архимеда равна весу стакана: FА
=
с, а объём
вытесненной плавающим стаканом воды V.
Сначала сила Архимеда равна весу стакана: FА
= 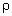 вVg = mg
=
вVg = mg
= 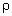 сVс
g. Отсюда V = Vс
сVс
g. Отсюда V = Vс 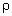 с/
с/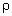 в.
в.
Так как объём воды в сосуде не
изменяется, то Sh = V – Vс.
Решая совместно все приведённые соотношения,
получим:
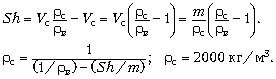
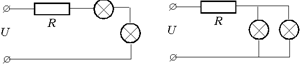
4. Две одинаковые лампочки и один
резистор сопротивлением R подсоединили к
источнику напряжения U двумя способами, как
показано на рисунках. В обоих случаях накал
лампочек был одинаков. Ток какой силы I
протекает через одну лампочку?
Решение
Если накал лампочек одинаков, то
одинакова и сила тока I, текущего через
каждую лампочку. Пусть сопротивление включённой
лампочки Rл. При последовательном
соединении резистора и лампочек:
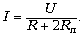
При параллельном соединении лампочек
полный ток равен 2I (через каждую лампочку по I).
При этом их суммарное сопротивление равно Rл/2,
а полное сопротивление цепи R + Rл/2:
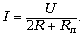
Решая совместно оба уравнения,
получим:
Rл= R; I = U/(3R).
10-й КЛАСС
1. См. задачу 2 для 9-го класса.
2. На тело массой m, расположенное
на горизонтальном шероховатом столе, действует
горизонтальная сила F так, что оно
движется с ускорением. После того как силу
увеличили в 2 раза, ускорение стало в 3 раза
больше. Определите коэффициент трения, если F
= 49 H, m = 10 кг, g = 9,8 м/с2.
Решение
Запишем 2-й закон Ньютона для обоих
случаев:
ma = F – Fтр; 3ma = 2F – Fтр
 3(F – Fтр)
= 2F – Fтр
3(F – Fтр)
= 2F – Fтр  Fтр = F/2.
Fтр = F/2.
С другой стороны, сила трения Fтр
= 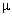 N =
N = 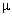 mg. С учётом этого
получим
mg. С учётом этого
получим 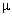 = 0,25.
= 0,25. 
3. Шарик массой m1 налетает на
другой, покоящийся. После упругого лобового
удара импульсы шариков стали одинаковыми.
Найдите массу m2 первоначально
покоившегося шарика.
Решение
Импульс тела р выражается через
его массу и скорость: p = m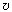 . Кинетическая энергия выражается
через импульс:
. Кинетическая энергия выражается
через импульс: 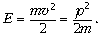
После упругого лобового удара
сохраняется полный импульс и полная
кинетическая энергия системы шариков, и они
движутся вдоль одной прямой (движение
одномерное). Пусть начальный импульс движущегося
шарика равен р0. Тогда, согласно закону
сохранения импульса и условию задачи, импульс
каждого шарика после удара равен р0/2.
С учётом этого запишем закон
сохранения кинетической энергии, выражая её
через импульс:
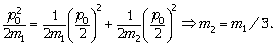
4. На проволочное кольцо радиусом R,
расположенное в вертикальной плоскости, надета
бусинка массой m. Бусинка соединена
пружинкой с центром кольца. Пружинка
деформирована так, что в состоянии покоя кольцо
действует на бусинку с силой, равной mg,
направленной вниз. Кольцо раскрутили вокруг
вертикальной оси так, что бусинка перестала
давить на кольцо. Определите угловую скорость
вращения кольца 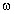 и угол
и угол 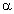 , на
который пружинка отклонилась от вертикали.
Трением пренебречь.
, на
который пружинка отклонилась от вертикали.
Трением пренебречь.
Решение
В состоянии покоя на бусинку действуют
сила упругости F, направленная
вверх, сила тяжести mg и сила
реакции со стороны кольца N, равная
силе тяжести, направленные вниз. Сумма этих сил
равна нулю:
F – mg – mg = 0  F = 2mg.
F = 2mg. 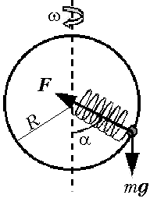
При вращении кольца бусинка движется
по окружности радиусом r = Rsin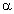 , где
, где 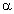 – угол между пружинкой и вертикалью. Так
как длина пружинки неизменна, величина силы
упругости F остаётся той же самой. Выписывая
второй закон Ньютона в проекциях на вертикаль и
горизонталь, в этом случае имеем:
– угол между пружинкой и вертикалью. Так
как длина пружинки неизменна, величина силы
упругости F остаётся той же самой. Выписывая
второй закон Ньютона в проекциях на вертикаль и
горизонталь, в этом случае имеем:
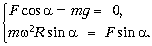
Совмещая все уравнения, находим 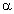 =
= 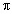 /3 = 60°,
/3 = 60°, 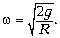
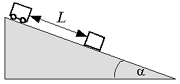
5. На шероховатой наклонной плоскости с
коэффициентом трения 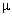 , образующей угол
, образующей угол 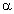 с горизонтом, покоится тело. Тележка,
которая вначале находилась на расстоянии L
от тела, начинает скатываться. На какое
максимальное расстояние сдвинется вниз тело,
если удары между ним и тележкой абсолютно
упругие? Массы тележки и тела одинаковы. Трением
тележки при её движении можно пренебречь.
с горизонтом, покоится тело. Тележка,
которая вначале находилась на расстоянии L
от тела, начинает скатываться. На какое
максимальное расстояние сдвинется вниз тело,
если удары между ним и тележкой абсолютно
упругие? Массы тележки и тела одинаковы. Трением
тележки при её движении можно пренебречь.
Решение
Обозначим искомое расстояние через х.
В конце концов тело и тележка будут покоиться,
контактируя между собой. Так как при ударах
потерь кинетической энергии (перехода её в
теплоту) нет, полный баланс энергии запишется в
виде: изменение кинетической энергии плюс
изменение потенциальной энергии равно работе
внешних сил (здесь – силы трения):
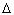 Eкин+
Eкин+
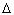 Uпот =
Aтр.
Uпот =
Aтр.
Начальная и конечная кинетические
энергии тела и тележки равны нулю, т.е. 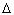 Eкин = 0.
Eкин = 0.
Потенциальная энергия тела
уменьшилась на mgхsin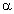 , а тележки – на mg(L + х)sin
, а тележки – на mg(L + х)sin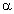 :
:
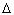 Uпот
= –mg(L + 2х)sin
Uпот
= –mg(L + 2х)sin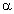 .
.
Сила трения, действующая на тело (на
тележку она не действует), равна Fтр = 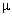 N =
N = 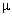 mgcos
mgcos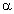 . Работа силы трения
. Работа силы трения
Aтр = –Fтрх =
–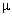 mgcos
mgcos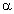 • х.
• х.
Объединяя уравнения, получим:
mg(L + 2х)sin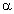 =
= 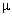 mgcos
mgcos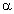 • х
• х  (L + 2х)sin
(L + 2х)sin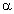 =
= 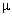 cos
cos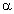 • х
• х 
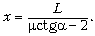
При 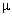
 2tg
2tg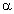 ответ не имеет смысла, т.к. в этом случае
тело с тележкой будут всё время соскальзывать.
ответ не имеет смысла, т.к. в этом случае
тело с тележкой будут всё время соскальзывать.
11-й КЛАСС
1. См. задачу 3 для 9-го класса.
2. См. задачу 4 для 10-го класса.
3. См. задачу 5 для 10-го класса. 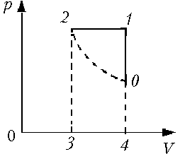
4. Два моля разреженного газа сначала
нагревают при постоянном объёме так, что
абсолютная температура газа возрастает в 2 раза,
а затем сжимают при постоянном давлении, доводя
температуру до первоначального значения T0
= 200 К. Какая работа была совершена при сжатии?
Универсальная газовая постоянная R = 8,31
Дж/(моль • К).
Решение
Пусть точка 0 соответствует
начальному состоянию. Согласно уравнению
состояния Менделеева–Клапейрона, pV = 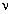 RT (в начальном
состоянии p0V0 =
RT (в начальном
состоянии p0V0 = 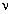 RT0). Процесс 0–1
– изохорный. По условию задачи, в этом процессе
давление возрастает в 2 раза, поэтому температура
возрастает тоже в 2 раза, т.е. p1 = 2p0;
T1 = 2T0.
RT0). Процесс 0–1
– изохорный. По условию задачи, в этом процессе
давление возрастает в 2 раза, поэтому температура
возрастает тоже в 2 раза, т.е. p1 = 2p0;
T1 = 2T0.
Так как в процессе 1–2 температура
возвращается к исходному значению при
постоянном давлении 2p0, то объём в
точке 2 станет V0/2 (уравнение
состояния имеет вид 2p0V0/2 = 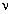 RT0).
RT0).
По определению, работа A в
процессе 1–2 равна площади прямоугольника 12341,
т.е.
A = 2p0 • 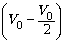 = p0V0 =
= p0V0 = 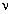 RT0;
RT0;
А = 2 • 8,31 • 200 = 3324 (Дж). 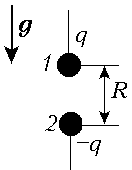
5. Два небольших одинаковых, сделанных
из материала плотностью 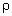 ш шарика заряжены одинаковыми по
величине, но противоположными по знаку зарядами q
и –q. Шарики подвешены на тонких длинных
нитях, проходящих через одну вертикаль, так что
расстояние между шариками равно R. После
того, как пространство заполнили керосином,
оказалось, что натяжение нити, к которой привязан
шарик 2, не изменилось. Найдите силу
натяжения этой нити и массу одного шарика.
Плотность керосина
ш шарика заряжены одинаковыми по
величине, но противоположными по знаку зарядами q
и –q. Шарики подвешены на тонких длинных
нитях, проходящих через одну вертикаль, так что
расстояние между шариками равно R. После
того, как пространство заполнили керосином,
оказалось, что натяжение нити, к которой привязан
шарик 2, не изменилось. Найдите силу
натяжения этой нити и массу одного шарика.
Плотность керосина 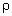 к, его диэлектрическая
проницаемость
к, его диэлектрическая
проницаемость 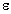 =
2.
=
2.
Решение
Проекция на вертикаль векторной суммы
сил, действующих на шарик 2 (сила натяжения
нити, сила тяжести и кулоновская сила), равна
нулю:
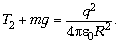
После заполнения пространства
керосином кулоновская сила уменьшается в 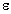 раз, но появляется
дополнительная сила Архимеда:
раз, но появляется
дополнительная сила Архимеда:
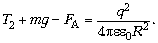
Решая совместно оба уравнения и
учитывая, что, по условию, 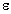 = 2, получим:
= 2, получим:
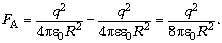
Пусть объём одного шарика V.
Учитывая, что FA = 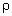 кVg, находим объём шарика:
кVg, находим объём шарика:
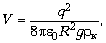
а затем массу шарика 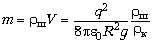 и силу натяжения нити:
и силу натяжения нити:
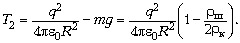
______________________
Запросы следует направлять директору
заочной школы СУНЦ НГУ Кутузовой Ольге
Ивановне (kutuzova@sscadm.nsu.ru)
или 630090, Новосибирск-90, ул. Ляпунова, 3, заочная
школа СУНЦ НГУ; тел. (3833) 39-7889.