Переписка с читателями Читатель А.Б.Рыбаков (гимназия № 144, г. Санкт-Петербург) сделал ряд критических замечаний по поводу некоторых публикаций в нашей газете. Отвечают авторы этих публикаций. Замечание 1. В «Физике» № 8/06 профессор (Менский М.Б. – Ред.) пишет о фотоэффекте и уравнении Эйнштейна. Я скромный школьный учитель, но, простите, здесь всё неправильно. Я своему ученику за такой ответ даже тройки бы не поставил. Электрон, выбитый квантом света из атома (поскольку речь идёт о металлах, правильнее было бы говорить об ионах) имел бы энергию h – E2i (E2i – энергия второй ионизации, т.е. выбивания электрона с какого-то уровня иона). В принципе описанный процесс (выбивание светом из металла атомных электронов), наверное, может иметь место (если энергия падающих квантов велика). Не знаю, наблюдаются ли эти процессы, мне таких данных видеть не приходилось. Но в любом случае уравнение Эйнштейна никакого отношения к таким процессам не имеет. В уравнении Эйнштейна стоит максимальная кинетическая энергия вылетевших из металла электронов (в рассуждениях М. вообще нет этого слова). А энергия будет максимальной у электронов, которые, поглотив квант, ничего не потратили ни на тепло, ни на выход из иона. То есть речь идёт о выбивании свободных электронов. И рисунок рядом только вводит в заблуждение. Кстати, вернулся Нильс Бор в Копенгаген не весной 1912 г., как пишет М., а осенью. И не весной 1913 г. «наступило неожиданное прозрение», а в первых числах февраля. И не «он наткнулся» на работу Бальмера, а «его натолкнули». Ну это я уже придираюсь... Ответ проф. М.Б.Менского (ФИРАН, г. Москва, mensky@mail.ru). Первое замечание читателя касается терминологии. Я называю энергию, потерянную электроном при выходе из металла и обозначенную у меня через A, работой выхода, не конкретизируя её природу. Это общепринятая терминология. Читатель указывает на одну из возможных причин потери энергии и по-другому обозначает её через E2i. Окончательная формула при этом оказывается той же самой, с учётом другого обозначения потерянной энергии. Что касается мелких деталей биографии Нильса Бора, то они взяты из воспоминаний современников. Читатель, видимо, читал другие источники, которые не обязательно являются более надёжными. Замечание 2. В том же номере опубликована статья «Диффузия или конвекция?» – Главную формулу, используемую автором для оценки времени распространения запаха, автор достаёт «из рукава». Не буду вникать в детали, скажу лишь, что во всех серьёзных источниках эта формула приводится как оценка времени выравнивания концентрации (например: Л.Д.Ландау и др. Курс общей физики. – М., 1969, с. 351). Согласитесь, что это нечто совсем другое. – «Расчёт» скорости конвекции на с. 17, конечно, никакого смысла не имеет. Нельзя вести расчёт, не прояснив модель. Почему можно «пренебречь изменением плотности»? Так можно получить любое число. Кстати, хорошо известно, что даже в начальный момент ускорение будет не таким, как думает автор, а уж при движении... один Бог знает. – Самодиффузия – это не какое-то «расплывание в пространстве» (в вакууме, что ли?), а расплывание молекул в среде себе подобных. Но какое отношение имеет самодиффузия к рассматриваемым процессам? – Почему автор думает, что 0,1•10–4 по порядку величины равно 10–4? – Почему молярная масса в рамках одной статьи обозначается по-разному? Ответ А.А.Князева (ЛПН, г. Саратов, knf@sgu.ru). Скажу сразу, что мне эта моя статья нравится. Пример с распространением духов в комнате не простой, говорят о нём довольно часто, чуть ли не от Перельмана. А у меня даже с оценками в определённой степени получилось, – долго не представлял себе, как сделать школьный вариант. Оценки, может быть, «дохленькие», но суть проблемы вполне отражают, а других не встречал. Отвечаю по пунктам. – По поводу «главной формулы» не соглашусь. Если нужен авторитет, то обратимся к Ландау: на с. 351, 3-й абзац: «…Каково среднее расстояние L, на которое успеет распространиться диффундирующее вещество за промежуток времени t?.. Очевидно, что ответ даётся той же формулой…» Кстати, благодарен читателю: впервые обратил внимание, что московские лекции Л.Д.Ландау 1937 г. называются «Курс общей физики». Имя Ландау прочно связано с курсом теоретической физики. Во-вторых, оказывается, на этой странице книги, собственно, и изложена первая часть обсуждаемой статьи – и про одну молекулу, и про ансамбль. Что поделаешь, преподавание вполне закономерно построено на компиляциях. – В статье практически нигде не предполагается «расчёт», а приводимая задача о конвекции уже довольно известна и, мне казалось, не требует прояснения. Собственно, статья посвящена приложению метода оценки к сложным явлениям со слабо определёнными данными. При разумных посылках в оценке получается вовсе не любое число (кстати, при чём здесь пренебрежение «изменением плотности»?). Тем не менее было бы куда лучше, если бы оппонент предложил свои результаты, полученные более строго и при этом опрокидывающие уже сделанные оценки. – Рассматриваемые процессы относятся к взаимодиффузии. Об этом в статье имеется соответствующее замечание. Для школы вряд ли всё это нужно усложнять, хотя у А.Р.Зильбермана в Соросовском комплекте есть хорошая задача о движении в ансамбле молекул разных сортов. – Оценка по порядку величины – это и есть разница в несколько раз, обычно в пределах десяти. Здесь можно было бы «поиграть» и уменьшить разницу. Я не стал, поскольку любой из этих результатов подтверждает тот факт, что диффузия – медленный процесс. Впрочем, формулировка, признаю, неудачная. – Молярная масса действительно обозначена по-разному (М и m) – это описка. Остаюсь благодарным читателю за отклик на публикацию. Мне думается, что распространение известного в науке метода оценки может внести в школу свежую струю. Пока, несмотря на усилия передовых педагогических школ, в преподавании явно доминируют две методики: в младших классах решение скучных задач по примитивным схемам, а в старших – пространные рассуждения о квантах и кварках. Уверен: что бы ни говорили нынешние реформаторы, обучение физике без решения задач ущербно. Другое дело, когда и какие задачи решать. Я за то, чтобы в классе рассматривались только хорошие задачи – их составляют олимпиадные композиторы. И тогда оценки способны расцветить «разговоры о физике», когда речь заходит об очень сложных, но ужасно интересных явлениях. Примеры использования этого метода уже проскакивают в учебниках. Вот, например, у В.А.Касьянова есть несколько симпатичных и достаточно свежих оценок. Иногда оценки вполне претендуют даже на определённую строгость (вспомните, например, задачу Седова о мощности ядерного взрыва, ведь строгое автомодельное решение практически совпадает с оценкой по размерности). А иногда вот вызывают раздражение. Присоединяйтесь, может быть, у вас получится лучше. Готов продолжить дискуссию в личной переписке. Замечание 3. К сожалению, не удалось понять самого главного в «Морских приливах» (№ 10/06, с. 40, левая колонка, начиная с 14-й строки снизу): «Поле отталкивающих сил однородно (чем дальше от оси вращения, тем центробежные силы больше. – Ред.) по интенсивности, его силовые линии параллельны». Господи, что здесь написано?! «Интенсивность» поля? Так однородно или увеличивается? Чувствую, что образования не хватает. Ответ проф. А.В.Некрасова (РГГМУ, г. Санкт-Петербург, nekrasov@rshu.ru ). Текст, действительно, получился непонятным – из-за не совсем корректного редакторского сокращения. 11 строк, начиная с конца 19-й строки снизу, следует заменить cледующим текстом: «Важно отметить, что это обращение происходит поступательно, т.е. без вращения Земли. Поэтому все точки Земли синхронно описывают круговые орбиты одинакового радиуса и, следовательно, испытывают действие одинаковых по величине и направлению центробежных сил. Таким образом, поле отталкивающих сил однородно как по интенсивности, так и по направлению, поскольку его силовые линии в каждый момент времени параллельны линии центров Луна–Земля. В то же время поле сил, притягивающих Землю к Луне, неоднородно, оно усиливается (обратно пропорционально квадрату расстояния)...» (далее по тексту). 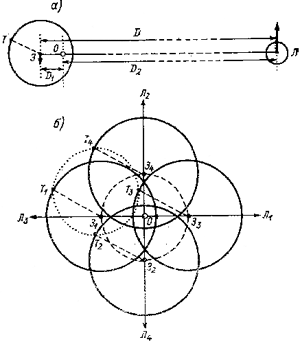Система Земля–Луна а) Обращение системы Земля–Луна вокруг её центра масс О (рисунок в плоскости вращения). Здесь З – центр Земли, D – расстояние между центрами Земли и Луны, D1 и D2 – расстояния между центром масс и соответственно центрами Земли и Луны (радиусы их орбитального движения), Т – произвольная точка на поверхности Земли. б) «Земная часть» орбитального движения. Показаны четыре последовательных положения Земли при её полном обороте вокруг центра масс О. Нижними цифровыми индексами для каждого из моментов помечены меняющееся направление на Луну (Л), а также положения центра Земли (З) и произвольной точки (Т). Очевидно, что каждая точка Земли (например, З и Т) совершает одинаковое круговое перемещение (точечная и прерывистая окружности). При таком движении любая прямая линия (например, линия ЗiТi) остаётся параллельной самой себе (признак поступательного движения). Лучше понять характер движения Земли вокруг общего центра масс системы Земля–Луна, возможно, поможет рисунок (см. слева) из моей книги «Энергия океанских приливов» (Л.: Гидрометеоиздат, 1990, с. 6, рис. 1.1), смысл которого я постарался здесь разъяснить максимально пространно. Замечание 4. Материалы К.Ю.Богданова (все!) и М.А.Бражникова в № 8 – замечательны. От редакции. Спасибо на добром слове. К вопросам читателя В.Н.Сотникова (г. Старый Оскол, Белгородская обл.) – см. «Физику» № 7, 15/06 – возвращается А.А.Князев (ЛПН, г. Саратов). – «Что измеряет вольтметр?» Вольтметр используют для измерения как разности потенциалов, так и напряжения (это никогда не одно и то же, см. ниже), и ЭДС. Значит, будучи индикатором этих величин, он не измеряет ни того, ни другого. Собственно, существует лишь один прибор – гальванометр, – стрелка которого отклоняется при прохождении через него тока. А шкалу можно сделать любую – для температуры, влажности и т.п. Главное, чтобы измеряемая величина была пропорциональна уже прошедшему току. И совершенно безразлично, чем вызван этот ток: разностью потенциалов (потенциальными силами), электромагнитной индукцией (сторонними вихревыми силами), химической ЭДС или даже механическим движением. Так что, если говорить в общем смысле именно о вольтметре, то он градуируется по падению напряжения на своем внутреннем сопротивлении, т.е. по работе диссипативных сил электрического сопротивления при проталкивании через него единицы заряда. 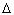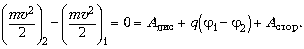Эта работа равна I2R t, как следует из теоремы о кинетической энергии носителей заряда в цепи на промежутке времени: Здесь слева – усреднённая разность кинетических энергий (она при постоянном токе равна нулю), справа – сумма работ действующих в цепи сил. Это, во-первых, упомянутые уже силы сопротивления; во-вторых, электростатические (потенциальные) и, наконец, остальные – сторонние. Иное дело электроскоп – в нём практически нет тока. При известном значении электроёмкости его показания (изменение угла между листочками) пропорциональны изменению потенциала листочков. Значит, может служить индикатором заряда. Когда-то на этом вопросе даже Эйнштейн с Инфельдом «попались», – все, наверное, знают эту историю. Знаю В.Н.Сотникова по публикации в журнале «Физика в школе» (№ 6, 2002). Это думающий специалист, просто недостаточно владеет литературой. – «Как показать, что при движении электрических зарядов появляются силы, отличные от кулоновских и напрямую зависящие от скорости движения этих зарядов? Это явление находится в полном соответствии со СТО». Электромагнитное взаимодействие описывается в современной теории шестикомпонентным электромагнитным полем. Этот факт до сих пор в явном виде практически не сформулирован в учебной литературе. Имеет смысл рассмотреть различные ситуации проявления электрического и магнитного полей. Например, в такой последовательности: неподвижная группа зарядов, равномерное движение, постоянный ток в проводниках, постоянный магнит, ускоренное движение, распространяющееся излучение. Тогда снимутся все вопросы о соотношении значений магнитной и электрической компоненты силы, и о роли релятивизма.

.  .