Рекомендации по изложению СТО с учётом требований СтандартаИзложение темы «Элементы СТО», как
правило, базируется на наиболее
распространённом учебнике для базовой школы Г.Я.Мякишева
и Б.Б.Буховцева (М.: Просвещение, 1993–2006 гг.,
§ 75–80, по изд. 2004 г.), изложение релятивистской
динамики в котором основано на устаревшем
понятии массы, зависящей от скорости (m
= E/c2). Соответственно вводится
термин «масса покоя» m0 при скорости
тела Вторым некорректно изложенным вопросом является сокращение длины (как следствие постулатов СТО). Мы считаем необходимым указать на эти недостатки с тем, чтобы учитель мог скорректировать изложение теории относительности. О сокращении длины. Ошибка (точнее, недоговорённость), допущенная в учебнике Г.Я.Мякишева и Б.Б.Буховцева (а также в учебнике С.В.Громова под ред Н.В.Шароновой и, возможно, в другой учебной литературе) состоит в том, что в нём ни слова не говорится о необходимости проводить измерения концов движущегося тела (стержня) в один и тот же момент времени по часам в движущейся системе K, чтобы затем сравнить его длину L в системе K с его же длиной L0 в системе K', где он покоится. Этот явный недосмотр тянется уже десятилетиями. В результате появляются абсурдные задачи типа: «С какой скоростью должен двигаться космический корабль, чтобы пройденный им путь при измерении с Земли оказался вдвое короче?» Изменяются только длины масштабов (в предположении правильной процедуры измерения!), а никак не расстояния. Вопрос об изменении длины движущегося
тела – непростой. Известно, что сам А.Эйнштейн
считал, что движущийся с релятивистской
скоростью шар неподвижному наблюдателю будет
казаться эллипсоидом. И только через 50 лет после
его смерти было показано, что шар всегда и всем
будет казаться шаром. Однако в рамках школьной
программы показать это невозможно. Единственно
правильным, на наш взгляд, решением в такой
ситуации является отказ от изложения этого
вопроса и от всех связанных с ним задач. Кстати, в
солидном учебнике для школ с углублённым
изучением физики под ред. А.А.Пинского вопрос о
сокращении длины даже не упоминается. Надо
заметить, что нам неизвестно ни одно прямое
приложение формулы О формуле Е = mc2. Намного важнее замечания, касающиеся понятия массы и энергии в СТО. Предварительно заметим, что ни в одном учебном пособии для школы невозможно логически безупречно изложить этот вопрос. В какой-то момент приходится постулировать то или иное соотношение без объяснений. Причина ясна: безупречный путь построения СТО от постулатов к окончательным формулам требует использования физических понятий и математического аппарата, существенно выходящих за рамки доступного для школьников и, кроме того, не может быть изложен за 6 ч, а тем более за 2 ч. Доступное для учителей школ любого уровня изложение основ СТО содержится в превосходной книге В.А.Угарова «Специальная теория относительности» (М.: Физматгиз, 1977). Сейчас понятие массы, зависящей от скорости, изъято из школьной программы. Следовательно, необходимо перейти к новой схеме изложения основ СТО, например, к представленной ниже, позволяющей корректно объяснить вопрос о взаимосвязи массы и энергии. После формулировки постулатов СТО мы рекомендуем сделать следующие шаги: 1. Постулировать преобразования Лоренца для координат события:
Здесь x0 = ct, 2. Ввести понятие четырёхмерного вектора (4-вектора) координат точки в четырёхмерном пространстве событий с координатами (x0, x, y, z). Доказать (на основе преобразований Лоренца), что интервал (или квадрат 4-вектора), равный s2 = c2t2 – x2 – y2 – z2 = (x0)2 – r2, является инвариантом лоренцовских преобразований, т.е. одинаков во всех ИСО. 3. Постулировать, что 4-вектором называется совокупность четырёх чисел, преобразующихся при переходе из одной ИСО в другую так же, как координаты события. Провести аналогию с обычным вектором в трёхмерном пространстве. 4. Постулировать 4-вектор энергии-импульса элементарной частицы массой m и компонентами р (E/c, px, py, pz). Для компонент этого 4-вектора выписать преобразования Лоренца от системы K в систему K', в которой частица покоится:
Квадрат вектора равен p2 = E2/c2 – p2 = m2c2. Соотношение Эйнштейна E2/c2 – p2 = m2c2 (2) является основным соотношением теории. Оно постулируется, и это ничем не хуже, чем постулирование формулы (9.6) в указанном выше учебнике Г.Я.Мякишева и Б.Б.Буховцева. 5. Объяснить, что масса m – характеристика элементарной частицы, определённая природой и являющаяся инвариантом лоренцовских преобразований (т.е. эта масса одинакова во всех ИСО). Если элементарная частица покоится, то её энергия покоя Е0 = mc2. Именно эту формулу следует цитировать, обыгрывать и включать в стихи и песни. Если масса элементарной частицы равна нулю (фотон), то величина импульса такой частицы |p| = E/c – это следует из формулы (2). 6. С помощью преобразований Лоренца для четырёхмерного вектора энергии–импульса легко устанавливается еще одно соотношение: p = E 7. Важнейший этап – проверка
формул (2) и (3) в пределе малых скоростей
(нерелятивистское приближение). Тогда, с
точностью до квадратичных слагаемых по
отношению к ( Е = mc2 + p2/2m;
р = m 8. Из формулы (1) следует связь
между Е и Е' (в штрихованной системе
импульс частицы равен нулю, т.к. частица
покоится): E =
Из формул (3) и (5) вытекает:
9. При рассмотрении основных формул динамики отдельной элементарной частицы никаких других масс, кроме массы частицы (её даже не надо называть массой покоя, это автоматически подразумевается), вводить не нужно. Энергия покоя элементарной частицы, согласно соотношению Эйнштейна, равна произведению массы частицы на квадрат скорости света. 10. Следующий по сложности случай – система, состоящая из невзаимодействующих элементарных частиц, обладающих каждая определённой скоростью и, следовательно, кинетической энергией Tкин. В этом случае полная энергия системы равна сумме энергий покоя всех частиц плюс сумма их кинетических энергий:
Если ввести величину М = Е/c2 и назвать её массой системы, то можно записать:
При рассмотрении системы частиц удобно пользоваться понятием «масса M системы». Из (7) вытекает, что М > m, т.к. кинетическая энергия частиц всегда положительна. 11. Наиболее интересен случай системы, состоящей из взаимодействующих частиц. Обозначим энергию взаимодействия U. Тогда
Для системы в равновесии U < 0. Например, это относится к гравитационной энергии связи планеты или звезды, для энергии связи нуклонов в ядре. В системе отсчёта, где суммарный импульс всех частиц равен нулю (система центра инерции):
Иными словами, сложная система, состоящая из взаимодействующих элементарных частиц (или частиц, которые можно на данном уровне рассмотрения считать элементарными), обладает массой системы, которая не равна сумме масс отдельных невзаимодействующих частиц, а меньше суммы этих масс на величину, называемую дефектом масс:
По дефекту масс можно вычислить энергию связи
В любом устойчивом теле M = А.В.БЕРКОВ, к.ф.-м.н.,
|
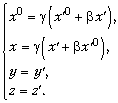
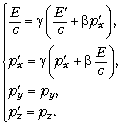 (1)
(1)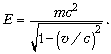 (5)
(5)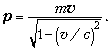 (6)
(6)