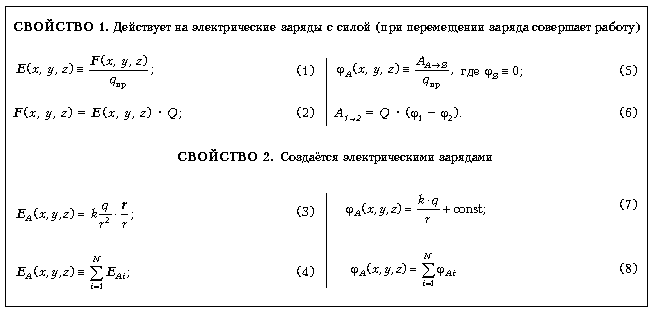ПРИЁМЫ И НАХОДКИ А.В.КОНДРАТЬЕВ, школа № 1189 им. И.В.Курчатова, г. Москва ollandr@yandex.ru Электростатическое поле Два подхода к описанию. 10-й класс У русских профессоров старой школы существовала традиция делать вводные обзоры к своим предметам. Беглый взгляд на материал в целом, изложение всех основных идей в начале курса стимулирует у слушателей интерес к деталям – возникает желание «приблизить картинку». Универсальность подхода к описанию электростатического поля в терминах напряжённости и потенциала заслуживает того, чтобы сказать о нём не только при повторении, но и в самом начале изучения электростатики. Электростатическое поле не имеет цвета и запаха, его нельзя увидеть или потрогать руками. Все знания о нём базируются на двух его свойствах. Первое: на электрический заряд, помещённый в электростатическое поле, действует сила, пропорциональная величине заряда. Второе: электрический заряд сам создаёт электростатическое поле, которое действует на другие заряды (своего поля заряд не ощущает). Оба свойства допускают количественное описание, причём двумя (почти) эквивалентными способами. Вид доски в конце урока: описание электростатического поля с помощью вектора напряжённости (слева) и потенциала (справа) – формулы записываются по ход Идея «силового описания» электростатического поля состоит в том, чтобы, взяв пробный заряд qпр, «ходить» с ним по всему пространству и измерять вектор силы F, действующей на qпр в каждой точке. Поскольку отношение F/qпр не зависит от величины пробного заряда (для другого пробного заряда отношение останется тем же), оно принимается в качестве векторной «силовой» характеристики поля – напряжённости E (формула 1). Если поле E всюду известно, на заряд Q, помещённый в точку, определяемую радиус-вектором r, действует сила, равная произведению заряда на вектор напряжённости (2). Таким образом, знание напряжённости поля позволяет предсказать, с какой силой поле подействует на заряд. Ходить по всему пространству с пробным зарядом и динамометром необязательно, т.к. есть относительно простые способы вычисления напряжённости E. Электростатическое поле создаётся неподвижными зарядами. Точечный заряд q создаёт вокруг себя поле, напряжённость которого по модулю спадает обратно пропорционально квадрату расстояния до этого заряда (формула 3). Любое заряженное тело (или несколько тел) произвольной формы можно мысленно разбить на точечные заряды. Принцип суперпозиции (формула 4) позволяет в любой точке пространства вычислить поле E как векторную сумму полей, создаваемых этими точечными зарядами. При «силовом описании» первое свойство электростатического поля позволяет дать определение напряжённости поля и формулу для вычисления силы, действующей на заряд в известном поле (мы различаем эти формулы). Второе свойство описывается формулами для поля, создаваемого точечным зарядом, и для принципа суперпозиции. Свойство поля «действовать на заряд с силой» относится к точке, т.е. является локальным свойством. Напряжённость поля является в этом смысле величиной локальной. Несмотря на прозрачный физический смысл вектора E, для практических целей более удобной оказывается другая возможность описания электростатического поля. Поскольку в каждой точке поля на заряд действует сила, при перемещении заряда эта сила совершает работу. Любое электростатическое поле устроено таким образом, что оно при перемещении заряда вдоль произвольной замкнутой кривой С на части пути «подталкивает» заряд, а на части «тормозит», и суммарная работа поля всегда оказывается равной нулю. Никакой деформацией кривой С невозможно добиться, чтобы электростатическое поле совершило ненулевую работу к моменту, когда заряд возвращается в исходную точку. В полях, обладающих таким свойством (они называются потенциальными), работа между двумя точками не зависит от пути следования (это легко доказать, рассматривая замкнутые пути, проходящие через любые точки 1 и 2, зафиксировав, например, прямой путь 1 2 и варьируя обратные 2 1). Переформулируем свойство электростатического поля – «действует на заряд с силой» – в его «нелокальный эквивалент» – «при перемещении заряда поле совершает работу». Идея «потенциального» описания: указать работу AAB, которую поле совершает при перемещении пробного заряда qпр из любой точки A в какую-нибудь заранее выбранную точку В. Отношение AAB/qпр определяется только полем (не зависит от величины qпр) и принимается в качестве энергетической характеристики поля в точке A – потенциала A (формула 5). Если потенциал везде определён, работа поля A12 при перемещении заряда Q между любыми двумя точками 1 и 2 определяется произведением заряда на разность потенциалов в этих точках (формула 6). (Смещение точки B, в которую мы вносим пробный заряд, изменяет потенциал во всех остальных точках на одну и ту же величину, поэтому для вычисления работы поля, зависящей от разности потенциалов, выбор точки B совершенно несуществен.) Знание потенциала в любой точке позволяет предсказать, какая работа будет совершена полем при произвольном перемещении заряда. Популярность описания поля с помощью потенциала связана с тем, что информация о работе поля зачастую оказывается гораздо более полезной, чем информация о силе, действующей на заряд. Конечно, зная напряжённость поля, можно работу вычислить, но математическая проблема, которая при этом возникает (криволинейный интеграл от векторной функции), оказывается обычно сложнее использования формулы A12 = Q • (1 – 2). Потенциал в любой точке можно рассчитать по заданному распределению создающих поле зарядов. Для этого, во-первых, необходимо знать формулу для потенциала на расстоянии r от точечного заряда (7). (Значение константы зависит от того, в какой точке потенциал принимается за нулевой. Физики точку нулевого потенциала обычно выбирают на бесконечности, и постоянная в этой формуле исчезает. Электротехники нулевой потенциал приписывают проводникам очень большой ёмкости и говорят, что «земля имеет нулевой потенциал».) Во-вторых, нужен принцип суперпозиции (формула 8), позволяющий вычислить потенциал, если поле создаётся системой зарядов. Здесь уже складываются числа, а не векторы. Таким образом, на два свойства электрического поля (дающих рецепт его обнаружения и создания) приходится по четыре формулы – на каждый способ описания. Напряжённость и потенциал содержат почти одинаковое количество информации о поле. По заданному распределению потенциала в пространстве напряжённость поля находится однозначно. Обратное верно при условии, что указана точка, где потенциал принимается равным нулю. Литература Куринский В.А. Автодидактика. – М.: Автодидакт, 1994. Шилейко А.В., Шилейко Т.И. В океане энергии. – М.: Знание, 1989. Андрей Владимирович Кондратьев закончил физфак МГУ им. М.В.Ломоносова в 1997 г. по специальности «Физика». С 1995 г. – учитель физики в школе № 1189. Считает, что газета «Физика» очень важна, ведь своя профессиональная газета – это зачастую единственная поддержка, а иногда и соломинка для тех, кто работает в несчастной российской школе. Это именно то, что нужно, особенно начинающим.

.  .