ИНТЕРАКТИВНЫЕ
ТЕХНОЛОГИИ
Е.М.РАВОДИН,
МОУ СОШ № 2, г. Прокопьевск
ravodin@bk.ru
Изучение колебательного контура
Эксперимент с использованием
компьютера. 10-й класс
Для иллюстрации объяснения работы
колебательного контура и анализа происходящих в
нём процессов рекомендую использовать свою
авторскую программу «Kontur», выложенную на
сайте http://ssmu.ru/er/ и доступную
для всех.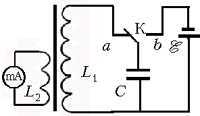
Оборудование: колебательный
контур, состоящий из дроссельной катушки L1
(3600 витков), надетой на замкнутый сердечник
универсального трансформатора, и конденсатора C
ёмкостью 500 мкФ; демонстрационный амперметр,
подключённый как гальванометр к обмотке второй
дроссельной катушки L2 (25 витков);
источник постоянного напряжения (около 30 В,
например, ИЭПП1); переключатель. Схема установки
приведена на рисунке.
Ход урока
1. Актуализация знаний
Фронтальная беседа
– В чём состоит закон сохранения
энергии? (Ответ. В замкнутой системе полная
энергия не изменяется.)
– Как рассчитать энергию магнитного
поля катушки? (Ответ. Eм = LI2/2.)
– Как рассчитать энергию
электрического поля конденсатора? (Ответ. Еэ
= CU2/2; Eэ= q2/(2C).)
– В чём заключается явление
самоиндукции и как рассчитывают величину ЭДС
самоиндукции и её направление? (Ответ.
Явление самоиндукции есть возникновение ЭДС
индукции 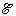 si
в проводнике, в котором изменяется сила тока;
si
в проводнике, в котором изменяется сила тока; 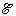 si
направлена так, чтобы противодействовать
изменению силы тока и рассчитывается по формуле
si
направлена так, чтобы противодействовать
изменению силы тока и рассчитывается по формуле 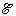 si = –LI't,
где I't – производная силы тока по времени.)
si = –LI't,
где I't – производная силы тока по времени.)
– Какие колебания являются
гармоническими? (Ответ. Это колебания, при
которых колеблющаяся величина зависит от
времени по закону синуса или косинуса, а её
вторая производная пропорциональна этой
величине и имеет противоположный знак (x"t
= –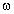 2x),
причём коэффициентом пропорциональности
является квадрат циклической частоты.)
2x),
причём коэффициентом пропорциональности
является квадрат циклической частоты.)
– Что такое сила тока? (Ответ. Это
производная от заряда по времени: I = q'.)
2. Объяснение нового материала
Учитель объясняет, что система из
замкнутых друг на друга катушки и конденсатора
называется колебательным контуром, показывает
собранную установку, демонстрирует и объясняет
её схему (см. рисунок). Катушка L1 и
конденсатор С образуют колебательный контур.
Если нож переключателя К перебросить в положение
b, то конденсатор зарядится до напряжения U
= 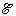 (где
(где 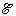 – ЭДС источника тока) и
получит энергию Eэ = q2/(2C).
Демонстрирует, что при перебрасывании
переключателя в положение а при заряженном
конденсаторе миллиамперметр регистрирует
затухающие колебания. Далее учитель поясняет
суть происходящих процессов с применением
программы «Kontur». (Перед уроком
рекомендуется, ознакомившись с программой,
запустить её и выбрать удобный вариант и темп
исполнения.)
– ЭДС источника тока) и
получит энергию Eэ = q2/(2C).
Демонстрирует, что при перебрасывании
переключателя в положение а при заряженном
конденсаторе миллиамперметр регистрирует
затухающие колебания. Далее учитель поясняет
суть происходящих процессов с применением
программы «Kontur». (Перед уроком
рекомендуется, ознакомившись с программой,
запустить её и выбрать удобный вариант и темп
исполнения.)
Рассмотрим, как использовать вариант,
запускаемый клавишей «р». На экране
появляется схема колебательного контура с
заряженным конденсатором, причём нижняя его
обкладка имеет положительный заряд, а верхняя –
отрицательный. Такое состояние контура в
дальнейшем будем считать начальной фазой (0). Вся
энергия контура локализирована в конденсаторе: Eэ
= qm2/(2C), где qm –
начальный, максимальный, заряд конденсатора.
Слева от контура схематически изображён
математический маятник в положении,
соответствующем той же фазе – он тоже обладает
потенциальной энергией Eп = kxm2/2,
где xm – начальное максимальное
смещение. Конденсатор начинает разряжаться
через катушку (в ней появляются ток I и
энергия Eм = LI2/2), а маятник
соответственно движется к положению равновесия,
увеличивая свою скорость и кинетическую энергию Eк
= m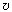 2/2.
Обращаем внимание учащихся на аналогии
механических и электромагнитных колебательных
процессов. Маятник из-за инертности постепенно
набирает скорость; ток, нарастающий в катушке,
вызывает изменяющееся магнитное поле (на экране
это изображается увеличением числа силовых
линий в катушке), что приводит к появлению ЭДС
самоиндукции
2/2.
Обращаем внимание учащихся на аналогии
механических и электромагнитных колебательных
процессов. Маятник из-за инертности постепенно
набирает скорость; ток, нарастающий в катушке,
вызывает изменяющееся магнитное поле (на экране
это изображается увеличением числа силовых
линий в катушке), что приводит к появлению ЭДС
самоиндукции 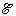 si,
не позволяющей току быстро нарастать. В
нижней части экрана можно видеть графики
изменения заряда q конденсатора и силы тока I
в катушке.
si,
не позволяющей току быстро нарастать. В
нижней части экрана можно видеть графики
изменения заряда q конденсатора и силы тока I
в катушке.
Заряд конденсатора начинает
уменьшаться (то же происходит и с его
потенциальной энергией), и это изображается
сокращением количества знаков «+» и «–» на
обкладках и уменьшением величины
соответствующих символов справа от
конденсатора. Слева от контура видно, что такой
же процесс превращения потенциальной энергии в
энергию, связанную с движением, происходит с
математическим маятником, который начал
колебания из фазы 0, соответствующей
максимальному отклонению от положения
равновесия и наибольшей потенциальной энергии.
Появившиеся на проводах и быстро растущие
красные стрелки обозначают нарастание силы тока
в контуре и, следовательно, увеличение энергии
магнитного поля, силовые линии которого
представлены зелёным цветом. Внизу
вычерчиваются графики заряда и тока, из которых
следует, что колебания этих величин происходят
со сдвигом фаз в четверть периода.
В любой момент учитель имеет
возможность остановить процессы, происходящие
на экране, нажав клавишу «пробел», дать
соответствующие разъяснения и продолжить работу
программы, нажав любую клавишу. Так, например,
задержав картинку в момент полной разрядки
конденсатора, педагог обращает внимание
учащихся на то, что этот момент соответствует
наибольшему току Im, наибольшей
энергии магнитного поля Eмmax = LIm2/2
(всё это наглядно отображается на мониторе). Так
же, как маятник, проходящий положение равновесия
в этой же фазе (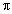 /2) и имеющий максимальную
скорость, не может мгновенно остановиться и
продолжает движение по инерции, так и ток контура
вследствие «электрической инерции» –
самоиндукции – не в состоянии мгновенно
прекратиться и продолжает течь в том же
направлении, заряжая снова конденсатор, но уже
при противоположной полярности. Нажав любую
клавишу, видим продолжение всех этих явлений.
Перезарядка конденсатора продолжается до тех
пор, пока не иссякнет энергия магнитного поля Eм
= LI2/2 в катушке, а замедленное движение
маятника – пока не обратится в ноль его
кинетическая энергия. Теперь в фазе
/2) и имеющий максимальную
скорость, не может мгновенно остановиться и
продолжает движение по инерции, так и ток контура
вследствие «электрической инерции» –
самоиндукции – не в состоянии мгновенно
прекратиться и продолжает течь в том же
направлении, заряжая снова конденсатор, но уже
при противоположной полярности. Нажав любую
клавишу, видим продолжение всех этих явлений.
Перезарядка конденсатора продолжается до тех
пор, пока не иссякнет энергия магнитного поля Eм
= LI2/2 в катушке, а замедленное движение
маятника – пока не обратится в ноль его
кинетическая энергия. Теперь в фазе 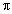 обе
колебательные системы (и контур, и маятник)
оказались в состоянии, похожем на исходное, но
противоположном по знаку заряда (для контура) или
по смещению (для маятника). Это же показывает и
график.
обе
колебательные системы (и контур, и маятник)
оказались в состоянии, похожем на исходное, но
противоположном по знаку заряда (для контура) или
по смещению (для маятника). Это же показывает и
график.
Далее объяснение аналогично от фазы 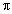 до 2
до 2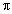 ;
рассказ учителя перемежается демонстрацией
статических и динамических картинок. После
завершения первого периода колебаний следуют
ещё два. При желании зафиксировать окончательную
картинку следует в конце третьего периода нажать
«пробел». В противном случае происходит выход из
программы.
;
рассказ учителя перемежается демонстрацией
статических и динамических картинок. После
завершения первого периода колебаний следуют
ещё два. При желании зафиксировать окончательную
картинку следует в конце третьего периода нажать
«пробел». В противном случае происходит выход из
программы.
Заметим, что переход от одного режима к
другому (например, показ только контура,
исключение графика или маятника) возможен и в
процессе её выполнения. Для возвращения на
начало (в меню) используют клавишу «s», для
выхода из программы – клавишу «Esc».
Если активное сопротивление контура
пренебрежимо мало, то энергия электрического
поля конденсатора полностью переходит в энергию
магнитного поля катушки; так же, без потерь,
происходят обратные переходы. Следовательно,
полная энергия в контуре остаётся неизменной:
q2/(2C) + LI2/2 =
сonst.
Взяв производную от этого выражения,
получим
2qq'/(2C) + 2LII'/2 = 0.
После упрощения получаем
qq'/C + LII' = 0.
Учитывая, что I = q', видим, что
q/C + Lq" = 0, или 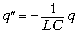 ,
,
т.е. вторая производная от заряда
пропорциональна заряду и имеет с ним
противоположный знак. А это значит, что в контуре
происходят гармонические колебания, причём 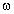 2 = 1/(LC)
– циклическая частота
2 = 1/(LC)
– циклическая частота 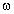 называется собственной, а значит,
период
называется собственной, а значит,
период
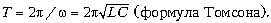
Замечаем, что, согласно формуле, с
уменьшением индуктивности L уменьшается и
период Т. Иллюстрируем закономерность на
установке: сдвигая сердечник в катушке (т.е.
уменьшая её индуктивность), наблюдаем уменьшение
периода колебаний. Если подключить
дополнительный конденсатор параллельно
основному (увеличиваем ёмкость), то наблюдаем
увеличение периода.
3. Закрепление материала
Решаем задачи № 980, 981 из сб. А.П.Рымкевича
и задачу № 5 из учебника В.А.Касьянова.
4. ДЗ. Задачи № 978, 979 из сб. А.П.Рымкевича.
Литература
Рымкевич А.П. Сборник задач по
физике для 8–10 классов средней школы. – М.:
Просвещение, 1988.
Касьянов В.А. Физика-11. – М.: Дрофа,
2002.

Евгений Михайлович Раводин – выпускник
Новокузнецкого ГПИ, заслуженный учитель школы
РФ, отличник народного просвещения,
педагогический стаж 48 лет, награждён орденами
«Знак Почёта» и Октябрьской Революции, медалью
«Ветеран труда», автор ряда компьютерных учебных
программ.