В.В.АЛЬМИНДЕРОВ, Л.К.БЕЛОПУХОВ,
А.И.ЧЕРНОУЦАН,
|
| Международный интеллект-клуб «Глюон» приглашает региональные центры, школы, лицеи и гимназии, работающие с одарёнными детьми, к участию в международных олимпиадах «Интеллектуальный марафон», которые проходят ежегодно в октябре. Заявки на участие присылайте по адресу: 115522, Москва, Пролетарский пр., 15/6, корп. 2, МИК «Глюон». Тел. (095) 517-8014, факс (095) 396-8227; e-mail: gluon@yandex.ru (см.также сайт: www.informika.ru/text/goscom/gluon). |
 Международный интеллект-клуб «Глюон» в
рамках международной программы «Дети. Интеллект.
Творчество» при участии университета
г. Ретимно (Греция), МГУ имени М.В.Ломоносова,
фонда некоммерческих программ «Династия» и при
поддержке компаний «Кирилл и Мефодий»,
«Физикон», «1С», ИД «Первое сентября» и журнала
«Квант» в октябре 2005 г. провёл очередную, XIV
международную тест-рейтинговую олимпиаду
«Интеллектуальный марафон-2005» на берегу
Средиземного моря в г. Ретимно (о. Крит). Одарённые
школьники из разных регионов России, Казахстана
и Норвегии соревновались в командных и
индивидуальных турах по математике, физике,
истории научных идей и открытий.
Международный интеллект-клуб «Глюон» в
рамках международной программы «Дети. Интеллект.
Творчество» при участии университета
г. Ретимно (Греция), МГУ имени М.В.Ломоносова,
фонда некоммерческих программ «Династия» и при
поддержке компаний «Кирилл и Мефодий»,
«Физикон», «1С», ИД «Первое сентября» и журнала
«Квант» в октябре 2005 г. провёл очередную, XIV
международную тест-рейтинговую олимпиаду
«Интеллектуальный марафон-2005» на берегу
Средиземного моря в г. Ретимно (о. Крит). Одарённые
школьники из разных регионов России, Казахстана
и Норвегии соревновались в командных и
индивидуальных турах по математике, физике,
истории научных идей и открытий.
Церемония открытия проходила в мэрии г. Ретимно, где выступили губернатор о. Крит, организаторы олимпиады, представители мэрии и участники олимпиады. Участники осмотрели достопримечательности здания мэрии, посетили знаменитый Кносский дворец и историко-археологический музей столицы острова г. Ираклиона. День завершился устными командными соревнованиями по истории научных идей и открытий в области физики-математики, экологии-биологии, истории и культурологии. Затем последовали напряжённые рабочие дни: каждый школьник участвовал в командных и индивидуальных соревнованиях. В один из экскурсионных дней участники познакомились со средневековым венецианским городом-крепостью Сфендони и осмотрели сталактит-сталагмитовую пещеру.
На церемонии закрытия организаторы и члены жюри поблагодарили участников за интересную совместную работу, а также всех, кто помогал в организации и проведении мероприятия. Особо было отмечено участие фонда «Династия» и компании «Кирилл и Мефодий». Во второй раз МИК «Глюон» совместно с ИД «Первое сентября» вручил специальный приз имени И.Л.Соловейчик лучшему ученику по математике и его учителю-математику. Церемония награждения прошла в праздничной обстановке. Всем участникам вручили сертификаты и памятные подарки олимпиады, а лучшие в индивидуальных и командных зачётах по всем номинациям были награждены дипломами, медалями, кубками и памятными сувенирами.
Абсолютным победителем олимпиады в командном зачёте стала сборная команда Краснодарского края. Ей был вручён главный приз соревнований – суперкубок и призы от спонсоров. Команда была также лучшей в турах по математике, истории научных идей и открытий и получила малые кубки этих соревнований. Второе место в общем зачёте заняла команда Классического лицея № 1 при РГУ (г. Ростов-на-Дону). Она также заняла первое место в туре по математике, второе место по физике и по истории научных идей и открытий. Команде были вручены большой кубок и дипломы за успехи в соответствующих командных соревнованиях. Общее третье место и третье место в туре по физике заняла сборная команда Татарстана (кубок и дипломы).
В биолого-экологическом направлении олимпиады победу одержала сборная Казахстана, на втором месте оказалась сборная Норвегии, на третьем – сборная России. Всем им были вручены кубки, дипломы и призы олимпиады.
В индивидуальных соревнованиях абсолютным победителем олимпиады стал Хапланов Арсений (11-й класс, Классический лицей № 1 при РГУ, г. Ростов-на-Дону): большая золотая медаль и малая золотая медаль за 1-е место по математике. Вторым призёром в общем зачёте стал Хохуля Никита (11-й класс, лицей ИСТЭК, г. Краснодар): большая серебряная медаль и малая серебряная медаль за 2-е место по физике. Большую бронзовую медаль в общем зачёте завоевал Омарбеков Алибек, представлявший центр «Дарын» (Казахстан).
В индивидуальном зачёте по физике лучшим стал Гарифулин Эльдар (11-й класс, Классический лицей № 1 при РГУ): малая золотая медаль. 2-е место по физике (см. выше) занял Хохуля Никита. Сошенко Владимир (10-й класс, МТЛ, г. Новороссийск) получил бронзовую медаль за 3-е место по физике.
Ниже приводятся задачи олимпиады.
ФИЗИКА
Письменный индивидуальный тур 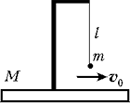
1. Брусок массой M стоит на гладкой горизонтальной плоскости. На бруске закреплён штатив, к которому на нити длиной l подвешен груз массой m. Какую наименьшую горизонтальную скорость надо сообщить грузу, чтобы он совершил полный оборот в вертикальной плоскости?
Решение. Запишем законы сохранения энергии и импульса для бруска с грузом:
![]()
где ![]() 1,
1,
![]() 2 –
скорости груза и бруска соответственно в момент
времени, когда груз находится в верхней точке.
Если груз проходит полный оборот вокруг точки
подвеса, то нить натянута во всех точках
траектории. При минимальной начальной скорости
натяжение в верхней точке обращается в ноль.
Второй закон Ньютона в этой точке запишем в
системе отсчёта, связанной с бруском:
2 –
скорости груза и бруска соответственно в момент
времени, когда груз находится в верхней точке.
Если груз проходит полный оборот вокруг точки
подвеса, то нить натянута во всех точках
траектории. При минимальной начальной скорости
натяжение в верхней точке обращается в ноль.
Второй закон Ньютона в этой точке запишем в
системе отсчёта, связанной с бруском: ![]() т.к. именно в этой системе
отсчёта радиус кривизны траектории груза равен
длине нити l. В системе отсчёта, связанной с
Землёй, точка подвеса нити перемещается вместе с
бруском, и груз движется по сложной траектории.
Отметим, что в рассматриваемый момент времени
ускорение бруска относительно Земли равно нулю,
т.е. связанная с ним система отсчёта является
инерциальной (сила инерции обращается в нуль).
т.к. именно в этой системе
отсчёта радиус кривизны траектории груза равен
длине нити l. В системе отсчёта, связанной с
Землёй, точка подвеса нити перемещается вместе с
бруском, и груз движется по сложной траектории.
Отметим, что в рассматриваемый момент времени
ускорение бруска относительно Земли равно нулю,
т.е. связанная с ним система отсчёта является
инерциальной (сила инерции обращается в нуль).
Выполнив преобразования (выразив ![]() 1 и
1 и ![]() 2 из второго и третьего
уравнений и подставив их в первое), получим:
2 из второго и третьего
уравнений и подставив их в первое), получим:
![]()
Замечание. Если вы знакомы с
важным свойством системы центра масс двух
материальных точек, гласящим, что кинетическая
энергия системы в этой системе отсчёта
выражается через относительную скорость точек: 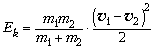 (это утверждение
несложно проверить «в лоб»), то можно решать эту
задачу в системе центра масс:
(это утверждение
несложно проверить «в лоб»), то можно решать эту
задачу в системе центра масс:
![]()
2. По одной из гипотез, звёзды
образуются из межзвёздной среды (космической
пыли) в результате сжатия под действием
гравитационных сил. Оцените время образования
звезды из гигантского сферического облака
космической пыли плотностью ![]() = 2 • 10–20 г/см3.
= 2 • 10–20 г/см3.
Решение. Так как все точки облака
движутся к центру, не опережая друг друга, то
частица, находившаяся изначально на расстоянии r
от центра, всё время притягивается к массе ![]() Найдём время
падения частицы на центр (конечное расстояние до
центра пренебрежимо мало по сравнению с
начальным, т.к. плотность возрастает на много
порядков). Заменим движение по прямой движением
по очень узкому эллипсу с большой осью r. В
соответствии с 3-м законом Кеплера период
движения по такому эллипсу равен периоду
движения по окружности радиусом r/2, который
найдём из 2-го закона Ньютона:
Найдём время
падения частицы на центр (конечное расстояние до
центра пренебрежимо мало по сравнению с
начальным, т.к. плотность возрастает на много
порядков). Заменим движение по прямой движением
по очень узкому эллипсу с большой осью r. В
соответствии с 3-м законом Кеплера период
движения по такому эллипсу равен периоду
движения по окружности радиусом r/2, который
найдём из 2-го закона Ньютона: 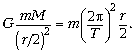
Выразив массу M через начальную плотность облака, найдём время падения на центр:
![]()
Обращаем внимание на то, что ответ не зависит от начального положения частицы в облаке.
3. Два груза массой m каждый соединены нитью длиной l и лежат на гладком столе. Середину нити начинают перемещать горизонтально с ускорением а в направлении, перпендикулярном нити. Какое количество теплоты выделится при неупругом ударе грузов?
Решение. В системе отсчёта,
связанной с серединой нити, на каждый из грузов
действует сила инерции F = –ma,
эквивалентная силе тяжести с ускорением
свободного падения g' = a. Записав для
движения в этом поле закон сохранения энергии ![]() , найдём
количество выделившейся теплоты: Q = mal.
, найдём
количество выделившейся теплоты: Q = mal.
Замечание: утверждение о силе инерции следует из закона сложения ускорений: T = m(a + aотн), откуда T + (–ma) = maотн.
4. Молекула водяного пара при попадании в воду может отразиться, а может и «прилипнуть» – стать молекулой жидкости. Оцените вероятность «прилипания», если известно, что при +20 °С в условиях низкой влажности уровень воды в блюдце понижается за минуту примерно на 1,5 мм (т.е. стакан в час? – Ред.). Давление насыщенных паров при этой температуре составляет приблизительно 2 кПа.
Решение. Насыщенный пар находится в состоянии динамического равновесия с жидкостью, т.е. число «прилипших» молекул равно числу испарившихся. Разумно предположить, что процесс испарения не зависит от наличия пара над поверхностью, а определяется только температурой жидкости. Тогда масса жидкости, испарившейся за время t с поверхности жидкости площадью S, равна
![]()
где ![]() – скорость понижения уровня при низкой
влажности. Для оценки массы молекул насыщенного
пара, упавших за это же время на поверхность,
предположим, что 1/6 часть молекул летит в сторону
жидкости и что все молекулы имеют одинаковую
среднюю скорость
– скорость понижения уровня при низкой
влажности. Для оценки массы молекул насыщенного
пара, упавших за это же время на поверхность,
предположим, что 1/6 часть молекул летит в сторону
жидкости и что все молекулы имеют одинаковую
среднюю скорость ![]() .
За время t поверхности достигнет 1/6 массы
пара, находящегося в цилиндре объёмом S
.
За время t поверхности достигнет 1/6 массы
пара, находящегося в цилиндре объёмом S![]() t:
t: ![]() .
.
Для оценки средней скорости можно
взять значение средней квадратичной скорости ![]() а плотность пара
выразить через давление:
а плотность пара
выразить через давление: ![]()
Подставляя числовые значения, получим:
![]()
5. Один моль идеального газа находится при температуре 300 К. Его объём увеличивают в 5 раз так, что теплоёмкость газа постоянна и равна 5000 Дж/К. Оцените, на сколько изменится температура газа.
Решение. Теплоёмкость газа тем выше, чем ближе процесс к изотермическому. Поскольку молярная теплоёмкость в данном процессе во много раз (почти на три порядка) больше R, сделаем оценку количества полученной теплоты, считая T = const:
![]()
Изменение температуры газа равно ![]() При таком
При таком ![]() T изменение
внутренней энергии, которым мы пренебрегли при
расчёте теплоты, составляет 10–20 Дж (в
зависимости от типа газа), т.е. вносит поправку в
доли процента.
T изменение
внутренней энергии, которым мы пренебрегли при
расчёте теплоты, составляет 10–20 Дж (в
зависимости от типа газа), т.е. вносит поправку в
доли процента.
6. Два маленьких шарика, лежащие на гладкой горизонтальной плоскости, соединены невесомой пружиной. Шарики зарядили одноимёнными зарядами, в результате чего пружина растянулась в три раза. Во сколько раз изменилась частота малых колебаний системы?
Решение. Запишем условие равновесия шариков после нанесения на них зарядов:
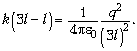
При изменении расстояния между шариками на малую величину x (от 3l до 3l + x) сила взаимодействия изменится на
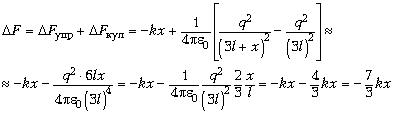
(при упрощении использована первая формула).
Возникающая при малом смещении из
положения равновесия возвращающая сила
эквивалентна действию пружины жёсткостью (7/3)k.
Следовательно, частота колебаний возрастёт в ![]() раз.
раз.
7. Проволочный предохранитель перегорает при напряжении 300 В. При каком напряжении будет перегорать предохранитель, если его длину увеличить в 3 раза, а диаметр в 2 раза?
Решение. Проволочка предохранителя перегорает при достижении температуры плавления. Предполагаем, что нагревание происходит достаточно медленно, т.е. в каждый момент времени мощность выделенного током джоулева тепла равна мощности отдачи тепла в окружающую среду. Мощность теплообмена пропорциональна разности температур и площади поверхности. Получаем
![]()
Отсюда ![]() U2 = 636 В.
U2 = 636 В.
Устный командный тур
1. Прямоугольный брусок, высота которого значительно превышает его длину и ширину, стоит на горизонтальной поверхности. Как определить коэффициент трения между бруском и поверхностью, имея лишь один измерительный прибор – линейку?
Ответ. Надо определить, на какой
максимальной высоте h (отсчитывая от
основания) надо приложить к бруску
горизонтальную силу, перпендикулярную боковой
грани, чтобы брусок скользил, не опрокидываясь.
Тогда ![]() (a –
длина ребра, параллельного приложенной силе).
(a –
длина ребра, параллельного приложенной силе).
2. Конькобежец решил затормозить и свёл вместе пятки, а носки расставил врозь (обычно тормозят наоборот). Как он будет двигаться дальше, если будет продолжать удерживать ступни в этом положении?
Ответ. Описанное положение неустойчиво по отношению к повороту. Конькобежца развернёт, и он поедет пятками вперед.
3. Уровень воды, попавшей в лодку, совпадает с уровнем воды в озере. Где уровень воды будет выше, если в лодку бросить полено?
Ответ. В лодке. С учётом толщины бортов площадь внешнего сечения больше, чем внутреннего.
4. Моллюск выращивает
жемчужину, причём скорость увеличения её радиуса
обратно пропорциональна квадрату радиуса ![]() . За первый месяц
радиус достиг 0,5 мм. Через сколько месяцев
после этого радиус станет 1 мм?
. За первый месяц
радиус достиг 0,5 мм. Через сколько месяцев
после этого радиус станет 1 мм?
Ответ. Скорость нарастания объёма
постоянна: ![]() Объём должен увеличиться в 8 раз, что произойдёт
через 7 месяцев.
Объём должен увеличиться в 8 раз, что произойдёт
через 7 месяцев.
5. Стенки сосуда, заполненного газом с температурой T, быстро нагрели (или охладили) до температуры T1. Что произойдёт с давлением газа?
Ответ. При увеличении температуры стенок давление возрастает, т.к. средняя скорость молекул после удара о стенку становится больше, и переданный импульс увеличивается.
6. Открытая с концов длинная трубка высовывается из воды на 10 см. Верхний конец трубки закрывают, после чего воздух в трубке нагревают от 20 до 100 °С. Оцените, на сколько надо при этом переместить трубку вверх, чтобы уровень воды в трубке остался на уровне воды в сосуде.
Ответ. Давление пара при 100 °С
равно 1 атм, и полное давление внутри будет
больше внешнего на величину давления воздуха в
трубке. Уровень воды в трубке всегда будет ниже.
7. Деревянное кольцо (пяльцы) помещают вертикально на открытую бутылку, а сверху аккуратно ставят вертикальный узкий цилиндр. как, не дотрагиваясь до цилиндра, переместить его внутрь бутылки?
Ответ. Надо резко ударить тяжёлым предметом по внутренней поверхности кольца. При ударе кольцо деформируется, его вертикальный размер уменьшится, и оно вылетит, не успев сообщить цилиндру горизонтальный импульс.

8. Имеется некоторая масса воды при температуре T и другая такая же масса воды при температуре 2T. Можно ли сделать так, чтобы температура всей первой массы воды стала больше, чем температура всей второй массы? Теплообмен с другими телами запрещён.
Ответ. Можно: 1) взять часть (половину) холодной воды и привести её в тепловой контакт с горячей водой (без перемешивания); 2) привести горячую воду в тепловой контакт со второй половиной холодной воды; 3) смешать обе половины холодной воды.
9. Как изменится период колебаний математического маятника, если в точку подвеса и на грузик поместить одноимённые заряды?
Ответ. Не изменится. Кулоновская сила направлена вдоль нити и не даст вклада в возвращающую силу.
10. По торцу длинного стеклянного цилиндра ползает муха, а на боковой поверхности сидит паук. Где должен находиться паук, чтобы он мог увидеть муху? Показатель преломления стекла 1,5.
Ответ. Поскольку предельный угол меньше 45°, вошедшие через верхнюю грань лучи не выйдут через боковую поверхность. Паук не увидит муху.
ИСТОРИЯ НАУЧНЫХ ИДЕЙ И ОТКРЫТИЙ
Устный командный тур
1. Это понятие родилось в Древней Греции. Его древнегреческое название всем хорошо известно. Древнеримские философы придумали для него термин «квинтэссенция». Через 2000 лет, в XIX в., это понятие, зазвучавшее снова на греческом, широко использовалось в физике, однако впоследствии физики дружно от него отказались. Как мы называем (по-гречески) это понятие? Как оно переводится на русский язык? Какой философ впервые ввёл его для объяснения мира и когда (с точностью до века)? Как переводится на русский язык «квинтэссенция» и почему древнеримские философы так его назвали? Под влиянием работ какого учёного физики начали отказываться от этого понятия? Когда (хотя бы приблизительно) это произошло?
Ответы. Эфир; сиять, сияние; Аристотель, IV в. до н.э.; «пятая сущность», поскольку Аристотель добавил её к четырём ранее принятым элементам мира (огонь, вода, воздух, земля); А.Эйнштейн, 1905 г., СТО отменила эфир за ненадобностью.
2. Размеры земного шара впервые определены греком. Когда (с точностью до века) это произошло? Назовите имя этого грека. Где это было (современное название страны)? Что именно и каким прибором измерял этот грек? Как по измеренным данным он вычислял радиус Земли? Какие ещё величины ему были нужны для расчёта?
Ответы. III в. до н.э.; Эратосфен; Арабская Республика Египет; высоту отвесного шеста, врытого в землю, длину тени от шеста – с помощью линейки; измерения проводились в Александрии и Асуане одновременно – в день летнего солнцестояния, в полдень; базовое расстояние от Александрии до Асуана.
3. 29 мая 1919 г. полоса полного солнечного затмения проходила по Южной Америке и Атлантическому океану. Для наблюдения за этим явлением были снаряжены две необычные экспедиции. Один из физических результатов наблюдений получил широчайшую огласку в прессе и известность среди людей, весьма далёких от физики. С именем какого учёного связана известность этих наблюдений? Что конкретно измерялось в этих экспедициях? Какую теорию подтвердило одно из наблюдений? Какие другие экспериментальные факты подтверждают эту теорию? Какое значение имеет эта теория для современной человеческой деятельности?
Ответы. С именем А.Эйнштейна; точные угловые координаты положения звёзд около солнечного диска, закрытого Луной; измерения подтвердили величину отклонения лучей света полем тяготения Солнца, предсказываемую общей теорией относительности; аномальная прецессия орбиты Меркурия (большая по сравнению с предсказываемой ньютоновской теорией тяготения), красное смещение спектров, испущенных массивными небесными объектами, добавочное к доплеровскому смещению; научно-познавательное – на ОТО основаны современные представления о Вселенной, необходимая точность расчётов движения спутников и ракет в околоземном пространстве требует использования не ньютоновской теории тяготения, а ОТО.
4. Деление тяжёлых ядер широко используется в современной энергетике, и не только в ней. Какой учёный (будущий нобелевский лауреат) и когда впервые осуществил этот процесс в лаборатории (хотя и неправильно его интерпретировал)? Какие учёные (один из них – будущий нобелевский лауреат), повторив эти опыты, дали им правильное объяснение и поэтому считаются первооткрывателями явления? Когда и где (страна, город) впервые заработал ядерный реактор? Когда и где (страна, город) заработала первая промышленная атомная электростанция (мощностью 5 МВт)? В каком государстве в наше время ядерная энергетика занимает ведущее место (свыше 75%) в получении энергии?
Ответы. Энрико Ферми, 1934 г., Нобелевская премия 1938 г.; О.Ган и Ф.Штрассман, 1938 г., О.Ган – Нобелевская премия по химии, 1944 г.; США, Чикаго, 1942 г.; СССР, Обнинск, 1954 г.; Франция.
5. Одному великому физику в 58-летнем возрасте пришлось совершить необычное путешествие. Сначала – тёмной ночью через морской пролив в рыбачьей шхуне. Затем около 1200 км в бомбовом отсеке бомбардировщика (потеряв при этом сознание из-за кислородного голодания). Только после этого путешествие проходило комфортабельно – на океанском лайнере и в трансконтинентальном экспрессе. Кто был этот учёный? Укажите маршрут путешествия (страны, города) – начальный, промежуточные и конечный пункты. Когда это было? Каковы были причины этого путешествия? Перечислите основные научные достижения этого учёного.
Ответы Нильс Бор; Копенгаген (Дания) – Мальмё – Стокгольм (Швеция) – Северная Шотландия – Лондон (Англия) – Нью-Йорк – Лос-Аламос (США); октябрь–декабрь 1943 г.; бегство из Дании, захваченной Гитлером, и помощь в создании ядерного оружия в США; квантовая теория атома водорода (1913), теория электронных оболочек и первое приближённое обоснование Периодической системы элементов (1923), принцип дополнительности (1927), первая теория атомного ядра (1936), первая теория деления ядер (1939).