МЕТОДИЧЕСКИЕ
СТРАНИЦЫ
Проф. Н.Н.ТУЛЬКИБАЕВА,
г. Челябинск
К методам решения задач
Первой решается задача, условием
которой заданы все процессы, происходящие с
телами в результате теплообмена.
Анализ и процесс решения задачи
1. В теплообмене участвуют три тела:
пар, лёд и калориметр.
2. Уравнение теплового баланса в общем
виде:
Qпол = Qотд.
(1)
3. Теплообмен осуществляется в
результате отдачи тепла паром и получения тепла
льдом и калориметром. Отсюда запись уравнения
теплового баланса для данной задачи:
Qл + Qал = Qп.
(2)
4. С каждым из тел происходят
определённые процессы:
– лёд нагревается до 0 °С, плавится, и
полученная ледяная вода нагревается до 24 °С:
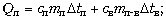
– калориметр нагревается от –8 °С до 24
°С:
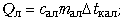
– неперегретый пар конденсируется (100
°С), и образовавшаяся вода остывает до 24 °С:
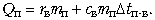
5. Графическая интерпретация
выделенных процессов, в результате которых пар
отдаёт тепло, а лёд и калориметр получают.
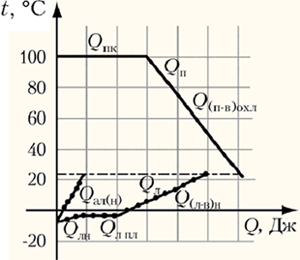
6. Тепловые процессы, происходящие с
каждым телом, изображаются ломаной линией.
Каждый её отрезок представляет определённый
процесс:
– калориметр (алюминиевый)
нагревается: Qал (н);
– неперегретый пар конденсируется,
сконденсированная вода охлаждается: Qпк
+ Q(п-в)охл;
– лёд нагревается, плавится, ледяная
вода нагревается: Qлн + Qл пл
+ Q(л-в)н;
8. Отрезки ломаных линий относительно
оси температуры расположены перпендикулярно (t
= const) или под углом (t 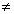 const). Все тепловые процессы
классифицируем относительно изменения
температуры на процессы двух типов:
const). Все тепловые процессы
классифицируем относительно изменения
температуры на процессы двух типов:
– происходящие при постоянной
температуре: плавление (отвердевание) и
испарение (конденсация);
– происходящие при изменении
температуры: нагревание и охлаждение.
Первые процессы аналитически
описываются общей формулой Q = km, где k
– это 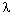 или r.
Вторые процессы – формулой Q = cm
или r.
Вторые процессы – формулой Q = cm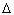 t.
t.
9. Уравнение теплового баланса из
описания всех процессов для тел, участвующих в
теплообмене:
Qпк + Q(п-в)ох = Qалн
+ Qлн+ Qлпл + Q(л-в)н;
(3)
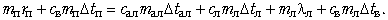 (4)
(4)
10. Решение уравнения (4) относительно mл:
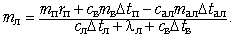
11. Проверка правильности решения в
общем виде по размерности:
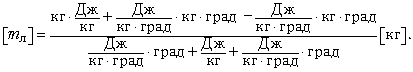
12. Выполнение расчётов:
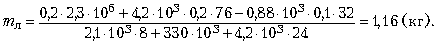
В калориметре находилось 1,16 кг льда.
Работа с задачей, для решения которой
сразу применить уравнение теплового баланса
нельзя. Прежде должно быть проверено условие
применимости уравнения теплового баланса, т.е.
выяснено, заданы ли все процессы, происходящие с
телами. Уравнение теплового баланса есть частный
случай закона сохранения энергии для тепловых
процессов. Его можно применять при решении задач,
если точно определены все процессы изменения
агрегатных состояний тел, участвующих в тепловых
обменах. Одной из первых поэтому должна быть
задача, решение которой без проверки данного
условия невозможно. В ходе проверки необходимо
точно определить все процессы изменения
агрегатных состояний тел и только тогда
применить уравнение теплового баланса.
Основными методами решения может быть перебор
всех возможных ситуаций и сужение области поиска
нужной ситуации. Рассмотрим данный подход (а он
единственно возможный) на примере решения
конкретной задачи.
Комментарии к решению. В тепловом
обмене участвуют два тела: лёд и вода. В процессе
теплообмена могут измениться агрегатные
состояния и льда, и воды. При этом лёд может
растаять, а вода замёрзнуть. Абсолютное
большинство старшеклассников начинают сразу с
записи уравнения теплового состояния, не
учитывая изменения агрегатных состояний тел.
Более того, оказывается неусвоенным само условие
применимости уравнения теплового баланса.
Анализ направленности возможных
процессов при теплообмене данных тел необходимо
начать с выделения всех возможных конечных
ситуаций (рис. 2).
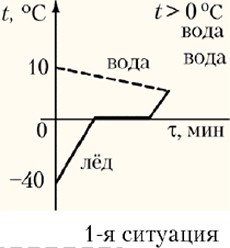
– 1-я ситуация: установится
положительная температура (t > 0 °С);
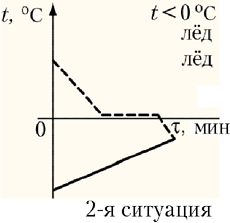
– 2-я ситуация: установится
отрицательная температура (t < 0 °С);
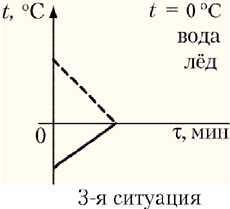
– 3-я ситуация: установится
нулевая температура, при этом вода охладится до
0 °С, и лёд нагреется до 0 °С (t = 0 °С);
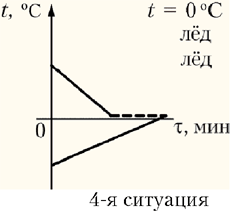
– 4-я ситуация: установится
нулевая температура, при этом вода охладится до
0 °С и вся превратится в лёд, а лёд нагреется до
0 °С (t = 0 °С);
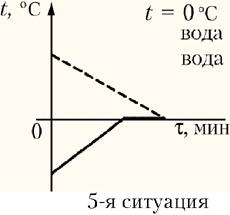
– 5-я ситуация: установится
нулевая температура, при этом вода охладится до
0 °С, лёд нагреется до 0 °С и весь расплавится (t
= 0 °С);
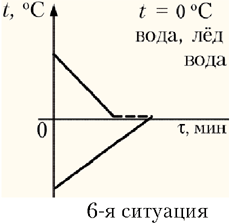
– 6-я ситуация: установится
нулевая температура, при этом вода охладится до
0 °С и частично превратится в лёд, а лёд
нагреется до 0 °С (t = 0 °С);
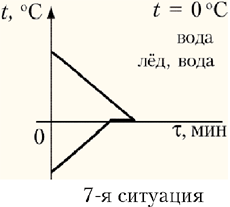
– 7-я ситуация: установится
нулевая температура, при этом вода охладится до
0 °С, лёд нагреется до 0 °С и частично
расплавится (t = 0 °С).
Для наглядности выделенных ситуаций
воспользуемся графической интерпретацией
процессов. Теперь выделены все возможные
ситуации, в каждой заданы процессы изменения
агрегатных состояний тел. Для решения задачи
можно применить метод перебора ситуаций, и для
каждого конкретного случая записать уравнение
теплового баланса. Но для оптимизации решения
можно сузить область поиска. Для этого
необходимо проанализировать все семь выделенных
ситуаций и классифицировать их. Очевидно, эти
ситуации можно разделить на три типа: t > 0
(1-я ситуация), t < 0 (2-я ситуация) и t = 0
(3–7-я ситуации).
Далее надо оценить реальность
ситуаций. Для этого сравним количество теплоты,
выделяемое водой при охлаждении до 0 °С, и
количество теплоты, поглощаемое льдом при
нагревании до 0 °С:
лёд поглощает энергию 50 400 Дж: 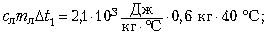
вода отдаёт 16 800 Дж: 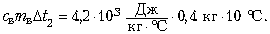
Первый вывод: положительной
температуры не может быть.
Оценим второй тип ситуации, когда t
< 0 °С и необходима дальнейшая отдача тепла
водой. Это может быть при замерзании воды. Пусть
вся вода застынет. При этом выделится 132 000 Дж: 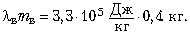
Так как 16 800 Дж + 132 000 Дж > 50 400 Дж, то вся
вода не превратится в лёд.
Второй вывод: отрицательной
температуры не может быть.
Третий вывод: установится температура
0 °С, при этом часть воды превратится в лёд (6-я
ситуация).
Решение задачи можно продолжить и
определить количество застывшей воды: 33 600 Дж = 50
400 Дж – 16 800 Дж должно быть выделено за счёт
отвердевания воды при 0 °С. Поэтому можем
записать:
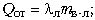 33 600
Дж
33 600
Дж  3,3
3,3 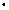 105 Дж/кг
105 Дж/кг 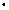 0,1
кг.
0,1
кг.
Итак, при установившейся температуре 0
°С в лёд превратится 0,1 кг воды. Смесь будет
состоять из 0,7 кг льда (0,6 кг + 0,1кг) и 0,3 кг воды (0,4
кг – 0,1 кг). Но интерес представляет решение на
основе уравнения теплового баланса после выбора
соответствующей (6-й) ситуации. Запишем уравнение:
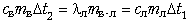
и решим его относительно mв-л: