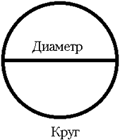
МЕТОДИЧЕСКИЕ
СТРАНИЦЫ

Проф. М.Д.ДАММЕР,
ЧГПУ, г. Челябинск dammermd@yahoo.com

Пропедевтику физики – с начальной школы

В челябинском лицее № 11 с 1998 г. ведётся пропедевтическое изучение физики в 1–6-м классах. Сначала это был эксперимент, охватывающийлишь систему дополнительного образования в 5–6-м классах, потом в этих классах был введён и основной пропедевтический курс физики. В процессе работы мы поняли, что требуется пересмотр содержания естественнонаучного образования начиная уже с 1-го класса. Поэтому вскоре мы расширили свой эксперимент, разработали содержание, новые методы и формы обучения элементам физики в начальной школе. Таким образом, за экспериментальная работа шла в направлении как углубления достигнутых результатов, так и расширения сферы эксперимента. Но начнём всё по порядку.

Одним из результатов современных реформ образования является существенное изменение содержания образования в целом и естественнонаучного, в частности: новые учебники, новые программы. Характерные особенности – повышение научного уровня преподавания, изучение вопросов современной науки, обогащение учебного материала сведениями из истории и методологии науки, изменение традиционной последовательности изучения разделов курсов. Курс физики основной школы стал двухступенчатым. Первая ступень охватывает 5–6-й классы, при этом в подавляющем большинстве школ изучаются интегративные курсы типа «Естествознание», «Природоведение», «Окружающий мир» и т.д., вторая ступень – 7–9-й классы (базовый курс). Однако наряду с положительными переменами усилились и негативные тенденции нарушения преемственности в обучении: обновлённый курс биологии требует более серьёзной подготовки учащихся по физике и химии.

В 5–6-м классах ученики теперь на уроках биологии рассматривают химический состав клетки (органические и неорганические вещества), различные виды движения, силы (включая подъёмную силу, действующую на крыло птицы), давление, движение жидкостей. Это достаточно сложные вопросы, но программа 5-го класса не обеспечивает понятийного базиса для их изучения. Аналогичная ситуация наблюдается с курсом географии: на уроках рассматриваются атмосферное давление, конвекционные потоки, климат и климатические зоны и т.д., что не соответствует подготовке учащихся по физике в рамках курса естествознания. Зато курсы естествознания дублируют материал, изучаемый на уроках биологии, тем самым приводя к перегрузке учащихся.

Пропедевтика естественнонаучных знаний начинается ещё в начальной школе. Однако в учебниках по предметам естественного цикла основной школы мало учитываются знания, полученные учениками на этом этапе.

Таким образом, несогласованность программ курсов естественнонаучного цикла, неправильная последовательность их изучения, во-первых, нарушает преемственность естественнонаучного образования, а во-вторых, приводит к ненужному дублированию некоторых вопросов. Всё это вызывает существенную перегрузку учащихся, усиливающуюся тем, что биологические и географические явления ученики понять просто не в состоянии. В результате достаточно рано наблюдается падение интереса к предметам естественнонаучного цикла. Проблема особенно важна для лицеев.

Другой существенный недостаток современной системы естественнонаучного образования – отсутствие взаимодействия между предметами естественного цикла: жизнь и развитие живых организмов, процессов их жизнедеятельности рассматриваются без учёта физико-химических факторов в среде их обитания и процессов, происходящих внутри самих организмов. Это мешает формированию у учащихся единой естественнонаучной картины мира, раскрытию общности методов исследования, применяемых в естественных науках.

Для преодоления перечисленных недостатков академиком А.В.Усовой была разработана новая концепция естественнонаучного образования. Основным условием для её реализации является пересмотр содержания естественных предметов и опережающее изучение физики с 5-го класса, а химии – с 6-го. В рамках этой идеи были разработаны опережающие курсы физики (М.Д.Даммер), химии (М.Ж.Симонова), биологии (С.М.Похлебаев и В.С.Елагина). Эксперимент по внедрению ведётся с 1994 г. в Челябинске (школы № 80, 99, 102, 124), Аше (школа № 4), Сатке (школа № 10) и Омске (частная школа Альфа-омега).

На этих же идеях базируется пропедевтика физики в лицее № 11. Особенностью лицея как вида учебного заведения является ранняя (с 8-го класса) профилизация обучения. В таких условиях обеспечение сознательного выбора профиля учащимися, своевременное выявление учеников, обладающих склонностями к изучению физики, заинтересованных в деятельности учёного-естествоиспытателя, возможно лишь на основе чётко продуманной системы естественнонаучного образования, соответствия его содержания современному уровню науки, пропедевтики физических знаний на начальных этапах естественнонаучного образования. Развитию творческих способностей школьников должно способствовать взаимодействие двух компонент системы образования — основной и дополнительной.

Целью исследовательского проекта являлась разработка и внедрение курса физики 5–6-го классов, обеспечивающего понятийную базу для изучения других предметов естественного цикла, а также пересмотр содержания естественнонаучного образования в начальной и основной школе, обеспечение преемственности в формировании естественнонаучных понятий и учебно-познавательных умений учащихся. Особенностями курса физики являются:

1. Богатство и разнообразие содержания, включение элементов логики, методологических и межпредметных знаний, сведений из истории науки и техники, прикладных и экологических знаний. Опишем некоторые элементы перечисленных знаний.

Приступая к изучению физики, школьники знакомятся с новой терминологией, овладевают незнакомыми формами мышления. Это очень сложный процесс, и зачастую ученики ориентируются в нём интуитивно. Знания из формальной логики способствуют ориентации школьников в системе научных знаний: они учатся правильно строить определения понятий, формулировать выводы по результатам исследований, выстраивать последовательную цепь суждений, проводить классификацию. Одновременно эти знания являются средством развития мышления и речи.

К методологическим относятся знания о структуре научных знаний и их отдельных элементов. Они способствуют не только сознательному усвоению предметного материала, на их основе проводятся обобщение и систематизация знаний, формирование познавательных умений учащихся. Знания из истории науки раскрывают эволюцию развития физических идей, этапы становления науки. Будучи органично связаны с основным предметным материалом, они всегда эмоционально окрашены и «очеловечивают» научные знания, способствуют становлению современной научной картины мира, формированию мировоззрения учащихся, положительных мотивов учения, воспитанию их нравственных качеств, формированию гуманистических взглядов на окружающую действительность. Воссоздание в классе исторической ситуации по определению физической закономерности в «квазиисследовательской» (термин Г.М.Голина) форме способствует развитию творческих способностей учащихся, формированию у них уверенности в свои силы, возникновению желания мыслить нестандартно, выходя за рамки обыденного.

В комплекс межпредметных могут привлекаться знания из математики, природоведения, химии, биологии, географии и др. Опережающее изучение физики создаёт условия для значительного повышения эффективности межпредметных связей, для осознания взаимосвязи наук и места физики в естествознании. При изучении физики сведения из других областей естествознания способствуют конкретизации общих понятий, а также иллюстрации применения физических знаний в этих областях, иллюстрации общности физических законов и теорий.

Комплекс прикладных знаний объединяет описание различных технологий, устройства и принципа действия приборов и технических устройств, описание ведущих отраслей техники, использующих законы физики, достижения современной астрономии и космонавтики. Они способствуют осознанию роли науки в современном обществе как непосредственной производительной силы; осознанию ценности физических знаний и тем самым формированию положительных мотивов учения, развитию творческого мышления учащихся.

Рассмотрение вопросов техники неизбежно подводит к изучению связанных с ними вопросов экологии. Знакомство учащихся со способами взаимодействия человека с окружающей средой, с необходимостью учёта как положительных, так и отрицательных сторон этого взаимодействия, показ преимуществ экологически чистых технологий способствует формированию ценностных отношений к окружающей действительности, воспитанию моральных качеств личности. При изучении комплекса экологических знаний в курсе физики ученики должны осознать следующие идеи оптимизации экологических взаимодействий: естественнонаучную, связанную с сохранением окружающей среды, и технологическую, направленную на сохранение оптимальной полноты обмена и круговорота веществ, потока энергии и информации. В комплекс экологических входят также знания об охране жизни и здоровья человека — валеологические знания.

Сведения из истории науки, прикладные и экологические знания в значительной степени отражают и региональные особенности. Тем самим эти виды знаний способствуют реализации регионального компонента содержания физического образования.

Содержание пропедевтического курса физики максимально адаптировано для изучения младшими школьниками. В нём явления описываются на качественном уровне, практически полностью исключен математический аппарат.

2. Разнообразие способов учебной деятельности

При изучении пропедевтического курса физики ученики овладевают способами следующих видов деятельности:

– познавательной – работа с учебником и дополнительной литературой; восприятие (восприятие пространства, оценка расстояний, пространственных размеров тел; восприятие времени, оценка длительности временного интервала, временной последовательности событий и др.); наблюдение; эксперимент;

– практической – работа с приборами и принадлежностями; измерения; наглядно-графическая деятельность; решение задач;

– организационной – планирование различных видов деятельности; организация рабочего места и др.;

– оценочной – оценка значимости и ценности информации, экологического состояния окружающей среды, экологических параметров и безопасности технологических процессов, значений физических величин, числовых параметров различных процессов;

– деятельность самоконтроля – контроль правильности и эффективности своих действий, их последовательности и содержания; результатов своей деятельности и др.

3. Структура пропедевтического курса физики. Структура нашего курса можно рассмотреть в двух разрезах — вертикальном и горизонтальном. Вертикальный разрез отражает последовательность изучения отдельных частей курса, горизонтальный – сочетание различных форм обучения (основного и дополнительного) в одной параллели.

В вертикальной структуре курса физики выделены пропедевтическая и основная части (7–9-й классы). Пропедевтическая часть, в свою очередь, состоит из двух подсистем: пропедевтика элементов физических знаний в рамках курса начальной школы «Окружающий мир» и систематический пропедевтический курс физики 5–6-го классов.

В пропедевтической части изучаются наиболее общие понятия (предмет физики и т.д.), физические формы движения материи (механическая, тепловая, электромагнитная) и наиболее общие естественнонаучные понятия (вещество, масса, сила, энергия). Логика изучения различных физических форм материи отражает структуру науки: сохранён последовательный ряд физических форм движения материи; 2) отражено направление научного познания – накопление и анализ эмпирических фактов; введение новых понятий; установление законов и эмпирических закономерностей; объяснение ряда сходных фактов на основе установленных закономерностей; анализ возможностей практического использования полученных знаний.

4. Учебные пособия по пропедевтическому курсу физики объединяют в себе функции учебника (источника информации) и рабочей тетради (организации учебной деятельности школьников). Каждый параграф по возможности отражает завершённый цикл познания. В нём мотивируется целесообразность рассмотрения нового явления (свойства тел), ставится проблема, рассматриваются внешние признаки и условия наблюдения явления, проводится самостоятельное исследование учащимися для установления эмпирических закономерностей явления. После этого рассматриваются примеры явления в природе и технике, объясняются некоторые факты на основе установленных закономерностей.

В учебных пособиях большое внимание уделяется формированию у школьников физических понятий и учебных умений. С этой целью после каждого параграфа приводятся задания для самостоятельной работы в классе и дома. Они построены с учётом психологических закономерностей, в соответствии с этапами формирования физических понятий и учебных умений. В учебных пособиях большое внимание уделяется выполнению опытов и наблюдений (они присутствуют практически в каждом задании), домашнему экспериментированию. Отдельные подзадания даются в нескольких вариантах, а ученикам предоставляется возможность выбора варианта.

5. Взаимодействие основного и дополнительного образования. Наиболее существенной характеристикой лицейской системы физического образования является взаимодействие двух его обозначенных выше подсистем. Содержание обоих представляет собой систематические курсы, в которых изучение одних и тех же физических форм движения материи совмещено по времени. Отличаются они по уровню рассмотрения элементов знаний, а также уровню формируемых способов деятельности. Учебная деятельность в подсистеме дополнительного образования обладает свойствами творческой исследовательской деятельности.

Приведём в качестве примера учебно-методические материалы, разработанные совместно с молодым учителем лицея № 11 Верой Владимировной Хохловой (даются в сокращении. – Ред.).

ИЗМЕРЕНИЕ ДЛИНЫ И ПЛОЩАДИ

<...>

Экспериментальные задания

<...> 11. Измерьте площадь фигуры кита-белухи на рисунке с помощью палетки.

Кит-белуха

Вспомните, как измерить площадь неправильной фигуры c помощью палетки.

С (цена деления палетки) __________

N (число полных квадратов) _______

M (число неполных квадратов) ______

S (площадь фигуры) = C (N + М : 2) 2

S =

Ответ: площадь фигуры равна ____________

12. Измерьте длину окружности.

Указания

– Вырежьте из бумаги 3 круга любого диаметра.

– Обозначьте на них диаметр.

– Возьмите нитки и аккуратно обведите ими круг по краю – по окружности. Сделайте на нитке отметку для точного определения её конечного положения.

– Измерьте длину нитки до отметки. Результат занесите в таблицу.

– Измерьте диаметр окружности. Результат занесите в таблицу.

– Найдите отношение длины окружности к диаметру.

– Сформулируйте вывод: как зависит длина окружности от диаметра?

Вывод:_______________________________

Можно предложить и другой выход. Курвиметр – прибор весьма простой, его можно изготовить самостоятельно. Простейшая конструкция – проградуированный диск с указателем, вращающийся вокруг центра. Придумайте, как сделать такой курвиметр. Попробуйте сделать его и проведите измерения.

Из истории метра

Материал для дополнительного чтения

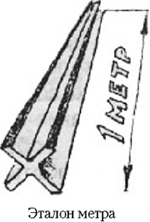
В учебнике математики вы уже читали, что в старину длину измеряли не метрами или сантиметрами, а другими единицами. Эти единицы были связаны с размерами тела человека. Конечно, пользоваться такими единицами удобно – они всегда под рукой. Но, с другой стороны, у каждого был «свой аршин». Правда, со временем единицы были стандартизированы. Например, в Англии и США до сих пор пользуются единицами длины, связанными с размерами тела человека. Но они уже стандартизированы, т.е. все футы одинаковы и равны примерно 30 см, все дюймы одинаковы и равны примерно 25 мм. Тем не менее наличие в каждой стране своих единиц длины создавало определённые неудобства в развитии торговли, обмене научной информацией и т.д. Поэтому учёные пришли к выводу, что во всём мире нужны одинаковые единицы длины и других физических величин. По предложению Парижской академии наук в 1791 г. (во времена Французской буржуазной революции) за единицу длины была принята одна сорокамиллионная часть парижского географического меридиана. Эту единицу назвали метром (по-гречески это означает мера). Был изготовлен эталон в виде платиновой линейки шириной 25 мм, толщиной 4 мм и длиной 1 м.

Со временем длина меридиана была точно измерена, и оказалось, что изготовленный эталон не соответствует одной сорокамиллионной его части. Но в качестве единицы длины всё-таки была оставлена длина изготовленного ранее эталона. По его образцу в 1882 г. был изготовлен новый эталон из сплава платины с иридием, который хранится во французском городе Севре, в Международном бюро мер и весов. А тридцать три копии этого эталона хранятся в разных странах мира. В России хранятся копии № 28 и № 11.

Измерение объёма

Как узнать, сколько зерён риса помещается в стакане? Для ответа на этот вопрос нам понадобится научиться измерять ещё одну важную величину – объём. Дело в том, что у плоских тел (различных фигур) объёма не бывает. Объём является величиной, связанной с пространственными размерами тел. Примером могут служить стакан, зерно риса, тело человека и т.д.

Для измерения объёма надо определить, какое количество кубиков, объём которых принят за единицу, помещается в теле. То есть как бы построить тело из единичных кубиков. К примеру, все вы играли c кубиком Рубика. Для того, чтобы узнать его объём, нужно измерить, сколько цветных кубиков в него входит.

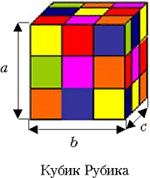
Для этого необходимо перемножить количество кубиков, входящих в его длину, ширину и высоту: V = a b c.

Итак, V_{кубика Рубика} = 3 3 3 = 27 кубиков.

За единицы объёма приняты объёмы кубиков с рёбрами 1 мм, 1 см, 1 дм, 1 м и т.д. Их называют кубическими миллиметрами (1 мм³), кубическими сантиметрами (1 см³) и т.д. Если считать, что ребро кубика Рубика равно 1 см, то его объём удобно выразить в кубических сантиметрах:

V_{кубика Рубика} = 3 3 3 = 27 см³.

Существуют и другие единицы объёма. Объём жидкостей часто измеряют в литрах и миллилитрах, а объём нефти – в баррелях (159 л).

1 л = 1 дм³. 1 л = 1000 мл.

Измерить объём кубика Рубика несложно. А как измерить объём тела неправильной формы? Например, объём камня, ложки, болта и др.?

Объём тела неправильной формы и объём жидкости измеряют с помощью мензурки. Мензурка – это прозрачный сосуд с делениями, указывающими объём налитой в неё жидкости. Чаще всего шкалу мензурки градуируют в миллилитрах.

Измерение объёма твёрдых тел с помощью мензурки производят следующим образом. Сначала наливают в мензурку некоторое количество жидкости и измеряют её объём по шкале, нанесённой на мензурку. Затем погружают в жидкость тело, объём которого нужно измерить. При этом уровень жидкости в мензурке повышается. Теперь нужно измерить по шкале новое значение объёма – жидкости и погружённого в нее тела. И наконец, вычислив разность двух измеренных объёмов, найти объём тела.

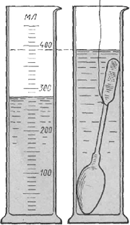
Мензурка с помещённым в неё телом непра-вильной формы

При измерениях мензуркой необходимо учитывать, что у большинства жидкостей уровень приподнят у краев. Поэтому для правильного отсчёта надо расположить глаз точно напротив уровня жидкости и производить отсчёт по средней части её поверхности.

Если измеряют объём тел из веществ, растворяющихся в воде, в мензурку вместо воды насыпают сыпучее вещество (сахарный песок, соль и др.).

Вопросы и задания

1. В каких единицах выражаются соответствующие физические величины? Соедини стрелками.

2. Пользуясь формулой для объёма куба, определите, как соотносятся различные единицы объёма (1 мм³, 1 см³, 1 м³).

3. Сколько кубических сантиметров в одном литре?

4. Как соотносятся 1 мл и 1 см³?

5. Нарисуйте шкалу мензурки с ценой деления 2 мл.

6. У вас имеется коробка канцелярских скрепок. Как измерить с помощью мензурки объём одной скрепки?

7. Как измерить, сколько зёрен риса помещается в стакане?

8. Придумайте, как с помощью мензурки измерить объём тела, если оно не помещается в мензурку, но помещается в чашку. Проведите измерения. Сделайте в тетради поясняющий рисунок.

Экспериментальные задания

9. Возьмите прямоугольный кусочек сахара, измерьте его длину, ширину и высоту. Вычислите его объём. После этого измерьте объём кусочка сахара с помощью мензурки (быстро, пока он не растворился). Сравните два результата. Какой из них более точный?

10. Возьмите бутылку с делениями (например, для детского питания). Налейте в неё воду примерно до  половины. Закройте её плотной пробкой. Придумайте, как, не открывая бутылки, определить её вместимость (объём воды, налитой до горлышка бутылки)? Сделайте поясняющий рисунок и проведите соответствующие измерения. После этого откройте бутылку и проверьте свой результат, измерив вместимость бутылки с помощью мензурки.

11. Измерьте объём твёрдых тел.

Указания:

– Определите цену деления мензурки (С).

– Измерьте объёмы данных вам тел. Результаты занесите в таблицу.

Выводы: _____________________________

ТЕМПЕРАТУРА

В своей жизни вы уже не раз сталкивались со словом «температура». Но может ли кто-нибудь из вас сказать, что оно означает? Этот параграф поможет вам разобраться в этом непростом вопросе.

С латыни слово «temperatura» переводится как надлежащее смешение, правильное соотношение или правильное устройство, нормальное состояние. Раньше его использовали в медицине, и касалось оно только состава лекарств. В настоящее время слово «температура» имеет совсем другой смысл.

Температура – это физическая величина, которая характеризует степень нагретости тела.

Тело с более высокой температурой является более нагретым, а с меньшей – менее нагретым.

Но, как узнать, какая температура у данного тела? Без специального прибора это выполнить практически невозможно, т.к. температуру невозможно увидеть, услышать, обонять. Потрогав рукой утюг, мы точно можем сказать, нагрет он или нет. Но оказывается, этого не достаточно для точного определения значения температуры.

Проведём простой опыт.

Возьмём три глубокие чашки, в одной из которых будет очень холодная вода, в другой горячая, а в третьей вода из графина, длительное время стоявшего в комнате. Подержим некоторое время одну руку в горячей воде, а другую – в холодной. После этого опустим обе руки в тарелку с водой из графина. Почувствуем, что одна и та же вода для одной руки будет теплее, чем для другой. Этот опыт показывает, что ощущение тепла может быть обманчивым, и с помощью чувств нельзя достоверно определить температуру тела.

Здесь нам на помощь приходит специальный прибор – термометр. При изменении температуры тела изменяется какое-либо его свойство, например, объём. На этом и основано действие термометра.

Разные тела при нагревании расширяются по-разному, это необходимо учесть при выборе вещества, используемого в термометре.

Первый термометр был изобретён великим итальянским учёным Галилео Галилеем около 1600 г. В качестве расширяющегося вещества при нагревании в нём использовался воздух. Свой термометр Галилей назвал «термоскопом». Термоскоп состоял из стеклянной трубки с шариком на конце, опущенной в сосуд с водой. По изменению уровня воды в трубке определялось изменение температуры. Так как термоскоп не имел шкалы, то он использовался только для сравнения различных температур.

Первые конструкции термометров

Позже возникла необходимость совершенствования конструкции термометра: в качестве расширяющегося вещества стали использовать жидкость. Такие термометры стали называть жидкостными. Трубка с жидкостью была запаяна, а воздух из неё откачан. Также термометр был снабжён температурной шкалой (для более точного её измерения).

Наибольшее распространение получила шкала, предложенная шведским физиком Цельсием. По этой шкале лёд тает при 0 °С, а вода кипит при 100 °С, промежуток между этими точками делится на 100 частей, каждая из которых считается градусом. Помимо шкалы Цельсия существовало множество других шкал. В число наиболее распространённых шкал входят также шкалы Фаренгейта и Кельвина.

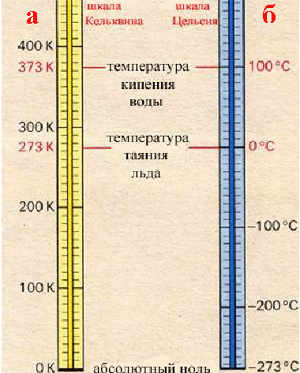
Температурные шкалы Кельвина (слева) и Цельсия (справа)

В 1724 г. голландский физик Фаренгейт предложил шкалу, в которой температура таяния льда равнялась 32 F, а кипения воды 212 F. Один градус по шкале Фаренгейта не соответствует одному градусу по шкале Цельсия. В настоящее время шкалу Фаренгейта используют в Америке. В науке пользуются шкалой абсолютной температуры, введённой Кельвином. Градус по этой шкале совпадает с градусом Цельсия, ноль соответствует температуре, при которой прекращается движение частиц вещества (–273 °С). Эта температура недостижима. Отрицательной температуры по шкале Кельвина не бывает.

Каждый термометр предназначен для измерения температуры лишь в определённых пределах!

Кроме жидкостных термометров существуют манометрические, газовые, термоэлектрические, магнитные, биметаллические и др. термометры.

Размер таких термометров сильно уменьшился, а чувствительность существенно возросла.

Современными термометрами можно измерить температуру небесных тел, определить удаление Земли от Солнца, уловить тепло свечи на расстоянии в 3 км!

Современные термометры

Правила пользования термометром:

1. Необходимо подобрать термометр, чтобы измеряемая температура не выходила за границы установленных для данного термометра предельных значений.

2. Определить цену деления шкалы термометра.

3. Привести термометр в соприкосновение со средой, температуру которой нужно измерить. Подождать какое-то время, пока не наступит тепловое равновесие, т.е. пока температуры не станут равными.

4. Посмотреть показания термометра так, чтобы глаз находился на уровне верхнего конца столбика жидкости термометра. (При этом извлекать термометр из среды не следует. Исключение составляет медицинский термометр).

• Самая высокая температура воздуха на Земле, равная +58 °С, была зарегистрирована в Ливийской пустыне в местечке Эль-Азизия в 1922 г.

• Самая низкая температура воздуха на Земле, равная –88,3 °С, была зарегистрирована советскими полярниками 24 августа 1960 г. в Антарктиде на внутриконтинентальной станции «Восток».

• Температура тела здорового человека равна 36–37 °С.

• Температура на поверхности Солнца равна 6000 °С.

• Гуси, утки и кошки – самые морозостойкие животные: они выдерживают температуру –110 °С, в то время как тюлени – жители полярных морей – погибают при –80 °С, а большинство млекопитающих при –45 °С.

         
Морозостойкие животные

• Оказывается, что уши, хвост, лапы животных тем короче, чем холоднее климат. А температура лапы животного отличается от температуры тела. Например, температура тела белой куропатки может превышать температуру её лап на 38 °С.

Самостоятельное исследование

Давайте смоделируем этот опыт.

Вырежьте из бумаги полоску шириной 2 см и длиной 19 см. Сложите её так, чтобы длина одной стороны оказалась 10 см, а второй – 9 см. Склейте свободные концы полоски.

Почему длинная сторона склеенной полоски изогнулась? Сравните это явление с нагреванием биметаллической пластинки.

Можно ли биметаллическую пластинку использовать для измерения температуры? Как?

Действия, необходимые для вашего опыта:

1. Зажмите в тиски один конец биметаллической пластинки.

2. Другой конец подогрейте над газом.

Что произошло с пластинкой? Что изменится, если пластинка будет состоять из других металлов? Придумайте свой вариант названия биметаллической пластинки.

_________________________________________________________

_________________________________________________________

_________________________________________________________

Выводы:

__________________________________________________________

Подтвердилась ли наша гипотеза? ___________

Дата исследования

Вопросы и задания

1. Вставьте в предложения пропущенные слова.

Термометр – это измерительный …………. С его помощью измеряют физическую величину – …………. Термометр имеет ………, по которой можно определить точное значение температуры.

2. На чём основано действие жидкостного термометра?

3. В чём сходство и различие биметаллического и жидкостного термометров?

4. Достаточно ли точным будет измерение температуры двух миллилитров воды, если оно проводится обычным жидкостным термометром?

5. Почему портится медицинский термометр, если его нагреть до температуры выше 43 °С? Как можно устроить термометр, чтобы он не портился, если его нагреть слишком сильно?

6. Какое вещество используется в медицинском термометре?

7. Почему надо выждать некоторое время, прежде чем сделать отсчёт по шкале при измерении температуры?

8. Для измерения температуры в стакан с водой опустили термометр. Что можно сказать о температуре воды и среды, в которой до этого находился термометр, если показания термометра:

А) не изменилось?

Б) уменьшилось?

В) увеличилось?

9. Определите предельные значения измеряемой температуры и цену деления всех термометров, находящихся у вас дома.

10. Известно, что эмаль и дентин расширяются не одинаково, причём эмаль – вещество хрупкое. Как с этим согласуются предостережения зубных врачей от употребления очень горячей или холодной пищи и воды?

11. Как можно объяснить ситуацию, показанную на рисунке?

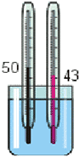
Два термометра в стакане с водой

Манана Дмитриевна Даммер – родилась в г. Тбилиси (Грузия) в семье педагогов. Окончила физический факультет МГУ им. М.В.Ломоносова в 1980 г. и пять лет преподавала физику в челябинской школе № 31, где и начала апробировать свой экспериментальный пропедевтический курс. В 1990 г. защитила кандидатскую диссертацию на тему «Приёмы и средства систематизации знаний учащихся по физике в 7–8-х классах», в 1997 г. – докторскую диссертацию на тему «Методические основы построения опережающего курса физики основной школы». В 1998 г. получила учёное звание профессора кафедры методики преподавания физики ЧГПУ и была избрана действительным членом Академии педагогических наук Грузии. Автор учебников физики для 5–6-х классов – эти учебники победили в открытом конкурсе Грузии и были утверждены Минобразованием Грузии, по ним в этой республике занимаются школьники 7–9-х классов. Последние годы занимается разработкой содержания и методики преподавания курса физики в рамках новой концепции естественнонаучного образования академика А.В.Усовой, проводит собственные исследования, а также руководит исследованиями аспирантов и соискателей по проблеме раннего обучения физике. Постоянно ведёт педагогический эксперимент в школах. Имеет нагрудные знаки «Отличник просвещения» (1996 г.), «Почётный работник высшего профессионального образования» (2004 г.).