Т.С.САМОЙЛОВА, О.Б.ФЕДОСЕЕВ,
школа № 444, г. Москва
Домашние контрольные работы
Тема «Законы сохранения в механике»,
10-й кл. Расширенный курс
В связи с повышением
научно-теоретического уровня обучения возникла
необходимость усилить контроль за качеством
знаний учащихся. Ничто так не активизирует
умственное развитие учащихся, как решение
физических задач. В связи с этим понятна
необходимость проведения контрольных работ,
выполняющих не только контрольную, но и
обучающую функцию. Однако для детей любая
контрольная, проведённая в традиционной форме, –
это стресс. Чтобы снять нервную нагрузку без
ущерба для уровня знаний, мы предлагаем
перенести контрольную работу в комфортную
ситуацию, а именно, в домашние условия. По уровню
предлагаемые контрольные соответствуют задачам
для поступающих в технические вузы (80% – задачи
стандартного уровня и 20% – более высокого).
Учащиеся получают возможность решать задачи в
личном темпе, не ограничивая себя рамками урока и
при необходимости обращаясь за помощью к
преподавателям и родителям. Согласно нашей
гипотезе, домашние контрольные работы
способствуют снятию нервной нагрузки с учащихся
и формированию положительной мотивации к
обучению физике. В итоге повышается уровень
усвоения знаний учащимися.
Преподаватели физики нашей школы
выработали систему отбора задач, определили их
количество, подготовили дидактический материал
по основным темам курса физики, отработали
технологию работы с домашними контрольными
работами. Задачи подбирались так, чтобы можно
было проверить усвоение учащимися основных
знаний и умений по данной теме.
Технология работы следующая. В начале
изучения темы всем желающим раздаются листы с
напечатанными текстами задач, называется срок
сдачи решений учителю (примерно за неделю до
традиционной контрольной работы). Учитель
проверяет домашние контрольные работы, отмечает
номера верно решённых задач, оставляя за
учащимися право сдачи окончательного варианта
работы непосредственно на уроке, во время
проведения традиционной контрольной работы.
Для проверки понимания решённых
домашних контрольных задач можно либо
предложить учащемуся решить во время классной
контрольной работы три-четыре задачи из
домашнего списка, либо организовать защиту
учащимися решённых задач на дополнительных
занятиях. Второй путь – более ёмкий по времени,
однако позволяет ученику видеть результаты
своего труда, исправить ошибки, допущенные в ходе
самостоятельных рассуждений, и т.д.
Пакет домашних контрольных задач
можно также использовать в текущей
индивидуальной урочной и внеурочной работе, в
том числе и для дифференцированных домашних
заданий, и при обобщённом повторении темы.
Приводим пакет таких задач (с ходом
решения) по теме «Законы сохранения» (10-й класс).
1. Два небольших тела, находящиеся на
одной высоте в диаметрально противоположных
точках на краю полусферической чаши радиусом R,
начинают соскальзывать без трения внутрь этой
чаши. Найдите максимальную высоту подъёма тел
после их абсолютно неупругого удара, если
отношение их масс равно 2.
2. Атом распадается на две части
массами m1 и m2 общей
кинетической энергией Ek. Определите
их скорости. Скоростью атома в момент распада
пренебречь.
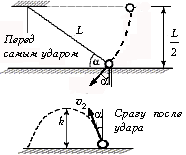
3. Математический маятник с нитью
длиной L первоначально находится в
горизонтальном положении на расстоянии L/2
от горизонтальной стальной плиты. На какую
максимальную высоту поднимется шарик маятника
после абсолютно упругого удара о плиту?
4. Два упругих шарика массами m1
= 8 г и m2 = 20 г подвешены на тонких нитях
длиной соответственно L1 = 10 см и L2
= 6 см так, что они соприкасаются и находятся на
одной высоте. Шарик массой m1 отклонили
на угол 60° от вертикали и отпустили. Считая удар
абсолютно упругим, определите максимальное
отклонение шариков от вертикали после удара.
5. На гладкой горизонтальной
поверхности на некотором расстоянии от
вертикальной стенки находится шар массой M.
Другой шар массой m скользит по направлению
к шару M от стенки. Между шарами происходит
абсолютно упругий центральный удар. При каком
соотношении масс шаров второй шар после удара
достигнет стенки и, упруго отразившись от неё,
достигнет первого шара?
6. В покоящийся клин массой M
попадает горизонтально летящая пуля массой m
и после абсолютно упругого удара о поверхность
клина отскакивает вертикально вверх. На какую
высоту поднимется пуля, если скорость клина
после удара оказалась равной 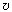 ? Трением пренебречь. Считать,
что после удара клин движется поступательно.
? Трением пренебречь. Считать,
что после удара клин движется поступательно.
7. На стоящий на горизонтальном полу
клин массой М с высоты h падает шар
массой m и отскакивает в горизонтальном
направлении. Найдите скорость клина 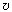 после удара. Считать, что
после удара клин движется поступательно. Трением
пренебречь. Удар шара о клин считать абсолютно
упругим.
после удара. Считать, что
после удара клин движется поступательно. Трением
пренебречь. Удар шара о клин считать абсолютно
упругим.
8. На пути тела, скользящего по
горизонтальной поверхности, находится
незакреплённая горка высотой Н = 2 м. При
какой минимальной скорости тело может
преодолеть горку? Масса горки в 6 раз больше массы
тела. Считать, что тело движется, не отрываясь от
горки, и оба они скользят без трения.
9. Обруч массой m катится по
горизонтальной поверхности без проскальзывания
со скоростью 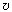 .
Определите кинетическую энергию этого обруча.
Сколько выделится тепла при его полной остановке
(без падения)?
.
Определите кинетическую энергию этого обруча.
Сколько выделится тепла при его полной остановке
(без падения)?
10. Монета скользит по наклонной
плоскости с углом наклона к горизонту 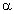 и в точке С имеет скорость
и в точке С имеет скорость
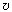 0. Через
некоторое время монета оказалась в точке D
наклонной плоскости, пройдя путь s и
поднявшись по вертикали на высоту Н.
Коэффициент трения скольжения между монетой и
наклонной плоскостью k. Найдите скорость
монеты в точке D.
0. Через
некоторое время монета оказалась в точке D
наклонной плоскости, пройдя путь s и
поднявшись по вертикали на высоту Н.
Коэффициент трения скольжения между монетой и
наклонной плоскостью k. Найдите скорость
монеты в точке D.
11. В цилиндрическом сосуде с водой на
глубине h от свободной поверхности жидкости
есть отверстие. Определите скорость истечения
жидкости из отверстия. 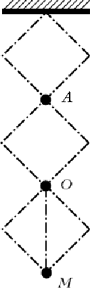
12. Подвеска состоит из стержней
одинаковой длины, соединённых шарнирно. Между
точками O и M натянута нить.
Определите силу натяжения нити OM, если масса
всей системы равна m.
13. К подвеске (см. задачу 12) в точке M
подвешен груз весом P. Какую силу следует
приложить в точке A, чтобы система была в
равновесии? Силой тяжести подвески пренебречь.
14. На теннисный мяч с высоты 1 м падает
кирпич и подскакивает почти на 1 м. На какую
высоту подскакивает мяч?
15. Брусок массой m покоится на
горизонтальной плоскости. К нему прикреплена
недеформированная пружина жёсткостью k.
Какую работу нужно совершить, чтобы сдвинуть с
места брусок, растягивая пружину в направлении,
составляющем угол 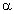 с горизонтом? Коэффициент трения между
бруском и плоскостью
с горизонтом? Коэффициент трения между
бруском и плоскостью 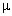 .
.
16. Какой максимальный подъём может
преодолеть тепловоз мощностью W = 370 кВт,
перемещая состав массой m = 2000 т со скоростью 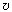 = 7,2 км/ч, если
коэффициент трения k = 0,002? Считать угол
наклона полотна железной дороги к горизонту
малым.
= 7,2 км/ч, если
коэффициент трения k = 0,002? Считать угол
наклона полотна железной дороги к горизонту
малым.
Ответы (и ход решения)
1. Hmax = R/9.
2. 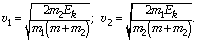
3. 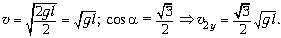
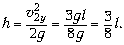
4. cos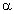 1 = 0,91; cos
1 = 0,91; cos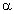 2 = 0,73.
2 = 0,73.
5. Воспользуемся законами сохранения.
Второй шар догонит первый, если 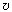 2 >
2 > 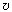 1, т.е.
1, т.е.
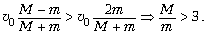
6. 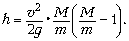
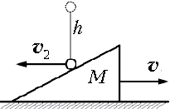
7. 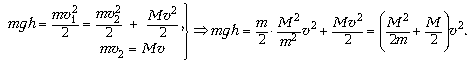
Отсюда 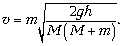
8. 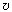 1
– скорость горки в тот момент, когда тело
достигнет её вершины.
1
– скорость горки в тот момент, когда тело
достигнет её вершины.
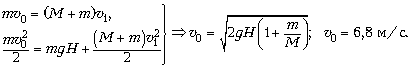
9. E = Q = m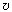 2.
2.
10. ED = Eс + Атр.
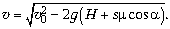
11. Применим закон Бернулли:
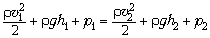 ,
,
где p1 = p2 = pатм,
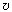 1 = 0, h2
= 0, h1 = h.
1 = 0, h2
= 0, h1 = h.
Отсюда получаем формулу Торричелли: 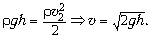
12. При уменьшении длины нити на l
длина всей подвески уменьшается на 3l,
следовательно, центр тяжести поднимается на 1,5l.
Работа силы натяжения нити при этом равна
изменению потенциальной энергии системы. Отсюда
T = 1,5mg.
13. Сместим точку А на 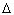 l, действуя силой F.
При этом груз сместится на 3
l, действуя силой F.
При этом груз сместится на 3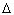 l. Поэтому
l. Поэтому
А = 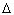 Ep; F
Ep; F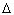 l = P . 3
l = P . 3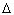 l
l  F = 3P.
F = 3P.
14. В момент отрыва кирпича от мяча
скорость верхней точки мяча и скорость кирпича
одинаковы. Из закона сохранения энергии находим
эту скорость 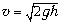 (h
– высота подъёма кирпича).
(h
– высота подъёма кирпича).
Скорость нижней точки мяча при отрыве
от него кирпича равна нулю. Поэтому скорость
центра тяжести мяча равна 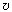 /2.
/2.
Запишем закон сохранения энергии для
кирпича:
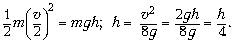
h = 25 см.
15. 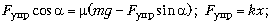
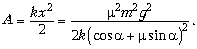
16. 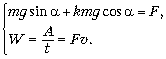
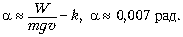
Литература
Баканина Л.П., Белонучкин В.Е., Козел
С.М., Колачевский Н.Н. и др. Сборник задач по
физике. – М.: Наука, 1971.
Балаш В.А. Задачи по физике и
методы их решения. – М.: Просвещение, 1983.
Бендриков Г.А., Буховцев Б.Б.,
Керженцев В.В., Мякишев Г.Я. Задачи по физике
для поступающих в вузы. – М.: Наука, 1998.
Буховцев Б.Б., Кривченков В.Д.,
Мякишев Г.Я., Сараева И.М. Сборник задач по
элементарной физике. – М.: Наука, 1974.
Гельфгат И.М., Генденштейн Л.Э., Кирик
Л.А. 1001 задача по физике с решениями. – М.:
Рубикон, 1997.
Гольдфарб Н.И. Задачник по физике.
9–11 классы. – М.: Дрофа, 2000.
Коган Б.Ю. Задачи по физике. Пособие для
учителей. – М.: Просвещение, 1971.