лицей «Профессионал», г. Харьков, Украина vepsht@yahoo.com «Непредметное (вне-, над-, сверх-, запредметное) ядро содержания образования»Опыт конструирования
Г.П.Щедровицкий. «Языковое мышление» и методы его исследования: Автореферат диссертации на соискание учёной степени кандидата философских наук. – М., 1964.
В.Г.Богин. СТАТЬЯ?– Приведённые отрывки свидетельствуют: проблемы оптимизации школьного образования давно находятся в фокусе внимания специалистов. Значимых тенденций решения указанной задачи, однако, не наблюдается. Подсчёт дидактических единиц, которые должны усвоить дети по предметам естественнонаучного цикла и математике, приведённый в статье О.Леонтьевой «Минимум, переполняющий память» («Первое сентября», 02.02.2002), красноречиво демонстрирует указанное обстоятельство. Согласно приведённым в статье результатам исследований, дети только в основной школе и только по указанным предметам должны усвоить более тысячи понятий, определений, правил и т.п. Утверждаю: никто и никогда не доказал, что существует способ усвоения учебного материала в полном объёме большинством учащихся. Во время посещения одной из школ президент России предложил министру образования ответить на вопросы школьной программы по биологии. Результат предсказуем: министр ответить не смог. Разумеется, можно возразить, что «оперативная память» взрослого человека и не должна содержать знания в объёме школьной программы. Достаточно содержать нужную информацию в «постоянном запоминающем устройстве». В результате возникает необходимая «зона компетенции»: тот же министр понимает на должном уровне содержание выступления специалиста, хотя сам сообщения такого рода сделать не может (что, разумеется, и не нужно). Может, и так. Существуют, однако, сигналы, свидетельствующие как раз об отсутствии указанной «зоны», о низкой компетентности населения как в основах научных знаний, так и в социально-политической области. Результат известен: беспрецедентный размах псевдонаучной деятельности, широкие возможности манипулирования сознанием. Либеральная демократия многочисленным ИНЫМ способам организации жизнедеятельности (от тоталитаризма до фундаментализма) не может противопоставить ничего, кроме ОБРАЗОВАННОГО НАСЕЛЕНИЯ. Фокус, однако, в том, что реформы образования на Западе, в России и Украине ставят совершенно разные задачи. Логика реформы, в целом, такова. Школьная программа несъедобна! Многочисленные попытки накормить ею молодую поросль успеха не имели. Так, может, следует «повернуться лицом к населению»? И спросить: «Население! Нужны ли тебе эти пестики с ангидридами, эти синусы с ферромагнетиками?». Народ, как водится, молчит. И в молчании этом каждый может услышать то, что хочет. Можно услышать, к примеру, желание, а можно – и нежелание трудящихся учить детей тому, что «не пригодится». Но как узнать, что именно пригодится, а что – нет? Вот как отвечает на поставленный вопрос идеолог реформы образования в России А.Пинский: «Люди не дураки. И они… “не обязаны быть экспертами, чтобы знать, чего они хотят”» (http://mschools.ru/forum/viewtopic.php?id=16). Это представление кажется мне ошибочным: люди не только решительно не знают, чему и как учить своих детей, но и не скрывают своего незнания. Люди (родители) с радостью переложили бы эту проблему на плечи учителя. Проблема состоит в том, что учитель не знает тоже. Ничего удивительного здесь нет. В повести С.Витицкого (Б.Стругацкий) «Бессильные мира сего» некий педагогический гений творит чудеса. Сверхъестественным чутьём угадывая скрытые таланты любого ребёнка, учитель указывает оптимальный путь развития личности и делает первые шаги в нужном направлении. Замечательная идея (в каждом искра Божья), увы, не более чем сладкая мечта. Хорошо бы, да, видимо, никому не дано угадать замысел Творца. Реальная задача средней школы, на мой взгляд, состоит, увы, лишь в том, чтобы вывести каждого учащегося на высоту принятия решения о дальнейшей профессиональной специализации. В широком смысле, это означает погружение подрастающего поколения в КУЛЬТУРУ, в рамках которой только и теплится надежда на позитивное развитие человеческой цивилизации. В узком смысле, речь идёт о том, чтобы обучить «всех всему». Не следует думать, разумеется, что в средней школе учащиеся проходят предпрофессиональную подготовку по всем возможным направлениям деятельности. Необходимо всего лишь указать тот внерыночный, надрыночный уровень образованности, который соответствует решению тактических и стратегических задач, стоящих перед школой. И здесь возникают две проблемы: 1. Каков минимальный объём знаний, умений и навыков, который необходимо передать учащимся? 2. Как это сделать? Несмотря на многовековую разработку различных аспектов дидактики, внятный ответ на указанные вопросы так и не получен. Не исключена, между прочим, возможность того, что решение проблем такого рода вообще невозможно. Скажем, объём знаний, обеспечивающий преемственность ценностей цивилизации, на некотором уровне её развития подрастающее поколение освоить не в состоянии. Вот тут-то и настанет «закат Европы», уже давно предрекаемый эсхатологически настроенной частью западной интеллектуальной элиты. К счастью, ни доказать, ни опровергнуть это утверждение невозможно. Существует всего два способа справиться с лавиной информации: модернизировать способ её усвоения и упорядочить содержание. Несмотря на колоссальное количество научных исследований в области дидактики, следует прямо сказать, адекватных способов усвоения растущего объёма информации педагогика не предложила. По меткому выражению проф. В.В.Гузеева (Методы и организационные формы обучения. – М.: Народное образование, 2001), «дидактика и ныне мало отличается от той, что была создана гением Я.А.Коменского». Содержание образования вообще оказывается вне зоны обсуждения. Исследования, которые начинаются философским анализом ситуации, «вниз», к конкретным решениям, не опускаются. Авторы же, разрабатывающие пресловутые «межпредметные связи», как правило, демонстрируют лишь механическое соединение элементов родственных курсов и, таким образом, не «поднимаются» до того уровня обобщений, который требуется. Между тем совершенствование содержания образования – это, похоже, единственная задача, которая не только должна, но и может быть успешно решена. Рискую предложить вниманию читателя попытку «поднятия» темы до небходимого уровня обобщения на примере раздела программы курса физики 10-го класса «Уравнение состояния идеального газа» (предыдущий раздел – «Введение в термодинамику»). Уравнение состояния идеального газаОсновные тезисы раздела
Краткий конспект лекций 1. Состояние системы –
совокупность параметров, которые её
характеризуют. Состояние газа определяют 4
параметра: р, V, T, Единственная ТС, которая подробно рассматривается в курсе физики средней школы – идеальный газ (ИГ). Уравнение, которое связывает термодинамические параметры ИГ – уравнение газового термометра! Итак: уравнение газового термометра – уравнение
состояния ИГ – получено эмпирически. (Вопрос
учащимся: как получено?) В учебнике это
уравнение записано «в строку»:
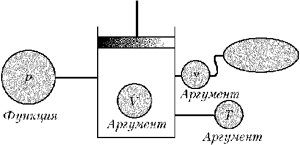
4. Алгебраический аспект проблемы С алгебраической точки зрения уравнение состояния ИГ можно рассматривать как задание функции многих (а именно трёх) переменных. Напоминаю: функция одной переменной – правило, по которому каждому элементу одного множества (множества значений аргумента) ставится в соответствие элемент другого множества (множества значений функции). Предлагаю учащимся самостоятельно сформулировать определение функции многих переменных. Представление уравнения состояния ИГ как задание функции многих переменных означает, например, следующее: давление в сосуде под поршнем (функция) изменяется при изменении количества вещества, температуры и объёма (аргументы). 5. Геометрический аспект проблемы Геометрическая интерпретация зависимости (график функции) – эффективное средство решения многих задач. Графическое представление (график) функции одной переменной величины – линия на плоскости (декартовой). Графическое представление функции двух переменных – множество точек пространства. (Речь идёт о пространстве параметров: оси декартовой системы координат являются шкалами соответствующих величин.) Графическое представление функции многих переменных – множество точек многомерного пространства параметров. Будучи не в состоянии представить себе пространство размерностью больше трёх измерений, человек может тем не менее оперировать геометрическими понятиями и в этом случае.
В ряде реальных процессов количество вещества ИГ не изменяется. Уравнение состояния ИГ задаёт в этом случае функцию двух переменных величин. Рассмотрим три взаимно
перпендикулярные шкалы (р, V, T),
совпадающие с рёбрами классной комнаты. Каждая
точка комнаты – состояние газа. Изменение
состояния газа – переход из одной точки комнаты
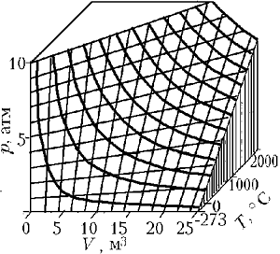
в другую. Вопрос учащимся: что можно сказать о множестве точек пространства параметров, отвечающих заданному количеству молей ИГ? (Ответ: поверхность в р, V, T-пространстве.) Демонстрируется картина этой поверхности. Каждая точка этой поверхности определяет возможное состояние газа. Переход из одного состояния в другое возможен лишь вдоль представленной поверхности. Другие точки пространства параметров представляют состояния, в которых газ находиться не может.
Геометрический смысл изопроцессов – сечения поверхности состояния плоскостями, параллельными координатным плоскостям. 6. Классификация графических задач
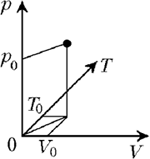
7. О чём спорят в парламенте Повторяем: состояние системы, состоящей из большого количества элементов, – совокупность параметров, которые описывают эту систему как целое. Уравнение состояния определяет связь между этими параметрами.Геометрический смысл уравнения состояния – поверхность в пространстве параметров. Категориями состояние–поверхность мыслят математик, физик, химик, социолог, экономист. Пространство, о котором идёт речь в каждом конкретном случае, определяется теми параметрами, которыми оперирует соответствующий специалист. В геометрических терминах легче разобраться, чем в перипетиях политических дискуссий. Состояние государства определяется совокупностью социально-экономических показателей (параметров). Геометрический смысл этого состояния – точка в пространстве параметров. Показатели некоторым образом связаны друг с другом. Геометрический смысл этой связи – поверхность в пространстве параметров. Разные политические силы могут иметь разные представления:
Дискуссия в парламенте между «условно либералами» и «условно социалистами» может сводиться к следующему. Представим себе, что обе партии одинаково представляют себе связь между параметрами, которые характеризуют состояния государства. Это значит, что у них нет разногласий по поводу вида поверхности в пространстве параметров. Представим себе также, что нет разногласий и по поводу цели, т.е. точки поверхности, к которой следует двигаться. Консенсус, однако, не достигнут в отношении путей следования к цели, т.е. линии, по которой следует двигаться от точки, отвечающей настоящему положению, к точке «процветания». «Либералы» полагают, что следует двигаться по линии, ведущей к цели за кратчайшее время, а «социалисты» предлагают двигаться по «длинному» пути, но с минимальными потерями для населения. Можно представить также спор между «либералами» и «коммунистами». «Коммунисты» утверждают, что они видят кратчайшую дорогу к цели и предлагают двигаться именно так. «Либералы» уверяют, что такое движение не представляется возможным: указанная дорога, действительно, кратчайший путь к цели, но она не лежит на поверхности, выражающей связь между параметрами, и, следовательно, не отвечает возможным состояниям общества. «Коммунисты», разумеется, не согласны. Их мнение таково: «либералы» неправильно представляют себе поверхность в пространстве параметров. Комментарий. Представленный «краткий конспект» – попытка синтеза знаний. Исходная тема лекции – повод проследить взаимосвязь существенных положений различных дисциплин. Намеченная логическая линия легко продолжается, охватывая всё новые разделы различных курсов. Естественным продолжением, к примеру, представляется рассмотрение энергетического подхода при выяснении средств, которые позволяют перевести ТС из одного состояния в другое. На подобных путях видится мне решение той задачи, которая формулировалась авторами цитированных работ – создание непредметного ядра образования. |