Л.И.ВАСИЛЕВСКАЯ, К.А.КОХАНОВ, М.В.ГЫРДЫМОВ,
ЦДООШ, г. Киров
center@extedu.kirov.ru

Кировская летняя многопредметная школа

Центр активного интеллектуального отдыха учащихся и педагогов

Кировская ежегодная летняя многопредметная школа (ЛМШ) основана в 1985 г. Игорем Соломоновичем Рубановым (завуч Центра дополнительного образования одарённых школьников, ЦДООШ). Она задумывалась как летний лагерь, где отдых сочетается с интенсивными занятиями. В 1993 г. к существующему с самого начала математическому отделению добавилось физическое (руководители Л.И.Василевская и К.А.Коханов) – для окончивших 8–10-й классы. Сейчас есть и биологический поток.

Благодаря подвижничеству и титаническому труду организаторов ЛМШ И.С.Рубанова и директора ЦДООШ Е.Н.Перминовой за 21 год лагерь превратился из областного в международный. В прошлом году в нём учились 120 школьников из Кировской области и более 270 из Ангарска, Барнаула, Белгорода, Березников, Вологды, Дзержинска, Екатеринбурга, Железногорска, Заречного, Ижевска, Иркутска, Йошкар-Олы, Казани, Калининграда, Калуги, Качканара, Кемерово, Киева (Украина), Красноярска, Кургана, Курчатова, Магнитогорска, Москвы, Мурманска, Набережных Челнов, Нижнекамска, Нижнего Новгорода, Нижнего Тагила, Озёрска, Омска, Оренбурга, Перми, Раменского, Самары, Саратова, Сарова, Северодвинска, Сент-Люса (Франция), Снежинска, Сыктывкара, Таллина (Эстония), Тобольска, Троицка, Ульяновска, Фрязино, Харькова (Украина), Чайковского, Якутска, в их числе – около трети участников заключительных этапов Всероссийской физической олимпиады 2004 и 2005 гг.

Почти ежегодно физики ЛМШ достойно представляют Россию на Международной физической олимпиаде: Васильев Д. (1996), Панов Е. (1999), Вавилов В. (2000), Нургалиев Д. (2001), Королёв К. (2001), Николаенко С. (2001) – Украина, учился в ЛМШ 1999 г., Мишутин И. (2003), Глазырин С. (2004), Ахунзянов Р. (2005).

Сейчас в ЛМШ преподают и бывшие её ученики (ныне студенты, аспиранты и уже кандидаты наук, выпускники МГУ, Физтеха, СПбГУ и других ведущих вузов страны), и лучшие школьные и вузовские учителя г. Кирова. Почти каждый новый преподаватель проходит предварительную стажировку в течение одной смены, что позволяет отобрать наиболее талантливых. Практически все используют авторские программы. Накоплен большой массив информации. С некоторыми материалами можно ознакомиться на сайте www.kirov.ru~/center.

Учащихся в летнюю школу набирают по конкурсу (до 6–7 человек на место). Конкурсные задания, включающие 10 нестандартных задач, рассылаются в апреле во все школы области и лично всем участникам районных и городских олимпиад и турниров. Вне конкурса принимаются получившие персональные приглашения по итогам учёбы в ЛМШ в предыдущем году, а также призёры Кировской областной олимпиады и победители окружного и заключительного этапов Всероссийской. Как правило, мы заранее знаем основной контингент предстоящей летней школы, т.к. работаем со школьниками в течение года в физических кружках и на факультативах, встречаемся с ними на олимпиадах и турнирах, в заочной физической школе при ЦДООШ.

Последние 9 лет лагерь организуется на базе дома отдыха «Вишкиль» Кировской области, в 150 км от областного центра, в живописном сосновом лесу на берегу Вятки, обычно в июле. Продолжительность смены 23–25 дней. Ежедневно с 9 до 13 ч проводятся занятия, а во второй половине дня – физические бои, консультации, кружки, лекции и факультативы. В каждой учебной группе не более 15 человек. на занятиях половина времени посвящена решению теоретических олимпиадных задач, а половина – экспериментальным заданиям олимпиадного уровня. Темы большинства занятий соответствуют школьной программе, но наряду с этим изучаются, например, динамика вращательного движения (9-й класс), термодинамика конденсированных систем (10-й класс) и т.п. Экспериментальные задачи выполняются на специальном учебном оборудовании (около 60 работ практически по всем разделам школьного курса физики).

Для оптимального использования предоставляемых помещений и оборудования очерёдность теоретических и экспериментальных занятий в разных классах неодинакова – в 8-м и 9-м классах в первую половину смены проходят занятия, связанные с изучением теории и решением задач, а во вторую – занятия, связанные с выполнением экспериментальных заданий, в 10-м классе – наоборот.

Тематика факультативных занятий зависит от интересов преподавателей. Особой популярностью пользуются факультативы «Занимательная физика», «Математика для физиков», «Физика элементарных частиц». Популярны также индивидуальные консультации, в ходе которых ученики либо получают разъяснения по наиболее трудным задачам и теоретическим вопросам, либо сдают решения выполненных во внеучебное время заданий. В процессе учебы вычисляется рейтинг учащихся, желающие повысить его сдают зачёт. Отличники получают персональное приглашение на следующий год.

По нашему мнению, задача летней школы состоит не только в том, чтобы углубить и расширить научные знания, развить творческие способности, но и, самое главное, дать возможность почувствовать каждому школьнику сладость (а иногда и горечь) научного поиска, создать благоприятные условия для интеллектуального общения с талантливыми сверстниками и педагогами, самоутвердиться как личность. Погружение в атмосферу любимой науки на целый месяц, да ещё летом, невозможно без всеобщей увлечённости, без ежедневных, пусть небольших, успехов.

В Кировской ЛМШ создалась неповторимая обстановка интеллектуального общения. Регулярные математические, физические и биологические бои привлекают школьников всех потоков. На них можно поспорить по задачам, не только требующих знаний, но и позволяющих проявить смекалку и творческую инициативу в соответствии с духом олимпиадного движения.

Несмотря на постоянные учебные занятия, досуг оказывается разнообразным. В течение всей смены продолжаются спартакиада (лёгкая атлетика, футбол, волейбол, настольный теннис, бадминтон, плавание), работают клубы по интересам – английский клуб и литературная гостиная, музыкальный и фото- клубы, кружки макраме, микологии, лингвистики. По вечерам – концерты самодеятельности, конкурсы («Мисс и мистер ЛМШ», «Устами младенца», «Что? Где? Когда?»), где школьники успешно сражаются со студентами и преподавателями. Всегда весело проходят общие праздники посвящения в ЛМШата, «День Эратосфена», «День Нептуна», вечера самодеятельной песни, дискотеки – всего не перечислить. И при этом учащиеся сами делают выбор, как провести своё свободное время. Как отмечают многие ученики, летней школе присущ «сумасшедший» ритм жизни, и поэтому после каждой ЛМШ остаётся множество впечатлений и воспоминаний на долгие месяцы, появляется громадное количество идей, которые хочется реализовать сразу после школы. Летняя школа позволяет сориентироваться, понять, к чему нужно стремиться на протяжении учебного года, чтобы уже в следующей школе показать уровень знаний и проявить свою компетентность.

И здесь, под слоем эмоций и впечатлений, скрывается самое главное – стремление учащихся к познанию и определению путей самореализации.

Приводим несколько оригинальных и занимательных задач из практики ЛМШ.

1. Экспериментальная задача: определите толщину «подошвы» лапок комара.

Оборудование: любое доступное.

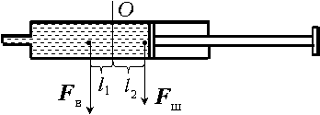
Решение, предложенное жюри: используйте явления дифракции. Если осветить ножку комара пучком от лазерной указки, то на удалённом экране можно получить дифракционную картину. Определив положения главных максимумов, легко рассчитать поперечные размеры лапок комара:

2. Цилиндрическая линза. Оцените оптическую силу бутыли-линзы с водой. В данном случае можно использовать формулу тонкой линзы.

Возможные рассуждения при оценке фокусного расстояния. Ученики могли измерить поперечные размеры бутыли, а также даваемое бутылью увеличение размеров глаз. Зная расстояние от бутыли до глаз и увеличение, можно определить фокусное расстояние и оптическую силу наполненной водой бутыли. Так, при увеличении вертикального размера глаза Г = 2,5 и расстоянии от глаза до оси бутыли f = 0,05 м оптическая сила бутыли

3. «Мёртвая» лужа. Определите плотность грязи в луже (предположительно очень глубокой), чтобы в ней не смогла бы утонуть девочка.

Указание к решению. Совершенно очевидно, что реальная лужа неглубокая. Но, если предположить, что глубина достаточная, условие плавания можно записать так: mg = F_A. Учитывая, что девочка погружена в лужу примерно на 1/7 часть своего объёма, и её плотность примерно равна плотности солёной воды (1030 кг/м³), можно определить плотность грязи в луже:

_rлужи = 7 ^.1030 кг/м³ 7200 кг/м³.

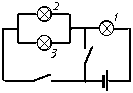
4. Лампочка Ильича. При подключении в сеть трёхламповой люстры с двумя выключателями была допущена ошибка. В результате этого при замыкании одного из выключателей все три лампы горели неполным накалом. При замыкании другого выключателя горела нормальным накалом только одна из ламп (две другие не горели), и тот же эффект давало замыкание обоих выключателей одновременно. При разомкнутых выключателях все три лампы не горели. Нарисуйте возможную схему выполненного монтажа, объясните наблюдаемые эффекты.

Решение. Возможная цепь показана на рисунке. Можно также собрать цепь, где лампы 2 и 3 соединены последовательно.

5. Девочка-дракон. Оцените мощность лёгких девочки, плюющейся водой. Экспозиция при фотографировании 1/320 с.

Возможные рассуждения. Найдём скорость v вылета жидкости изо рта девочки. Для этого рассмотрим самые удалённые от девочки капли. Пролетев по горизонтали приблизительно s = 60 см, они отклонились вниз примерно на h = 10 см. Учитывая, что капли изо рта вылетают практически горизонтально, получим и откуда

Если считать, что к моменту окончания фотографирования девочка выплюнула всю воду, то мощность можно оценить так:

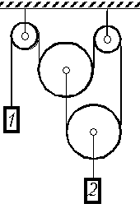
где

Тогда

6. Грузы, блоки… Определите связь ускорений грузов 1 (масса m₁) и 2 (масса m₂) в системе, показанной на рисунке. Блоки невесомы, нити нерастяжимы, трения в осях блоков нет.

Решение. Оба груза будут свободно падать, т.к. при данном расположении блоков сила натяжения равна нулю. Это следует из анализа поведения верхнего большого блока: при равенстве нулю его массы из второго закона Ньютона получается, что 0 = 2Т – Т, где Т – модуль силы натяжения нити, или Т = 0.

6. Сказка – ложь, да в ней намёк… Демонстратор держится за провод, подсоединённый к электроскопу, и подпрыгивает. При этом стрелка электроскопа отклоняется и возвращается назад после приземления. Объясните наблюдаемое явление.

Решение. В области соприкосновения подошв и пола имеются небольшая контактная разность потенциалов и заряды противоположных знаков. Эти заряды возникают из-за трения подошв ботинок об пол во время ходьбы. При увеличении зазора напряжение «конденсатора» возрастает, соответственно возрастает и заряд электроскопа. При приземлении исходная ситуация восстанавливается.

Ещё один вариант объяснения: систему человек–пол можно представить, как два параллельных конденсатора. Ёмкость первого многократно превышает ёмкость второго, и потому весь имеющийся заряд сконцентрирован на подошве. При уменьшении ёмкости конденсатора человек–пол (человек подпрыгивает) заряды в системе перераспределяются. При восстановлении начальной ситуации (человек приземляется) всё приходит в начальное состояние.

Экспериментальные задачи заключительной олимпиады 2005 г. Обратим внимание на то, что задачи выполняются не в лаборатории, а прямо на лесной поляне или на берегу реки. Ряд предложенных задач не имеют однозначного решения, но позволяют проверить, насколько ученик готов к применению полученных знаний на практике.

8-й класс

1. Определите размер и плотность песчинки.

Оборудование: любое количество песчинок и любое доступное оборудование (кроме штангенциркуля и микрометра).

Указание к решению. Для определения размера можно использовать известный метод рядов. Однако лучше всего насыпать песок в баллон шприца с водой, определить объём воды, вытесняемой песком, и рассчитать суммарный объём песка, а пересчитав песчинки, – средний объём одной. Массу песка можно определить так. Насыпать его в плавающий в воде цилиндрический стакан, по изменению уровня стакана в жидкости h определить добавочную силу Архимеда F_Арх, вычислить Далее понятно.

2. Определите массу шприца.

Оборудование: шприц, нитка, вода.

Возможное решение сводится к сравнению массы шприца с массой набранной в него воды. К баллону шприца привязывают нить, в шприц набирают воду (больше половины баллона). Шприц поднимают за нить, причём сдвигают её по баллону так, чтобы шприц принял горизонтальное положение.

Условие равновесия системы: , где F_ш – сила тяжести, действующая на шприц, F_в – сила тяжести, действующая на воду. Плечо силы F_в определяют по делениям шкалы шприца. Для определения l₂ находят положение центра тяжести пустого шприца при неизменном положении поршня. Для этого из шприца выливают воду, поршень отводят в прежнее положение (по делениям шкалы), нить сдвигают по шприцу до тех пор, пока шприц вновь не будет висеть горизонтально. Новое положение нити позволяет рассчитать плечо силы тяжести шприца l₂. В итоге

9-й класс

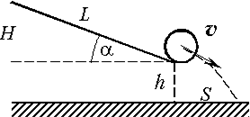
1. Исследуйте, как зависит характер движения сплошного цилиндра на наклонной плоскости от её наклона. Определите коэффициент трения скольжения.

Оборудование: банка консервов, стол (выносится на улицу), мерная лента.

Возможное решение. Измеряют длину стола L, высоту его над землёй h. По дальности полёта определяют скорость в конце плоскости при разных углах наклона: . При небольших углах наблюдается скатывание без проскальзывания, при этом

(1)

При проскальзывании причём

Можно показать (см. ниже), что проскальзывание начинается при и что при угле, большем ₀, значения _э не соответствуют ₁. Сопоставив таблицу значений скоростей, полученных экспериментально и вычисленных по формуле (1) для различных углов, нужно обнаружить существенное их расхождение при некотором угле и сделать вывод об изменении характера движения цилиндра.

Далее определяют коэффициент трения . Получают связь между ₀ и . При проскальзывании центр масс цилиндра движется с ускорением . Тангенциальное ускорение, с которым движутся точки цилиндра вокруг его центра,

При проскальзывании

а > a₁;

2. Оцените силу, с которой вы давите пальцем на поршень медицинского шприца с водой.

Оборудование: шприц без иглы, сосуд с водой, линейка.

10-й класс

1. Изучите, как зависит прогиб горизонтально закреплённой линейки от её длины и массы подвешиваемого груза.

Оборудование: линейка, грузы по 100 г, нитка, миллиметровая бумага, подручные материалы.

Решение. Снимают и исследуют зависимости. Получают, что отклонение x свободного конца линейки от горизонтали пропорционально массе m подвешиваемого груза при фиксированной длине линейки и третьей степени длины свободного участка линейки L³ при одной и той же массе груза, т.е. x ~ mL³.

2. Имеется цилиндрическая заготовка (из оргстекла). Определите наибольшее количество параметров этого материала.