В.Б.ДРОЗДОВ,г. Рязань Человек на водеБольшинство, очевидно, умеет плавать. Перемещение в воде можно рассматривать как своего рода эксперимент, так что представляет интерес теоретически разобрать три вопроса. Первый: легко ли держаться на воде? или, конкретнее: какую наименьшую мощность должен развить человек, чтобы не утонуть в спокойной воде? Сначала возьмём из
справочников значения необходимых величин:
плотность человека 1030 кг/м3 Ясно, что расчёт будет носить оценочный характер ввиду наличия ряда факторов, которые невозможно точно учесть: техника, скорость, амплитуда движений пловца, геометрическая форма его тела, объём лёгких и степень заполнения их воздухом, объём части головы, находящейся над водой. Кроме того, более детальные вычисления были бы неимоверно сложны, если вообще возможны. Итак, пусть человек, лёжа в
воде на спине (а так легче всего), немного двигает
ногами и руками, не погружаясь на дно. При этом он
очень медленно плывёт, допустим, со скоростью
0,1 м/с. Как увидим ниже, энергозатратами на
такое «плавание» можно пренебречь по сравнению с
работой, совершаемой для удержания на воде.
Считаем пловца в первом приближении
прямоугольным параллелепипедом высотой H,
шириной 2a и толщиной a. Записав объём
человека двояко (V = Если пловец перестанет
«шевелиться», он начнёт погружаться в воду. Так
как плотность человека лишь немного больше
плотности воды, то считаем скорость погружения
В формуле (1) неизвестна только
скорость погружения
где S – площадь лобового сечения тела, C – безразмерный коэффициент, зависящий от его геометрической формы. Для диска, например, C = 1,1, поэтому разумно положить для человека C = 1. К формуле (2) легко прийти из
соображений размерности. Существует лишь
единственная комбинация из величин
откуда
Из формул (1) и (3) после технических упрощений получаем интересующий нас результат:
Мощность в формуле (4) выражена
через естественные характеристики человека:
массу и рост, а также через его плотность и
плотность воды. Она применима только при Интересно, что даст формула (4)
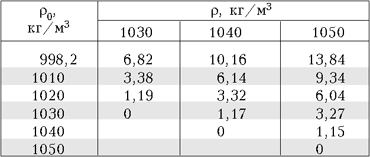
для воздуха ( Таблица 1. Мощность (Вт),
которую нужно развить человеку плотностью
Теория согласуется с опытом на качественном уровне, хотя формула (4) и неприменима для воздуха. Второй вопрос: легко ли
плыть, преодолевая сопротивление воды? Другими
словами, какую мощность N1 должен
развить человек, чтобы плыть со скоростью Ясно, что искомая мощность N1 = N
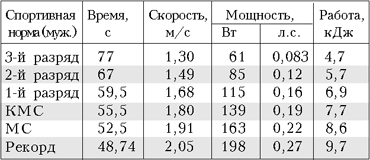
+ Fc N1 = N + Легко подсчитать, что N На основании формулы (5), в которой считаем N = 13,84 Вт, составлена табл. 2 для заплыва мужчин на 100 м вольным стилем. Из неё видим, как резко увеличивается мощность со скоростью. Третий вопрос: при какой глубине водоёма человеку безопасно прыгать в воду? Пусть рост человека H, а высота берега l. Отметим, что высота l даже в спортивных прыжках не превосходит 10 м, так что учитывать сопротивление воздуха нет необходимости. Также пренебрегаем незначительной горизонтальной составляющей скорости прыгуна по сравнению с вертикальной составляющей при вхождении в воду. Ввиду того, что плотность человека незначительно превышает плотность воды, не учитываем уменьшение потенциальной энергии системы вода–человек в процессе погружения человека на дно и считаем, что потенциальная энергия человека mgl полностью расходуется на работу против силы сопротивления воды. При этом скорость человека у дна обратится в нуль или станет безопасно малой. Пусть прыгун входит в воду вертикально, тогда сила сопротивления воды будет наименьшей, а риск удариться о дно – наибольшим. Таблица 2. Мощность, которую требуется развить спортсмену для того, чтобы плыть с указанной скоростью
Квадрат скорости вхождения в
воду зh ~ Полагая опять C = 1,
получим окончательно h ~ 3,5 м. (В
расчётах не учитывается вязкость воды, ибо даже
при скорости пловца 0,1 м/с число Рейнольдса Интересно, что в бассейнах для спортивных соревнований самые глубокие прыжковые ямы – восьмиметровые, а наибольшая глубина в обычном бассейне – 4 м. Это хорошо согласуется с нашей грубой оценкой. Ясно также, что столь глубокие ямы предназначены для прыжков с достаточно большой высоты, т.к. h всё же зависит от l. |
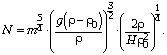 (4)
(4)