Проф. А.Б.ХМЕЛИНИН, С.Е.МУРАВЬЁВ,
МИФИ, г. Москва
Вступительные экзамены по физике-2005
Московский
инженерно-физический институт (МИФИ) – один из
старейших вузов страны, основанный в 1942 г. В его
становлении принимали участие крупнейшие
советские физики и математики: Я.Б.Зельдович,
И.В.Курчатов, М.А.Леонтович, Н.Н.Семёнов,
И.Е.Тамм, А.Н.Тихонов и др. МИФИ был создан
для подготовки инженеров-физиков, способных
решать актуальные проблемы современной науки и
новейших наукоёмких отраслей промышленности
(главным образом ядерной). Основой обучения таких
специалистов явилось сочетание
фундаментального университетского образования
с глубокой инженерной подготовкой. За годы
работы институт выпустил десятки тысяч
высококвалифицированных специалистов, в их
числе – лауреаты Нобелевской, Ленинской и
Государственной премий, руководители
научно-исследовательских институтов,
министерств, крупных промышленных предприятий.
В настоящее время МИФИ готовит
специалистов для традиционно важных отраслей
науки и техники, а также для новых, перспективных
направлений – биофизики, медицинской физики и
техники, экологии, компьютерных технологий и
информационной безопасности. В последние годы
начата подготовка специалистов в области
экономики, менеджмента, международного
научно-технологического сотрудничества,
бухгалтерского учёта, аудита, юриспруденции. В
состав МИФИ входят шесть факультетов дневного
обучения (экспериментальной и теоретической
физики, физики и экономики высоких технологий,
автоматики и электроники, кибернетики,
информационной безопасности, гуманитарный),
вечерний факультет (очно-заочное обучение), а
также высшая школа физиков и высший физический
колледж. Имеется штат стажёров-исследователей,
аспирантура и докторантура, по ряду
специальностей открыты магистратура и
бакалавриат. Есть военная кафедра. Иногородним
студентам предоставляется общежитие. Телефон
приёмной комиссии 324-8417.
Абитуриенты, поступающие на
физико-математические факультеты МИФИ, сдают два
конкурсных вступительных экзамена (математика и
физика) и зачёт по русскому языку (изложение).
Экзамен по физике – письменный, с устной защитой
результатов работы.
ВАРИАНТ ЗАДАНИЯ
1. Механическое движение.
Относительность движения. Система отсчёта.
Траектория. Путь и перемещение.
2. Постройте графики
изотермического, адиабатического,
изохорического и изобарического процессов,
проходящих с одноатомным идеальным газом, в
координатных осях Q, A, где Q – количество
теплоты, сообщённое газу, A – работа,
совершённая газом.
3. Линза с фокусным расстоянием
F = 5 см создаёт прямое изображение предмета,
перпендикулярного главной оптической оси, с
увеличением Г = 5. Найдите расстояние между
предметом и его изображением. 
4. N металлических пластин (N
– чётное число) площадью S расположены в
вакууме параллельно друг другу на одинаковых
расстояниях d и соединены так, как показано на
рисунке. Найдите ёмкость между точками A и B.
Считайте, что размеры пластин много больше
расстояний между всеми пластинами.
Решения
1. Механическое движение тела
– это его перемещение с течением времени
относительно другого тела, условно принимаемого
за неподвижное. Из определения движения следует,
что движение одного и того же тела будет
существенно различным в зависимости от того,
какое тело принимается за неподвижное. Например,
тело, падающее из состояния покоя в равномерно
движущемся поезде, перемещается прямолинейно по
отношению к телам, расположенным в поезде, и
движется криволинейно по отношению к телам,
расположенным на поверхности Земли.
Поскольку движение тел
происходит в пространстве и времени, для
количественного описания движения необходимо
измерять расстояния между телами и интервалы
времени. Неподвижное тело и связанная с ним
система координат, в которой выбраны масштаб для
измерения расстояний и часы для измерения
интервалов времени, называется системой
отсчёта. Можно построить множество различных
систем отсчёта. Выбор системы отсчёта для
описания того или иного движения определяется
соображениями удобства.
Траекторией движения тела
называется линия, вдоль которой движется тело.
Траектории могут быть прямыми (в этом случае
говорят о прямолинейном движении) или кривыми
(криволинейное движение).
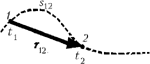 Пусть в некоторый момент
времени t1 тело находилось в точке 1,
в некоторый последующий момент времени t2
– в точке 2. Длина участка траектории s12
между точками 1 и 2 называется путём,
пройденным телом за интервал времени t2
– t1.
Пусть в некоторый момент
времени t1 тело находилось в точке 1,
в некоторый последующий момент времени t2
– в точке 2. Длина участка траектории s12
между точками 1 и 2 называется путём,
пройденным телом за интервал времени t2
– t1.
Перемещением тела за интервал
времени t2 – t1 называется
вектор r12, начало которого
находится в точке 1, конец – в точке 2. Для
любого движения тела справедливо соотношение s
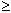 |r|,
причём равенство здесь имеет место только для
прямолинейного движения в одном направлении. Для
любого другого движения неравенство будет
строгим.
|r|,
причём равенство здесь имеет место только для
прямолинейного движения в одном направлении. Для
любого другого движения неравенство будет
строгим.
2. Согласно первому закону
термодинамики, количество теплоты Q,
сообщённое газу, изменение его внутренней
энергии 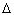 U
и работа газа A связаны друг с другом
следующим образом: Q =
U
и работа газа A связаны друг с другом
следующим образом: Q = 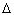 U + A. Получим отсюда связь
между U и A для перечисленных процессов.
U + A. Получим отсюда связь
между U и A для перечисленных процессов.
Изотермический процесс.
Поскольку внутренняя энергия одноатомного
идеального газа определяется соотношением U = (3/2)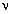 RT, где
RT, где 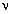 – число молей газа, R
– универсальная газовая постоянная, T –
абсолютная температура газа, то изменение
внутренней энергии газа в изотермическом
процессе равно нулю:
– число молей газа, R
– универсальная газовая постоянная, T –
абсолютная температура газа, то изменение
внутренней энергии газа в изотермическом
процессе равно нулю: 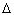 U = 0, т.е. количество теплоты,
сообщённое идеальному газу в изотермическом
процессе, равно совершённой им работе: Q = A. График
зависимости Q (A) представляет собой
прямую линию, проходящую через начало координат
и лежащую в первой и третьей четвертях
координатной плоскости. Если на осях Q и A
выбран одинаковый масштаб, то эта прямая
расположена под углом 45° к координатным осям
(график 1 на рисунке).
U = 0, т.е. количество теплоты,
сообщённое идеальному газу в изотермическом
процессе, равно совершённой им работе: Q = A. График
зависимости Q (A) представляет собой
прямую линию, проходящую через начало координат
и лежащую в первой и третьей четвертях
координатной плоскости. Если на осях Q и A
выбран одинаковый масштаб, то эта прямая
расположена под углом 45° к координатным осям
(график 1 на рисунке).
Адиабатический процесс: газ
не обменивается теплом с окружающими телами,
поэтому Q = 0 (график 2). 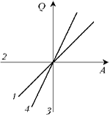
Изохорический процесс:
объём газа не изменяется, поэтому газ не
совершает работу: А = 0 (график 3).
Изобарический процесс: газ
совершает работу А = р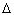 V, где p – давление газа,
V, где p – давление газа, 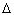 V –
изменение его объёма в этом процессе. Поэтому из
закона Клапейрона–Менделеева имеем: А =
V –
изменение его объёма в этом процессе. Поэтому из
закона Клапейрона–Менделеева имеем: А = 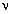 R
R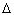 T.
T.
Поскольку для одноатомного
идеального газа U = (3/2)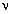 R
R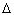 T,
то:
T,
то:
Q = (3/2)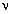 R
R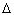 T +
T + 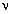 R
R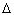 T = (5/2)
T = (5/2)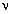 R
R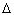 T = (5/2)A.
T = (5/2)A.
График зависимости Q от A
для изобарического процесса отмечен на рисунке
цифрой 4. 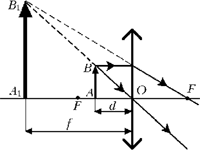
3. Поскольку изображение
прямое и увеличенное (Г > 1), то линза –
собирающая, изображение предмета мнимое
(изображение предмета в рассеивающей линзе –
уменьшенное, действительное изображение
предмета в собирающей линзе – перевёрнутое).
Поэтому расстояние от предмета до линзы меньше
фокусного расстояния линзы (на рисунке предмет и
его изображение обозначены как AB и A1B1
соответственно). Поэтому формула тонкой линзы
для рассматриваемого случая имеет вид: 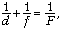 где d –
расстояние от предмета до линзы, причём 0 < d
< F, |f| – расстояние от изображения до
линзы (f < 0), F > 0 – фокусное расстояние
линзы. Получаем
где d –
расстояние от предмета до линзы, причём 0 < d
< F, |f| – расстояние от изображения до
линзы (f < 0), F > 0 – фокусное расстояние
линзы. Получаем 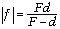 .
.
Увеличение предмета
определяется как отношение размера изображения
к размеру предмета: 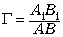 . Из подобия треугольников ABO и A1B1O
(O – оптический центр линзы) находим:
. Из подобия треугольников ABO и A1B1O
(O – оптический центр линзы) находим: 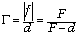 .
.
Находим расстояние между
предметом и линзой: 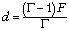 , а через него – расстояние от
изображения до линзы
, а через него – расстояние от
изображения до линзы 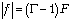 и, наконец, расстояние
и, наконец, расстояние 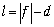 между предметом и его
изображением в линзе:
между предметом и его
изображением в линзе: 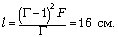
4. Чтобы найти ёмкость данной
системы проводников, сообщим проводнику,
связанному с точкой A, некоторый заряд Q,
проводнику, связанному с точкой B, – заряд –Q,
найдём разность потенциалов 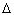
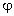 между проводниками A и B, вычислим
отношение Q/
между проводниками A и B, вычислим
отношение Q/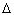
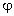 ,
которое, по определению, и есть ёмкость системы
двух проводников.
,
которое, по определению, и есть ёмкость системы
двух проводников.
Сначала определим, как
распределится сообщённый проводникам заряд по
пластинам. Поскольку все пластины, соединённые с
точкой А, представляют собой один проводник,
а все пластины, соединённые с точкой В, –
второй, то разность потенциалов между любой
пластиной, связанной с точкой А, и любой
пластиной, связанной с точкой В, будет
одинаковой. Поэтому сообщённые заряды
распределятся по пластинам так, что
напряжённость суммарного электрического поля
между каждой парой пластин будет одинаковой по
величине, а направления вектора напряжённости в
зазорах между двумя соседними парами пластин
будут взаимно противоположными.
Для нахождения зарядов
пластин заметим, что, согласно принципу
суперпозиции, электрическое поле между каждой
парой пластин создаётся зарядами всех пластин.
Однако разность напряжённостей суммарного
электрического поля с одной и с другой стороны от
каждой пластины определяется поверхностной
плотностью зарядов только этой пластины и не
зависит от зарядов других пластин.
Действительно, согласно принципу суперпозиции,
напряжённости суммарного поля с двух сторон от
одной из пластин E1 и E2
определяются соотношениями:
E1 = Eпл1 +
E; E2 = Eпл2 + E,
где Eпл1 и Eпл2
– напряжённости поля, созданного зарядами этой
пластины с одной и с другой стороны от неё, E
– напряжённость поля, созданного зарядами
других пластин. Отсюда следует, что разность Eпл1
– Eпл2 определяется только зарядами
рассматриваемой пластины и не содержит поле
зарядов других пластин. Учитывая, что |Eпл1|
= |Eпл2| = 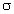 /(2
/(2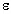 0),
где
0),
где 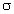 –
поверхностная плотность зарядов
рассматриваемой пластины,
–
поверхностная плотность зарядов
рассматриваемой пластины, 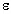 0 – электрическая
постоянная, а направления векторов Eпл1
и Eпл2 взаимно противоположны,
получим: |Eпл1– Eпл2| =
0 – электрическая
постоянная, а направления векторов Eпл1
и Eпл2 взаимно противоположны,
получим: |Eпл1– Eпл2| = 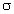 /
/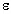 0.
0.
Отсюда следует, что изменение
напряжённости суммарного поля при «переходе»
через каждую пластину равно отношению
поверхностной плотности заряда этой пластины к
электрической постоянной и не зависит от того,
как заряжены другие пластины.
Теперь можно найти заряды
пластин. Поскольку напряжённости поля между
двумя соседними парами пластин одинаковы по
величине и противоположны по направлению, а поле
вне пластин равно нулю (последнее следует из
того, что суммарный заряд всех пластин равен
нулю), то изменение вектора E при
«переходе» через каждую внутреннюю пластину
одинаково, а через крайние пластины – вдвое
меньше. Поэтому заряды всех внутренних пластин
одинаковы по величине, а заряды двух крайних –
вдвое меньше зарядов внутренних. Отсюда получаем
для зарядов пластин, соединённых с точкой А: 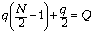 , где q – заряд
каждой внутренней пластины (заряды пластин,
соединённых с точкой B, противоположны по
знаку). Из последнего уравнения находим:
, где q – заряд
каждой внутренней пластины (заряды пластин,
соединённых с точкой B, противоположны по
знаку). Из последнего уравнения находим: 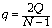 .
.
Отсюда можно найти
напряжённость электрического поля между любыми
соседними пластинами. Для этого рассмотрим
область между крайней и следующей пластинами.
Так как заряд крайней пластины равен q/2, где q
определяется написанной выше формулой, то
суммарный заряд всех остальных пластин равен –q/2.
Поэтому напряжённость электрического поля в
рассматриваемой области равна удвоенному полю,
создаваемому крайней пластиной:
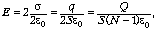
где 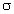 = (q/2)/S – поверхностная плотность
зарядов крайней пластины, S – площадь
пластин. Из последней формулы находим разность
потенциалов между крайней и соседней пластинами,
которая равна разности потенциалов между
точками А и В:
= (q/2)/S – поверхностная плотность
зарядов крайней пластины, S – площадь
пластин. Из последней формулы находим разность
потенциалов между крайней и соседней пластинами,
которая равна разности потенциалов между
точками А и В:
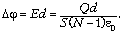
Подставляя эту разность потенциалов в
определение ёмкости, найдём ёмкость
рассматриваемой системы проводников: 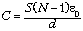 .
.
__________________________
Александр Борисович Хмелинин
– первый проректор, заведующий кафедрой общей
физики МИФИ, д.ф.-м.н., профессор.
Сергей Евгеньевич Муравьёв –
заместитель заведующего кафедрой теоретической
физики МИФИ, к.ф.-м.н., доцент.