А.Н.ДОЛГУШИН,
МОУ СОШ № 39, с. Ашитково, Воскресенский р-н,
Московская обл.
Решение блока задач методом
суммирования
Факультативный курс «Практикум
решения физических задач», 11-й класс
Динамика. Второй закон
Ньютона [1, 2]
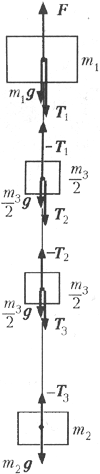
1. К грузу массой 7 кг
подвешен другой груз массой 5 кг. Какое натяжение
будут испытывать верхний конец и середина
каната, если всю систему поднимать вертикально
вверх с силой 240 Н, приложенной к большему
грузу? Масса каната 4 кг.
Указания к решению задачи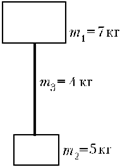
Динамика. Закон всемирного
тяготения*
2. Определите, с какой силой
однородное кольцо массой M и радиусом R
притягивает к себе шарик массой m,
расположенный на расстоянии h от центра
кольца на перпендикуляре к плоскости кольца,
проходящем через его центр. Размерами шарика
пренебречь.
Указания к решению задачи
Закон всемирного тяготения
справедлив только в отношении точечных тел.
Разбиваем массивное кольцо
на элементарные равномерно распределённые
ячейки, которые рассматриваем как материальные
точки массой Mi.
Притяжением между
элементарными ячейками кольца пренебрегаем.
Легко сообразить, что
результирующая сила Fрез будет
направлена от шарика к центру кольца и являться
суммой всех сил притяжения (гравитационных сил) Fгр i,
действующих со стороны элементарных масс Mi
на шарик. Задача сводится к определению силы
притяжения (гравитационной силы) Fгр i
между каждой i-й ячейкой и шариком.
Вклад в результирующую силу
со стороны каждой i-й ячейки: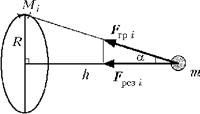
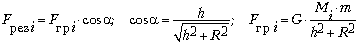 ,
,
где G – гравитационная
постоянная.
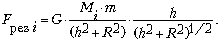
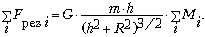
Поскольку G, m, R, h
являются величинами постоянными, их можно
вынести за знак суммирования. Сумма масс всех
элементарных ячеек есть масса кольца M:
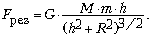
Электростатика. Закон
Кулона [1, 2]
3. Тонкое проволочное кольцо
радиусом R имеет электрический заряд q. В
центре кольца расположен одноимённый заряд Q  q.
Определите силу T, растягивающую кольцо.
q.
Определите силу T, растягивающую кольцо.
Указания к решению задачи
Закон Кулона прямо применять
нельзя. Равномерно заряженное кольцо разбиваем
на элементарные 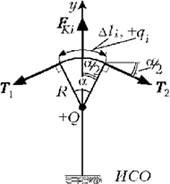 ячейки, которые можно
представить как точечные заряды.
ячейки, которые можно
представить как точечные заряды.
Сделаем рисунок для i-й
ячейки.
Всё кольцо растянуто
равномерно. Обе силы растяжения Т1
и T2 обусловлены
упругими силами в кольце.
Поскольку ячейка находится в
состоянии покоя, а заряд считаем расположенным в
центре кольца, записываем второй закон Ньютона
для i-й ячейки: FКi + T1
+ T2 = 0.
Находим проекции векторов
действующих сил на направление Y:
FКi = 2Tsin(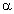 /2);
/2);
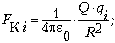
Синусы малых углов заменяем
самими углами в радианах: 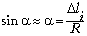 .
.
Суммируем вклады от всех
ячеек, учитывая, что сумма всех зарядов
элементарных ячеек есть q, а сумма всех длин
элементарных ячеек есть 2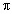 R:
R:
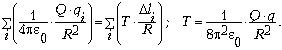
Электростатика. Напряжённость
– силовая характеристика электрического поля.
Потенциал – энергетическая характеристика
электрического поля [1]
4. По кольцу радиусом R
равномерно распределён заряд Q. Определите
напряжённость электрического поля и его
потенциал в центре кольца, а также в точке,
отстоящей на расстоянии h от центра кольца по
перпендикуляру к плоскости кольца.
Указания к решению задачи
Для определения
напряжённости электрического поля в некоторой
точке в неё необходимо поместить положительный
единичный заряд. В центре Е0 = 0.
Потенциал электрического
поля точечного заряда является скалярной
величиной: 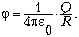
Решение аналогично решению
задачи 2.
На расстоянии h от центра
кольца:
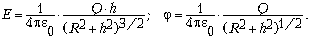
Магнитное поле. Сила Ампера в
комбинации с механическим напряжением [3]
5. По жёсткому кольцу из
медной проволоки течёт ток силой 5 А. Кольцо
находится в перпендикулярном к его плоскости
магнитном поле индукцией 0,5 Тл. Найдите
растягивающее механическое напряжение в
проволоке, если радиус кольца 5 см, а площадь
сечения проволоки 3 мм2. Магнитным
взаимодействием между различными участками
кольца можно пренебречь.
Указания к решению задачи
Механическим напряжением
называется физическая величина, равная
отношению модуля силы упругости, возникающей при
деформации, к площади сечения образца,
перпендикулярного вектору силы упругости: 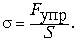
Сила упругости возникает в
результате действия магнитного поля на кольцо с
током. 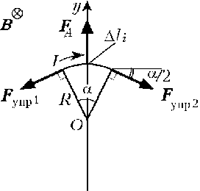
Равномерно разобьём кольцо
на элементарные ячейки. Сделаем рисунок, на
котором укажем направление всех сил, действующих
на одну ячейку. На все ячейки действуют
одинаковые по модулю силы упругости.
Для одной ячейки запишем
второй закон Ньютона в векторном виде, учитывая,
что она находится в равновесии: Y: FA + Fупр.1
+ Fупр.2 = 0.
Выбираем ИСО (ось Y) и
находим проекции действующих сил: FA = 2Fупрsin( /2).
/2).
Так как угол 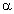 достаточно мал, то:
достаточно мал, то:
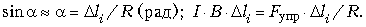
I • B = Fупр/R;
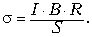
Литература
1. Славов А.В., Спивак В.С.,
Цуканов В.В. Сборник задач по физике: Под ред.
Славова А.В.: 6-е изд., испр. и доп. – М.: Изд-во МЭИ,
2004.
2. Дмитриев С.Н., Васюков
В.В., Струков Ю.А. Сборник задач для
поступающих в вузы: Физика: 5-е изд. – М.:
Демиург–Арт, 2002.
3. Гельфгат И.М., Генденштейн
Л.Е., Кирик Л.А. 1001 задача по физике (с
ответами, указаниями, решениями): 3-е изд., перераб.
– М.–Харьков: Илекса–Гимназия, 1997.
_________________________________________
*Задача придумана автором по
аналогии с задачей из сборника «Качественные
задачи» М.Е.Тульчинского: «По закону
всемирного тяготения все тела притягиваются
друг к другу под действием гравитационных сил.
Приведите пример, когда при сближении двух тел
сила притяжения между ними уменьшается». Она
схожа и с задачей из раздела «Электростатика.
Напряжённость – силовая характеристика
электрического поля». Аналогия между законом
Кулона и законом всемирного тяготения, а также
между электростатическим и гравитационным
полями проводится довольно часто.
Все векторы обозначены жирным. – Ред.