А.А.СКЛЯНКИН, А.В.ЗОТЕЕВ,
|
Последнее десятилетие химический факультет МГУ им. М.В.Ломоносова в перечень вступительных экзаменов наряду с химией неизменно включает такие ключевые для химиков дисциплины, как математика и физика. Вступительные экзамены по математике и химии всегда проводятся в письменной форме. Начиная с 2004 г. экзамен по физике также письменный – абитуриенту вручается билет с десятью заданиями. В первых двух заданиях требуется дать формулировку предложенного физического закона и (или) определение предложенной физической величины. Ответ должен был быть кратким, но полным, и показывать знание абитуриентом сущности закона, физического смысла величин и понятий. В заданиях 3–7 проверяется умение применять теоретический материал при выполнении несложных практических заданий, зачастую содержащих графическое представление различных характеристик физических процессов, в том числе построение оптических изображений. Последний блок заданий представляет собой задачи в классическом понимании этого слова с нарастающим уровнем сложности. Все задания полностью соответствуют программе* вступительных испытаний по физике для поступающих в МГУ. Практически ежегодно различные издательства предлагают читателям новую продукцию в виде пособий, задачников и справочников. Качественный уровень и стиль изложения материала этих пособий весьма разнообразен. Поступающим в МГУ следует иметь в виду, что, несмотря на ежегодное обязательное обновление наших заданий, их стиль, традиции и уровень трудности сохраняются. Приводим несколько вариантов экзаменационных билетов с решениями (кроме ответов на теоретические вопросы). |
Вариант 1
1. Сформулируйте первый закон термодинамики.
2. Дайте определение понятия сила постоянного тока.
3. Материальная точка движется по оси Х под действием одной силы F, направленной вдоль X. По графику зависимости величины силы от координаты этой материальной точки определите работу, совершаемую этой силой на первых L = 6 м пути.
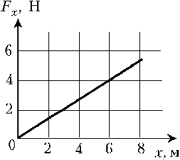
Решение
Работа силы при малом
перемещении материальной точки 
x равна A = Fx(x)x. Полная
работа на перемещении L равна сумме
элементарных работ А. Такое суммирование можно
выполнить графически – работа соответствует
площади фигуры под графиком зависимости Fx
от х:
Заметим, что подобным образом
вычисляется работа любой переменной силы.
Например, аналогичный расчёт работы против силы
упругости в области действия закона Гука
приводит к хорошо известному выражению для
потенциальной энергии деформированной пружины 
4. Во сколько раз изменится (увеличится или уменьшится) энергия взаимодействия двух одинаковых точечных зарядов в вакууме, если расстояние между ними уменьшить в 3 раза?
Решение
Энергия взаимодействия двух
точечных зарядов в вакууме равна 
Так как, по условию,
заряды одинаковы, то эта энергия положительна
(заряды отталкиваются) и увеличивается обратно
пропорционально расстоянию, т.е. в 3 раза.
5. Найдите работу, совершённую идеальным газом в процессе 1–2–3, представленном на рисунке. Значения p1, V1, p2, V2 и V3 определите по графику.
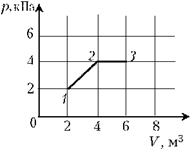
Решение
Работу, совершённую газом в произвольном процессе, можно найти, если известна зависимость давления газа от его объёма. В данной задаче эта зависимость представлена графически, и работу нетрудно рассчитать, определив площадь фигуры под соответствующим графиком**. В процессе 1–2 давление линейно нарастает, и работа равна
(Площадь трапеции под участком 1–2)
Затем в процессе 2–3 газ расширяется изобарно при давлении p2 = 4 кПа, поэтому
A2–3 = p2(V3 – V2) = 4 кПа • 2 м3 = 8 кДж.
Таким образом, полная работа газа в процессе 1–2–3 равна
Отметим, что газ расширяется и совершаемая им работа положительна.
6. Точка совершает
гармонические колебания вдоль оси X с
амплитудой А = 5 см и частотой 
= 5 Гц. Найдите величину скорости
точки в те моменты, когда её смещение от
положения равновесия равно x1 = 3 см.
Решение
Совместим начало отсчёта на оси Х с положением равновесия точки. Тогда закон движения точки (зависимость её координаты от времени), совершающей гармонические колебания вдоль оси X, может быть записан в виде:
x(t) = Asin(
t + 
0).
Здесь А – амплитуда, –
циклическая частота, а 0 – начальная фаза колебаний.
Моменты времени, когда смещение точки от
положения равновесия определяется координатой x1,
можно найти из равенства
x1 = Asin(t1 + 0).
Скорость точки может быть найдена как производная координаты по времени:
(1)
Чтобы найти скорость в интересующие нас моменты времени, достаточно выразить значение косинуса через синус того же аргумента:
(2)
затем подставить его в равенство (1) и учесть связь обычной и циклической частот колебаний:
= 2
.
Окончательно получаем модуль скорости точки:
7. Оцените угловую скорость
движения электрона в атоме водорода в модели
Бора, приняв радиус орбиты электрона r = 0,5 • 10–10
м. Заряд электрона e = –1,6 • 10–19 Кл, его
масса me = 9,1•10–31 кг.
Электрическая постоянная СИ 
0 
8,9 • 10–12
Ф/м.
Решение
В модели атома водорода Бора электрон движется по круговым орбитам вокруг ядра атома – протона. Это движение происходит под действием силы электрического притяжения, – которая может быть определена по закону Кулона
Именно эта сила сообщает электрону центростремительное ускорение, и на основании 2-го закона Ньютона можно записать:
meaцс = Fe.Из кинематики известна связь
центростремительного ускорения и угловой
скорости движения частицы по окружности: aцс
= 2r.
Решая совместно приведённые уравнения, находим
Заметим, что полученный результат позволяет не только оценить величины угловых скоростей движения электрона в атоме, но и даёт представление о частотах излучения атомов.
8. На наклонной плоскости с
углом наклона 
= 60° к горизонту лежит брусок массой m = 1 кг.
Наклонная плоскость помещена в лифт, движущийся
с ускорением a = 2 м/с2, направленным
вверх. Определите силу нормального давления
бруска на плоскость. Принять g = 10 м/с2.
Считать, что брусок не соскальзывает по
наклонной плоскости.
Решение
Укажем силы, действующие на брусок, – это сила тяжести mg, нормальная составляющая силы реакции опоры N и сила трения покоя Fтр. Выберем инерциальную систему отсчёта, связанную с Землёй. Оси системы координат расположим вдоль направления ускорения лифта (вертикально вверх) и перпендикулярно к нему.
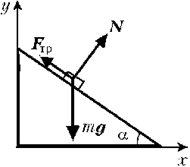
Тогда уравнения движения (второй закон Ньютона) бруска в проекциях на координатные оси будут выглядеть следующим образом:
В этих равенствах учтено, что, т.к. брусок не соскальзывает по наклонной плоскости (движется с ней совместно), его ускорение совпадает с ускорением наклонной плоскости.
Искомая сила нормального давления бруска на плоскость, по третьему закону Ньютона, равна по величине и противоположна по направлению нормальной составляющей силы реакции опоры N. Используя приведённые уравнения, получаем
N = m(g + a)cos = 6 Н.
9. Прямой проводник АА1 длиной l = 1 м и массой m = 100 г подвешен горизонтально на двух лёгких проводящих нитях в магнитном поле, направленном вертикально вверх. Какой силы I ток надо пропустить через проводник, чтобы нити порвались? Поле считать однородным, индукция В = 0,1 Тл. Каждая нить разрывается при натяжении Tmax = 1 Н. Принять g = 10 м/с2.
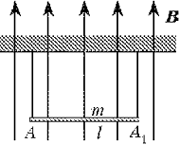
Решение
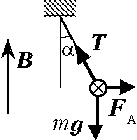На рисунке указаны силы,
действующие на проводник АА1. Символом 
показано
направление (от нас) протекающего в нём тока.
Запишем условия равновесия системы в проекциях
на горизонтальное и вертикальное направления:
Сила Ампера при этом равна
FА = IBl.
Здесь учтено, что вектор В перпендикулярен проводнику. При увеличении силы тока растёт угол отклонения, а также сила натяжения нитей подвеса Т. При максимальном натяжении нитей из второго равенства получаем
Если по проводнику пропустить больший ток, нити порвутся. Используя первое уравнение системы, приходим к окончательному результату:
______________________________
*Программа, а также список рекомендуемой учебной литературы публикуются в ежегодных справочниках и сборниках задач по физике для поступающих в МГУ.
**Сравните со случаем вычисления работы переменной силы в задании 3.