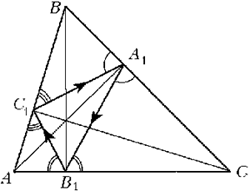
В.Б.ДРОЗДОВ, г. Рязань

Принцип Ферма и треугольник Шварца

Немецкий математик Герман Амандус Шварц (1843–1921) сформулировал и решил интересную и трудную задачу: «В остроугольный треугольник вписать треугольник наименьшего периметра». И хотя задача относится к элементарной геометрии, её решение более чем неэлементарное и длинное. А результат таков: вершинами искомого треугольника Шварца A₁B₁C₁ являются основания высот данного треугольника ABC.

Замечательно, что физика, приходя на помощь математике, даёт изящное и короткое решение этой задачи. Нам потребуется принцип известного французского математика Пьера Ферма (1601–1665): «Луч света всегда распространяется в пространстве между двумя точками по тому пути, вдоль которого время его прохождения меньше, чем вдоль любого из других путей, соединяющих эти точки» (ФЭС, М.: СЭ, 1983, с. 803). Понятно, что начальная и конечная точки в частном случае могут и совпадать.

Вначале отметим, что треугольники A₁BC₁ и ABC подобны как имеющие общий угол B и пропорциональные стороны, его заключающие:

Аналогично доказывается: AB₁C₁ ~ ABC и A₁B₁C ~ ABC.

Изобразим на рисунке равные углы равным числом дуг. Становится очевидным, что АА₁С₁ = АА₁В₁; ВВ₁С₁ = А₁В₁В; А₁С₁С = В₁С₁С. То есть высоты треугольника ABC являются биссектрисами треугольника A₁B₁C₁.

Теперь вообразим, что стороны треугольника АВС зеркальные. Поместим в точку А₁ точечный источник света и направим один из его лучей в точку В₁. Тогда в соответствии с законом отражения света этот луч попадёт в точку С₁ и далее вернётся в исходную точку А₁. Видим, что в силу принципа Ферма периметр треугольника A₁B₁C₁ будет наименьшим. Ибо, если взять хотя бы одну из точек A₁B₁C₁ в других местах на сторонах ВС, АС, АВ соответственно, то равенство хотя бы одной пары углов – АА₁С₁ и АА₁В₁; ВВ₁С₁ и А₁В₁В; А₁С₁С и В₁С₁С – нарушится. Следовательно, свет тогда не пойдёт по периметру треугольника А₁В₁С₁, а световой луч идёт в оптически однородной среде по кратчайшему пути.