МАРАФОН-2005

А.А.БУРОВ, Л.Е.СВИСТОВ,
школа № 179, г. Москва

Ниточки-верёвочки, или Принцип Ферма

Конец рабочего дня. Каждому хочется поскорее попасть домой. А что значит поскорее? Это значит, что из всех путей надо выбрать тот, который займёт меньше всего времени. Известно, что самые знатные определители наибыстрейших путей – ослы. Говорят, что в горных условиях они всегда выбирают наибыстрейший путь между начальной и конечной точками пути. Если, конечно, знают заранее, куда им предстоит идти. Спрашивается, кто (а может быть и что) способен найти самый быстрый путь между двумя точками? Великий Ферма подметил, что этим свойством обладает свет.

Такая формулировка принципа распространения света математически может быть записана так. Пусть среда оптически неоднородна, т.е. в каждой её точке имеется «своя» скорость света c = c (x, y, z). Тогда в силу соотношения ds² = dx² + + dz² принцип Ферма выражается соотношением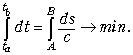

При этом сравнение осуществляется по путям, близким к пути, по которому свет приходит из точки A в точку B. Если наша среда оптически однородна, то
c = const, и свет будет двигаться по прямой. Если, конечно, ему не встретятся какие-нибудь препятствия.

Пример 1. Некто из точки A хочет сфотографировать объект, находящийся в точке B. Что может быть проще?! Наводишь фотоаппарат на B, и ответ готов. Но этот самый Некто вознамерился сфотографировать объект B с помощью плоского зеркала l, причём A и B расположены по одну сторону от этого зеркала. Спрашивается, куда ему надо целиться? (Эту задачу иной раз называют «задачей о ленивом ковбое»: наш ковбой должен проехать из пункта A в пункт B, напоив по дороге лошадь у реки, рис. 1, а, причём в силу своей лени выбрать кратчайший путь.)

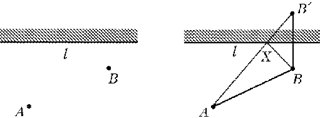
Рис. 1. а) Где ковбою надо напоить лошадь, чтобы побыстрее попасть из точки A в точку B? б) Конечно же, в точке X!

Ответ прост: Некто должен целиться в точку B' – образ точки B в зеркале l (рис. 1, б). Геометрическое объяснение этому факту, как известно, нетрудно получить с помощью неравенства треугольника. В самом деле, пусть X – некоторая точка на прямой l. Так как точки B и B' симметричны относительно этой прямой, то XB = XB'. Но тогда, согласно неравенству треугольника, суммарное расстояние AX + XB = AX + XB' минимально, если точки A, X и B' располагаются на одной прямой.

Ну а теперь зададимся вопросом: нельзя ли заменить «строгую геометрию» на что-нибудь такое, где доказательство, пусть на «физическом» уровне строгости, может быть «изготовлено» своими руками? Вспомним, что, растянув руками верёвочку, мы получим замечательную физическую интерпретацию того, что в геометрии понимают под прямой, точнее, отрезком прямой. Ну а теперь перекинем эту верёвочку через толстую проволоку с закреплёнными концами и вновь натянем её. Если трение между верёвочкой и проволокой мало, то мы сможем воочию убедиться в справедливости того, что «угол падения» верёвочки на проволоку равен (конечно, в точке «излома») «углу отражения» (рис. 2). Итак, изготовлен простой прибор для демонстрации экстремальных свойств света.

Рис. 2. Угол «падения» натянутой верёвочки на проволоку равен углу «отражения»

Замечание 1. Конечно, сила трения будет оказывать существенное влияние на равновесие рассматриваемой верёвочной системы. Задача об оценке такого влияния – достойный объект исследования не только для участников школьных физических кружков. А пока что экспериментаторы рекомендуют: прежде, чем демонстрировать результат, хорошенько потрясите конструкцию.

Пример 2. Теперь наш Некто хочет сфотографировать точку B из точки A с помощью пары параллельных зеркал l₁ и l₂ , причём, конечно, точки A и B находятся между этими зеркалами. Привычный ответ «с отражениями» уже не так прост – найдите-ка его! А в «верёвочном эксперименте» всё по-прежнему довольно просто: перекинем последовательно через прямые l₁ и l₂ верёвочку столько раз, сколько захотим, и натянем её так, чтобы концы оказались в A и B. Итак, ответ готов. Да и не просто ответ – целое множество ответов. Проще всего получается, конечно, в случае, когда верёвочка цепляет стороны по одному разу. В других случаях решения могут оказаться намного замысловатее.

Замечание 2. Эта же методика хороша и в том случае, когда зеркала l₁ и l₂ не параллельны. Перекидывай верёвочку поочередно через прямые l₁ и l₂, да натягивай так, чтобы концы оказались в A и B. Этакие катушки с нитками!

Пример 3. Тот же Некто из точки A с помощью пары непараллельных зеркал l₁ и l₂ хочет сфотографировать самого себя. В случае, если «дозволена» лишь парочка отражений, решение получится такое, как представлено на рис. 3, a. Геометрическое рассуждение, подтверждающее справедливость полученного результата, хорошо известно (см., например, Радемахер Г., Теплиц О. Числа и фигуры. Опыты математического мышления. – М.: Наука 1966, разделы 5, 6). Отразим точку A относительно прямых l₁ и l₂ (рис. 3, б). Получим точки A₁ и A₂. Соединим точки A₁ и A₂ отрезком. Тогда точки X₁ и X₂, в которых этот отрезок будет пересекать прямые l₁ и l₂, и будут в силу принципа Ферма точками отражения луча, идущего из A в A. На самом деле отрезок A₁A₂ короче любой ломаной A₁A₂, точки , которой принадлежат прямым l₁ и l₂ соответственно и не совпадают с X₁ и X₂.

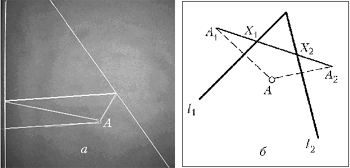
Рис. 3. Как сделать фотографию самого себя с двумя отражениями в зеркалах: а) построение на верёвочке; б) геометрическая интерпретация

Если же дозволено сделать, например, три отражения, то можно сфотографировать себя как в фас (рис. 4, а), так и «в затылок» (рис. 4, б).

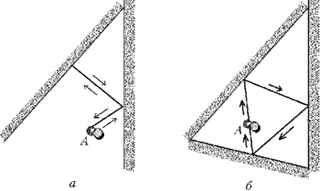
Рис. 4. Фотография самого себя с тремя отражениями: а) в фас; б) в затылок

Можно сделать фотографии и с большим числом отражений (рис. 5).

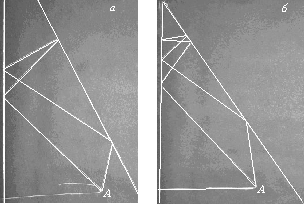
Рис. 5. Фотография самого себя: а) с четырьмя отражениями; б) с шестью отражениями

До сих пор мы предполагали, что наши зеркала – плоские. Именно это обстоятельство позволяло нам использовать в эксперименте прямые куски проволоки. Предположение о плоскостности зеркал, конечно, не является обязательным. Возьмём, например, сферическое зеркало, точнее, его сечение плоскостью, проходящей через центр сферы. Проволока в этом случае изогнута в виде окружности (рис. 6). Перекинем нашу верёвочку через получившуюся окружность, натянем её концы так, чтобы они оказались в точках A и B: луч света, идущий из A в B и отражающийся в нашем сферическом зеркале, найден.

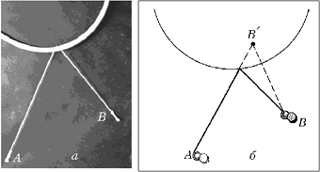
Рис. 6. «Отражение» луча в «сферическом зеркале» (а) и инверсия точки B (б), позволяющая понять, куда надо целиться

Любители геометрии тотчас сообразят, что для решения задачи геометрическими методами надо выполнить инверсию точки B относительно окружности, а затем соединить найденную таким образом точку B' с исходной точкой A (рис. 6, б). Точка пересечения X отрезка AB' с окружностью – это та точка, где должен отразиться свет, чтобы попасть в точку B.

Леонид Евгеньевич Свистов демонстрирует «игры с верёвочками» на Московском Дне физики (Марафон, 2005 г.)

Фото Е.Ольховской

Ну а теперь у нас полная свобода фантазии. Изображай прямыми кусками проволоки какие хочешь зеркала, протягивай, как хочешь, верёвочки, смотри, что получилось. Так, например, любителям стрелять из-за угла, вероятно, будет интересен вопрос о том, куда должен целиться Некто из A, чтобы попасть в Нечто из B, расположенное «за углом» зеркального коридора (рис. 7)?

Рис. 7. Стрельба из-за угла: а) куда надо целиться, чтобы из точки A попасть в точку B? б) одно из «экспериментальных» решений