Я имею знаковую форму на листе бумаги,
а объективное содержание этой знаковой формы
находится не здесь, на листе бумаги, а вне листа, в
другом месте.
Г.П.Щедровицкий*
(* Щедровицкий Г.П. Философия. Наука.
Методология. – М.: Школа культурной политики, 1997.)
Время, т.е. деятельность, за
последние двадцать лет существенно изменилось.
Интеллект всё смелее, хотя пока и косвенно,
становится стратегическим ресурсом страны
помимо его индивидуальной значимости для
развития. А значит, усвоение норм современного
мышления и мировоззрения должно быть обеспечено
содержательно и организационно. Следует
признать, что за последние годы понимание этих
качеств усложнилось, но в реальности
деятельность (по структуре и смыслам) школьников
фактически не изменилась. Никакое
дополнительное физическое содержание уже не
даст принципиального эффекта, если не будет
изменена сама деятельность. Эта установка пока
всё ещё рождается в муках.
Вот почему, по нашему мнению,
ключевым для продвижения в формирования
мышления школьников является изменение
отношения к физической задаче и процедурам,
связанным с её решением. Исторически эта
проблема уходит в послевоенные годы. Сейчас для
её разрешения есть основания: а) неплохая
теоретическая основа в виде психологии,
педагогики и методики физики; б)
демократизация учебного процесса; в)
востребованность умений решать задачи как в
узком смысле обучения (для сдачи ЕГЭ и других
экзаменов), так и в широком смысле (для реальной
жизни, для управления, производства, науки). Итак,
есть резон ставить вопрос о программе-проекте
совершенствования физического образования
через раскрытие потенциала школьных учебных
физических задач. Шаг вперёд отчасти позволяет
сделать элективный курс для 10–11-го классов
«Методы решения физических задач» [1]. Его цели
согласуются с общими задачами рассмотрения
вопросов методологии научного познания в
школьном курсе физики [1–4].
Методологическое основание
курса
Современное мышление и
деятельность как социальные по природе
образования включают в себя исторически
выработанные разные приёмы и способы, разные по
иерархии и содержанию знания. Практически все
они могут быть представлены в форме учебной
физической задачи. Могут и должны. Для целей
обучения физике это трудно переоценить. Школьная
учебная физическая задача, это, во-первых,
образование мышления и деятельности, во-вторых,
по функции, – это средство, инструмент
воспроизводства мышления и деятельности в
условиях обучения (усвоение нормы), в-третьих, это
объект изучения и исследования. Отсюда и
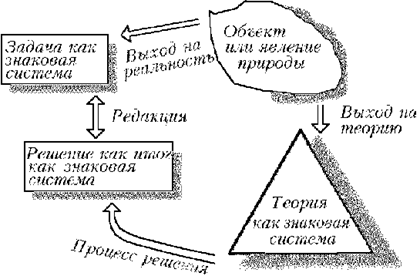
особенности отношения. Из приведённого ниже
рисунка чётко видны взаимные переходы «знак»
(знаковая система) – «объект (явление) природы»,
причём в ходе работы с задачей происходит
изменение знаковых систем (переформулировка
требования, изменение языка задания и др.). В этих
отношениях и переходах и реализуется
(выражается) мышление. Со знаками надо работать
на доске и в тетради, с объектами лучше
экспериментировать, но можно их и изображать,
понимая, что это обозначение реальности. Не
случайно опытные учителя подчеркивают значение
рисунка.
Учебные физические задачи в
большинстве случаев сформулированы в рамках
правил теории, фактически связаны и направлены
на освоение знаний этой теории. Это неплохо. Но
необходимо, что принципиально, ставить и решать
проблемы описания реальности. Именно тогда
вскрывается модельность наших представлений,
именно тогда формируются творческие умения
находить (строить) нужные методы решения,
понимать их ограниченность. Здесь громадный
ресурс интереса к физическому познанию.
Вспомним, как интересны экспериментальные
задачи! Общество физиков, методистов, учителей
должно быть едино в усилии – ни урока без
экспериментальной задачи! А это в том числе и
умение видеть задачи вокруг себя.
Учебная деятельность по
решению задач – это увлекательная (совместная,
напряжённая, эмоциональная, обязательно
результативная и т.д.) деятельность по достижению
победы над самим собой, над материалом задачи. Не
так важно, какие справочники вы используете, в
какой консультации нуждаетесь, как быстро
решаете. Главное – усвоить методы научного
мышления и деятельности.
К задаче не может быть
прикладного отношения, например, просто решить
на оценку. Оценка важна, но нормы оценки вместе с
задачами тоже должны изменяться. Не надо
забывать и опыт: чтобы уметь решать задачи – надо
их решать. А значит, надо бороться за учебное
время, организовывать внеучебную деятельность,
участвовать в олимпиадном движении, турнирах
юных физиков (ТЮФах) и других формах
интеллектуальных соревнований.
Методическое построение курса
Прежде всего это структура и
содержание предлагаемого материала, т.е. задач,
примеров их решений и др.
I. Учебные физические задачи и
их решение
1. Физическая задача.
Классификация (4 ч).
Что такое физическая задача?
Состав физической задачи. Физическая теория и
решение задач. Значение задач в обучении и в
жизни.
Классификация физических
задач по требованию, содержанию, способу задания,
способу решения. Примеры задач всех видов.
Составление физических задач.
Основные требования к составлению задач. Способы
и техника составления задач. Примеры задач всех
видов.
2. Правила и приёмы решения
физических задач (6 ч).
Общие требования при решении
физических задач. Этапы решения. Работа с текстом
задачи. Анализ физического явления; формулировка
идеи решения (план решения). Выполнение плана
решения задачи. Числовой расчёт. Использование
вычислительной техники для расчётов. Анализ
решения и его значение. Оформление решения
задачи.
Типичные недостатки при
решении и его оформлении. Изучение примеров
решения задач. Различные приёмы и способы
решения физических задач: алгоритмы, аналогии,
геометрические приёмы. Метод размерностей,
графические решения и т.д.
II. Механика
3. Динамика и статика (8 ч).
4. Законы сохранения (8 ч).
III. Молекулярная физика
5. Строение и свойства газов,
жидкостей, и твёрдых тел (6 ч).
6. Основы термодинамики (6 ч).
IV. Электродинамика
7. Электрическое и магнитное
поля (5 ч).
8. Электромагнитные колебания
и волны (14 ч).
V. Квантовая физика
9. Квантовая оптика, физика
атома, атомного ядра и элементарных частиц (6 ч).
10. Наиболее общие методы
решения физических задач (10 ч).
Примеры методических решений
I. Поиск новых видов учебных
задач (или задач с новыми функциями),
например, задач с методологическим содержанием.
Образцы таких заданий и задач, их смыслы изложены
ниже.
На определение статуса
знания (понятий, законов, фактов, принципов и
т.д.). Например, задача с выбором правильного
ответа:
– в учебнике написано: «В
замкнутой системе алгебраическая сумма зарядов
всех частиц остаётся неизменной». Это
утверждение является:
А) определением явления; Б)
физическим законом; В) опытным фактом; Г)
названием явления.
– Можно ли считать
математический маятник моделью? Ответ
всесторонне обоснуйте.
– Можно ли считать моделью
наблюдаемые на экране волны, полученные в
результате отражения света от волн, бегущих по
поверхности воды?
– В чём основной недостаток
представлений о гармонической волне?
– Чем боровская модель атома
отличалась от модели атома Резерфорда?
– Каковы недостатки боровской
модели атома? Как они были преодолены?
– Как без проведения
эксперимента доказать гипотезу: я могу
свободно сдвинуть с места шкаф с книгами? Всегда
ли для доказательства гипотезы удобно
использовать экспериментальный метод? Приведите
в качестве аргументов примеры.
– Мальчик из кинофильма
«Матрица» говорит Нео: «Не пытайся согнуть
ложку. Её не существует». Можно ли аналогично
утверждать: «Не пытайтесь потрогать массу, её
нет. Не пытайтесь подышать идеальным газом, его
нет»? (Ответ. С объектами науки надо работать
как с объектами науки, а не как с реальными
объектами.)
На различные аспекты построения
научного знания: структура теории, виды знания,
функции знания и др. Например, обсуждение
вопросов типа:
– Чем отличается наблюдение
от эксперимента? (Ответ. Наблюдение –
изучение происходящих явлений в природе,
эксперимент – искусственное производство
физического явления.)
– Какие источники физических
знаний вам известны? (Ответ. Наблюдения,
эксперименты, теоретическая деятельность. При
ответе на подобные вопросы необходимо обращение
к авторитетам, цитирование работ классиков.)
– Новая физическая теория
вполне удовлетворительна, если она:
А) объясняет половину
известных фактов; Б) хорошо согласуется с
известной теорией; В) основана на здравом смысле;
Г) удобна для использования; Д) объясняет
известные факты и предсказывает новые.
На закономерностях
(особенностях) развития научного знания,
науки: абсолютность и относительность знания,
связь научного знания с практикой,
гуманистическая направленность научного знания,
роль теории в современном обществе, роль знаний в
жизни человека и др. Например:
– Известный физик, лауреат
Нобелевской премии академик В.Л.Гинзбург*
выделяет следующие особенности развития
научного знания: а) переход от
экспоненциального роста внешних показателей
научного развития на режим насыщения; б) при
относительном постоянстве условий, ресурсов
сохранение темпа роста научного знания; в)
отсутствие возможностей для сколь-либо
существенного повышения эффективности
творческой деятельности. Приведите примеры для
доказательства действия данных факторов при
производстве научных знаний.
– Каковы основные показатели
развития физики? (Ответ. Рост научных
учреждений, числа учёных, числа научных работ,
открытие новых законов и теорий…)
– Каковы основные
закономерности (черты) развития физики? (Ответ.
Социально-культурная обусловленность
возникновения знания, периоды эволюционного и
революционного развития, абсолютность и
относительность знания, поступательное развитие
научного знания, выделение фундаментального и
прикладного знания, рост влияния научного знания
на практику, процессы интеграции и
дифференциации знания, усиление ведущей роли
теоретического знания, возрастание роли
методологического знания.)
На конкретные методы и методики
научного исследования: макроскопическое и
микроскопическое описание объектов,
статистические и динамические закономерности,
системный анализ, математику как язык физики,
мысленный эксперимент и др.
На особенности экспериментального
метода познания: связь теории и опыта,
взаимодействие прибора и объекта, интерпретация
результатов эксперимента, экстраполяция и
интерполяция, проблема точности
экспериментальных данных, природа погрешностей,
приёмы расчёта погрешностей и др. Примеры:
– Для чего в научных
исследованиях стараются повысить точность
измерений?
– Почему учёные, фиксируя
результаты измерений, приводят и пределы
погрешностей измерений? Приведите примеры таких
записей.
– Каким требованиям должен
удовлетворять научный эксперимент? (Ответ.
Эксперимент должен быть воспроизводимым, иметь
цель, он всегда является модельным, предполагает
интерпретацию результатов, не позволяет сделать
абсолютные выводы.)
– Каковы особенности
мысленного эксперимента? (Ответ. Это
эксперимент с идеальными объектами или
явлениями на основе теоретических правил или
теории, эксперимент без погрешностей,
теоретическое моделирование по логике (этапам)
физического эксперимента, логический
эксперимент над понятиями, законами,
представлениями и т.п.)
На отделение объектов
природы от объектов науки, т.е. от средств
описания: объекты природы и объекты науки
(классификация), познаваемость объектов природы,
непрерывность познания, проблема выбора средств
описания, иерархия моделей, рациональное и
нерациональное знания и др. Например:
– Можно ли утверждать, что
классическая механика ошибочна, ибо она не даёт
точного описания механического движения и даже
неприменима для тел, движущихся с большими
скоростями?
– Можно ли определение границ
применимости теории считать признаком: а)
несовершенства теории; б) неверности теории?
Есть ли границы применимости у науки?
– Известный физик, лауреат
Нобелевской премии академик П.Л.Капица писал:
«Получение, преобразование и консервирование
энергии и есть фундаментальные процессы,
изучаемые физикой»**. С помощью конкретных
примеров докажите справедливость этого
утверждения.
– Согласно распространённой
модели «Большого Взрыва» Вселенной время её
существования оценивают в 1010 лет. Оцените
размеры пространства Вселенной сейчас. (Подсказка. Следует
учесть, что, согласно современным
представлениям, скорость распространения
материальных процессов не может быть больше
скорости света.)
– Опишите все физические
свойства предложенного бруска.
II. Определение отношения к
структуре и процессу решения любой задачи. Это
ключевой методический вопрос (усложнение
структуры, новые формы и др. совершенно
необходимо). Пример:
Задача. Два груза,
связанные между собой нитью, движутся по
горизонтальной гладкой поверхности. Когда к
правому грузу приложена сила 100 Н в
горизонтальном направлении, сила натяжения нити
составляет 30 Н. Каким будет натяжение нити, если
грузы поменять местами? Чему равно отношение
масс грузов?
Первый этап: анализ
физического явления
1. Два груза движутся
поступательно, значит, их можно моделировать
материальными точками. Грузы взаимодействуют
между собой, на каждый их них действует Земля,
поверхность, воздух. (Напомним, что плоская
поверхность может действовать двояко.)
2. В задаче рассматриваются два
различных случая. Они имеют между собой много
общего: одни и те же объекты, одни и те же виды
взаимодействия, действие Земли и плоскости
остаётся постоянным. (Вопрос для обсуждения:
на основании чего можно сделать такой вывод?)
Взаимодействие материальных точек (модели
грузов) в наблюдаемых случаях неодинаково. В
первом случае взаимодействие характеризуется
двумя силами, равными 30 Н каждая, противоположно
направленными и приложенными к материальным
точкам. Необходимо охарактеризовать это
взаимодействие во втором случае.
3. Сила, характеризующая
действие Земли, и сила, характеризующая реакцию
опоры, для каждого тела равны по величине и
противоположны по направлению. Они остаются
постоянными в обоих случаях. О силе трения в
задаче прямо не сказано, но, раз плоскость
гладкая, предположим отсутствие трения. (А «на
потом» заметим: изменится ли результат при
наличии трения?)
4. Итак, по условию и по
требованию это задача по динамике. В динамике
известны два метода решения: использование
законов Ньютона или законов сохранения. В нашем
случае необходимо составить уравнения движения
для системы двух тел. Описание взаимодействующих
грузов состоит из описания движения каждого
отдельного объекта уравнением второго закона
Ньютона.
5. Очевидно, что при отсутствии
значений масс тел необходимо начать решение
задачи в общем виде.
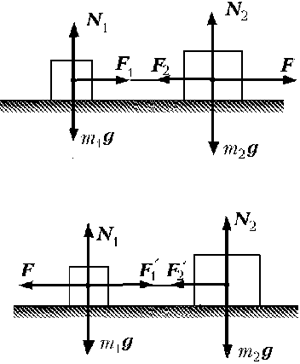
6. Выполним рисунок. Выберем
ИСО (одна ось, связанная с опорой). Введём
соответствующие обозначения. Запишем краткие
условия задачи.
1. Общей идеей решения является
описание движения двух материальных точек с
помощью законов Ньютона. С учётом третьего
закона это описание можно разделить на два:
описание движения одной материальной точки и
описание движения другой. Таким образом, получим
систему двух уравнений.
2. Для двух случаев имеем
четыре уравнения.
3. Полученные векторные
уравнения при прое-цировании на две оси системы
отсчёта дают восемь скалярных. Заметим, что из
них четыре – нулевые. Они получаются при
проецировании уравнений движения на ось Y.
Если учесть, что всегда при отсутствии движения
тела по вертикали сумма проекций сил на ось Y
равна нулю, то можно ограничиться использованием
системы отсчёта из одной оси.
1. С учётом обозначений всех
сил, действующих на грузы, строим векторные
уравнения динамики***:
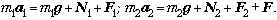
Это уравнения для первого
случая движения.
Для второго случая по аналогии
получаем:
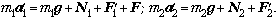
2. Записываем дополнительные
условия:
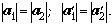
Равенство ускорений
объясняется тем, что тела связаны нерастяжимой
нитью и движутся как единое целое. По третьему
закону Ньютона, имеем:
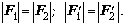
Поскольку тела находятся на
горизонтальной плоскости, по вертикали не
движутся, то сила тяжести равна по модулю силе
реакции опоры:
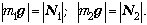
3. Проецируем на ось Х,
делаем упрощения в обозначениях:
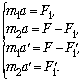
4. Применяем приём почленного
деления уравнений, что позволяет исключить
ускорения из рассмотрения. Отношение масс можно
обозначить величиной q, в результате получаем
два уравнения с двумя неизвестными:
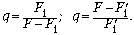
5. Приравнивая правые части,
получаем решение в общем виде:
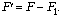
Этот ответ мы получаем также
из второго и четвёртого уравнений, если показать,
что ускорение системы тел в обоих случаях
одинаково и равно 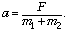 Искомое отношение масс равно
Искомое отношение масс равно
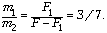
Числовой ответ: 70 Н.
1. Проанализируем решение в
общем виде. Здесь нам поможет рассуждение: «А что
будет, если...» Если модули сил F и F1
равны, то формально это равносильно отсутствию
тела m2. Последнее условие «разрушает»
задачу.
2. Если принять равным нулю
модуль одной из сил F или F1,
то ситуация будет противоречить условию и
требованию задачи. В самом деле отсутствие,
например, силы F1 равнозначно
отсутствию действия второго тела на первое.
Выводы. В центре решения
любой задачи стоит математическое описание
(моделирование) физических явлений. Вот почему,
во-первых, следует выделить нужные физические
явления, и, во-вторых, описать их физическими
законами. На первом и втором этапах решения
задачи идёт подготовка к математическому
моделированию физического явления. На третьем
этапе – работа с математической моделью. Здесь
важно правильно и умело выполнить все нужные
математические операции: составить системы
уравнений, спроецировать их на оси системы
отсчёта, произвести алгебраические
преобразования, выразить нужную физическую
величину и найти её числовое значение. Ясно, что
при выполнении всех действий нужно быть
внимательным – ошибка в каком-либо действии
делает всю остальную работу напрасной. Вот
почему следует постепенно, аккуратно выполнять
чертёж, математические действия и др. Успешное
решение любых задач требует этих качеств. Если,
например, на чертеже не указано какой-то силы, то
неправильно будет составлено уравнение, труд по
его решению окажется напрасным.
III. Поиск других, оригинальных,
способов решения задачи. В качестве примера
рассмотрим процесс решения задачи на конкретном
уроке.
Задача. На каком
максимальном расстоянии может находиться
человек, бегущий равномерно со скоростью 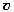 по
направлению к автобусу, который начал двигаться
в том же направлении с ускорением а, чтобы
успеть догнать автобус?
по
направлению к автобусу, который начал двигаться
в том же направлении с ускорением а, чтобы
успеть догнать автобус?
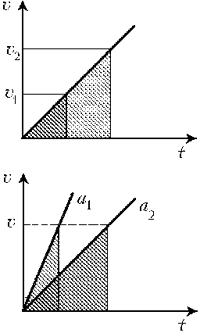
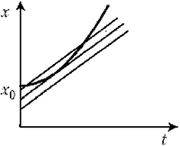
Очевидно, что, чем больше
скорость человека, тем это расстояние больше; чем
больше ускорение автобуса, тем это расстояние
меньше. Это хорошо видно из графиков, если
сравнить соответствующие площади фигур,
численно равные расстоянию. Исходя из этих
соображений, а также из анализа наименований
физических величин, можно сразу сказать, что
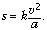
Такой анализ очень полезен для
учащихся, т.к., научившись устанавливать
физические связи между величинами, школьник
всегда сможет осознанно проверить, насколько
реален полученный ответ.
Эту задачу можно решить
графическим способом. Изобразим графики
координаты от времени для автобуса и для
пешехода. Если эти графики не пересекутся, то
пешеход никогда не догонит автобус, если
пересекутся в двух местах, то расстояние не будет
максимальным. Значит, подходит только случай,
когда график координаты от времени для пешехода
является касательной к графику координаты от
времени для автобуса. Приравняем координату
автобуса к координате пешехода:
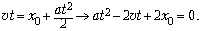
Условием единственности
решения является равенство нулю дискриминанта.
Из этого условия сразу находим искомое
расстояние:
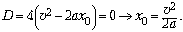
При дискриминанте, равном
нулю, х0 принимает максимальное
значение, а время, через которое человек догонит
автобус, равно t = 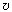 /a.
/a.
При решении различных задач
основное внимание уделяется не решению
конкретной задачи, а подходу к решению, благодаря
чему у школьников накапливается набор различных
подходов, и они уже не решают задачу полностью, а
анализируют её частями: «Нужно найти такую-то
величину. Её мы найдём, если будем знать это и это.
Это найдём, используя такой-то подход, а это
найдём, исходя из таких-то соображений...» Такое
умение видеть решение целиком очень полезно, т.к.
учащиеся осознанно находят какие-то величины, а
не уподобляются «слепым», блуждающим в
бесконечном лабиринте в поисках правильного
решения.
Поэтому, для того чтобы
ученики овладели как можно большим набором
различных подходов, после решения очередной
задачи им предлагается решить эту же задачу
каким-нибудь другим способом, Интересно, что
очень часто ребята предлагают значительно более
простые, интересные и «физичные» решения, чем
авторы задач. Приведём два решения разобранной
выше задачи, которые предложили десятиклассники
Володя и Олег (ЭСОШ № 75, г. Черноголовка).
Решение Олега. Если скорость
автобуса стала 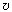 ,
а пешеход его не догнал, значит, он его вообще не
догонит, если же он догонит его раньше, то
первоначальное расстояние не будет
максимальным. Значит, время движения и автобуса,
и пешехода t =
,
а пешеход его не догнал, значит, он его вообще не
догонит, если же он догонит его раньше, то
первоначальное расстояние не будет
максимальным. Значит, время движения и автобуса,
и пешехода t = 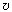 /a. Тогда
искомое расстояние x0 =
/a. Тогда
искомое расстояние x0 = 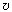 t – аt2 /2. Подставив время,
получим:
t – аt2 /2. Подставив время,
получим: 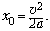
Решение Володи. Пусть
автобус неподвижен (решаем задачу в ИСО
«автобус». – Ред.). Тогда человек движется
относительно него равнозамедленно с ускорением a
и с начальной скоростью 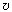 . В момент, когда координаты человека и
автобуса совпадают, относительная скорость
равна нулю, иначе они вообще не встретятся, либо
расстояние не будет максимальным. И тогда можно
сразу записать, что
. В момент, когда координаты человека и
автобуса совпадают, относительная скорость
равна нулю, иначе они вообще не встретятся, либо
расстояние не будет максимальным. И тогда можно
сразу записать, что 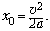
Ответ задачи, требующей для
своего решения, на первый взгляд, применения
методов высшей математики, записывается сразу
же. Однако такое решение требует не только знаний
по физике, но и глубокого её понимания. Всего
ученики нашли восемь решений этой задачи, причём
все они были подробно разобраны на доске. И хотя
подобная проработка отбирает много времени, это
время потрачено не зря, т.к., хорошо осознав тот
или иной подход к решению, ученики могут
применить его и при решении принципиально других
задач.
В настоящее время издано много
хороших сборников задач, в том числе и пособий,
готовящих к сдаче экзамена в форме ЕГЭ. Важно
помнить, что успех в формировании умений решать
задачи заключается не только в количестве
решённых задач, но и в детальном анализе решения
задач, желательно непростых, ибо, как гласит
народная мудрость, в мелкой воде плавать не
научишься.
_______________________________
* Гинзбург В.Л. Как развивается наука?
Замечания по поводу книги Т.Куна «Структура
научных революций». – Природа, 1976, № 6, с. 73–85.
** П.Л.Капица. Энергия и физика. –
Природа., 1976, № 2, с. 70–77.
*** Жирным шрифтом обозначены
векторы.– Ред.