О.Ю.ШВЕДОВ, С.Д.ВАРЛАМОВ,
Д.Э.ХАРАБАДЗЕ, И.Н.ГОРБАТЫЙ,
А.И.ЕЛАНТЬЕВ, В.А.ПОГОЖЕВ,
М.В.СЕМЁНОВ, В.В.ПАЛЮЛИН,
А.А.ЯКУТА, А.В.АНДРИАНОВ,
Е.П.АНТЫШЕВ, К.В.БАШЕВОЙ,
А.Р.ЗИЛЬБЕРМАН, Н.А.ПЕКАЛЬН
Окончание. См. № 23/05
66-я Московская региональная олимпиада
школьников по физике-2005
Второй теоретический тур
11-й класс
Задача 3
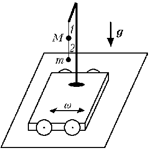
К штативу, установленному на тележке,
на лёгкой нерастяжимой нити 1 подвешен
маленький шарик массой М, к которому, в свою
очередь, на лёгкой нерастяжимой нити 2
подвешен другой маленький шарик массой m. Под
действием внешней силы, изменяющейся со временем
по гармоническому закону с частотой 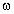 , тележка совершает малые
колебания в горизонтальном направлении. При
какой длине L нити 2 нить 1 будет всё
время оставаться строго вертикальной? Влиянием
воздуха на движение тел пренебречь.
, тележка совершает малые
колебания в горизонтальном направлении. При
какой длине L нити 2 нить 1 будет всё
время оставаться строго вертикальной? Влиянием
воздуха на движение тел пренебречь.
Решение
Если нить 1 всё время остаётся
строго вертикальной, то на систему из двух
шариков и нити 2 внешние силы в
горизонтальном направлении не действуют, и центр
масс этой системы по горизонтали не смещается.
Направим ось X горизонтально, в направлении
колебаний тележки, а начало координат поместим в
точке, где находится центр масс системы из двух
шариков: xцм = 0. Обозначим
координату шарика массой M через X(t), а
шарика массой m – через x(t), тогда mx + MX = 0.
При малых колебаниях угол 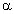 наклона нити 2 по отношению к
вертикали мал:
наклона нити 2 по отношению к
вертикали мал: 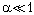 ,
так что
,
так что
sin|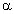 |
| 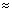 |
|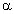 | =
| = 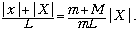
Поскольку mg 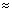 Tcos
Tcos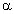
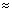 T,
где T – сила натяжения нити 2, и Tsin|
T,
где T – сила натяжения нити 2, и Tsin|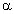 |
| 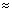 T|
T|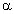 | = M
| = M = M
= M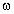 2|X|, то
2|X|, то
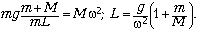
Задача 4
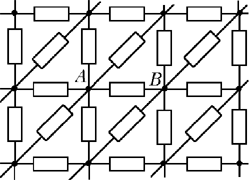
Найдите сопротивление между точками A
и B бесконечной электрической цепи в виде
сетки, схема которой изображена на рисунке. Все
резисторы в цепи одинаковые и имеют
сопротивление R.
Решение
Задача решается способом, аналогичным
применявшемуся при решении задачи 5 для 10-го
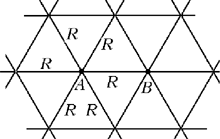
класса (2-й тур). Эквивалентная схема данной цепи
изображена на рисунке, где сопротивления всех
соединительных проводников между узлами сетки
одинаковы и равны R.
Во время измерений напряжение между
соседними узлами сетки в очень далёких точках
равно нулю. Поэтому, если мы соединим их хорошо
проводящим проводом, то ничего не изменится.
Назовём этот провод «бесконечность».
Пусть во время измерений
сопротивления напряжение между точками А и В,
измеренное идеальным вольтметром, равно U, а
ток в измерительной цепи, содержащей источник
питания и идеальный амперметр, равен I.
Возьмём теперь два одинаковых источника, каждый
из которых даёт фиксированный ток I. Первый
источник подключим к точке А и
«бесконечности» так, чтобы ток I тёк по сетке
от точки А к «бесконечности». При этом
распределение тока по разным направлениям, т.е.
по шести проводникам, подключённым к точке А,
будет равномерным, а каждый из этих токов будет
равен I/6. Второй источник подсоединим к точке В
и «бесконечности» так, чтобы он снимал с точки В
ток I, текущий к ней по сетке из
«бесконечности». В силу линейности цепи ток в
любой её точке теперь будет суммой токов двух
источников, для каждого из которых распределение
тока симметрично относительно точки, к которой
он подключён. Таким образом, при одновременном
включении обоих источников ток в проводнике,
непосредственно соединяющем точки А и В,
будет равен I/6 + I/6 = I/3, а
падение напряжения на этом проводнике равно U = R
• I/3. Поэтому сопротивление между точками A
и B данной цепи, вычисленное, как отношение
разности потенциалов U между этими точками к
току I, текущему в измерительной цепи через
каждую из этих точек, составляет U/I = R/3.
Задача 5
На высоте h над горизонтальной
плоскостью находится тонкое непроводящее кольцо
массой m и радиусом R, по которому
равномерно распределён заряд q. В момент
времени t = 0 кольцо начинает падать без
начальной скорости, сохраняя в полёте
горизонтальное положение. Одновременно с
началом падения кольца включается магнитное
поле, ось симметрии которого совпадает с осью
кольца. Вблизи кольца магнитное поле однородно,
направлено вертикально, а его индукция B
нарастает по закону B = kt2, где k –
постоянная величина. Упав на плоскость, кольцо
быстро останавливается и прилипает к ней.
Найдите количество теплоты, которое при этом
выделится в данной системе. Считать массу кольца
достаточно большой, сопротивлением воздуха
пренебречь, ускорение свободного падения равно g.
Решение
При падении кольца поток вектора
магнитной индукции через него будет изменяться,
вследствие чего возникнет вихревое
электрическое поле, силовые линии которого лежат
в плоскости кольца. Это поле будет действовать на
распределённый по кольцу заряд, и кольцо будет
раскручиваться.
Согласно закону электромагнитной
индукции Фарадея, при изменении потока Ф = BS
через кольцо площадью S = 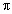 R2 возникает ЭДС
индукции
R2 возникает ЭДС
индукции 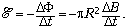 При
этом напряжённость вихревого электрического
поля, которое действует на заряды кольца, равна
При
этом напряжённость вихревого электрического
поля, которое действует на заряды кольца, равна 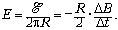 Следовательно,
раскручивающий кольцо момент сил равен
Следовательно,
раскручивающий кольцо момент сил равен
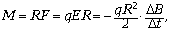
а сообщаемое им кольцу угловое
ускорение по модулю равно 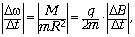 где
где 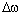 – приращение угловой скорости кольца за
малое время
– приращение угловой скорости кольца за
малое время 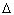 t.
Из последней формулы следует, что
t.
Из последней формулы следует, что 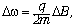 поскольку и угловая
скорость кольца
поскольку и угловая
скорость кольца 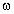 , и величина индукции магнитного поля B
возрастают со временем.
, и величина индукции магнитного поля B
возрастают со временем.
Кольцо коснётся плоскости через время 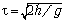 после начала
падения. За это время оно приобретёт угловую
скорость
после начала
падения. За это время оно приобретёт угловую
скорость
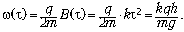
Так как по условию задачи кольцо, упав
на плоскость, быстро останавливается и прилипает
к ней, то вся приобретённая кольцом за время
падения кинетическая энергия переходит в тепло
(поскольку время торможения кольца очень мало, то
можно пренебречь работой, которую совершают за
это время над кольцом силы, действующие со
стороны вихревого поля). Значит:
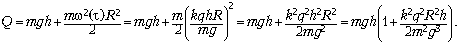
Заметим, что при решении данной задачи
можно пренебречь магнитным полем, создаваемым
вращающимся заряженным кольцом, и вкладом этого
поля в полный магнитный поток, пронизывающий
кольцо. Такое приближение обычно используется
при решении ряда аналогичных задач, например, о
падении проводящей рамки в магнитном поле или о
движении перемычки по рельсам в поле.