ПРИЁМЫ И МЕТОДЫВ.Л.ЭКЕЛЕКЯН,школа № 765, г. Москва hekevar@hotmail.com Относительность движенияМетодика решения задач. 10-й кл. Профильный уровеньВ работе представлен ряд методических рекомендаций по совокупности двух основных предметов, изучаемых в старших классах общеобразовательной школы: по физике (механика, 9-й класс) и по математике (тригонометрические преобразования, 9-й класс; математический анализ и изучение поведения функций, 10–11-й классы; метод декартовых координат, 10-й класс). Нетрудно добавить к ним и информатику (алгоритмизация конкретных физических и реальных математических задач с применением элементов программирования). Желающие могут обратиться за консультацией по составлению программ непосредственно к автору. 1. Принципы относительности В 9-м классе тему «Относительность движения» обычно проходят в разделе «Кинематика» после изучения темы «Равномерное прямолинейное движение» и перед темой «Равнопеременное прямолинейное движение». В среднем на неё, как правило, отводится один, редко – два часа. Однако тема эта узловая, т.к. в дальнейшем на её основе рассматриваются случаи больших скоростей, релятивистская механика и теория относительности Эйнштейна, смещающая теорию относительности Галилея. С другой стороны, на приёмных экзаменах в вузы предлагается много задач по кинематике, которые решаются только с применением теории относительности.
или, в декартовых координатах:
Зависимости координат от времени в системе Kот для равномерного прямолинейного движения запишутся, как обычно: 0 + y = y0 + z = z0 + где t – текущее время, x0, y0 и z0 – декартовы координаты начального положения (при t = 0) материальной точки в системе отсчёта Kот. 2. Задача об обгоне (№ 38 (37) [4])
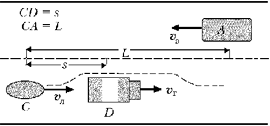
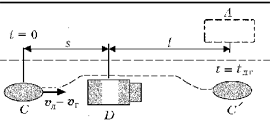
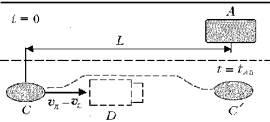
Решение. Задача решается на основе принципа относительности Галилея. Решим её в два приёма, рассматривая движение легкового автомобиля: 1) в системе отсчёта «грузовик», причём движение автобуса рассматривать не будем совсем; 2) в системе отсчёта «автобус», а движение грузовика рассматривать не будем. 1. Для определённости за положительное
направление примем направление движения
легкового автомобиля и грузовика. Тогда в
системе «грузовик» легковая машина будет
двигаться относительно грузовика со скоростью
2. Рассмотрим движение легкового
автомобиля в относительной системе отсчёта
«автобус». В ней скорость легковой машины
относительно автобуса
3. Обгон считается безопасным, если легковой автомобиль в конце обгона окажется на 20 м впереди грузовика, не доехав при этом до автобуса:
Рассчитаем минимальное расстояние между легковым автомобилем и автобусом, когда ещё можно начать обгон:
Проанализируем формулу (6). Очевидно,
что обгон возможен, если легковой автомобиль
движется быстрее грузовика: 3. Задача о преследовании [6, 7]
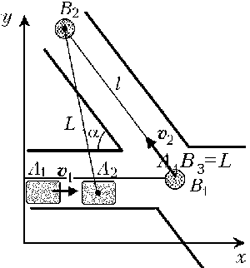
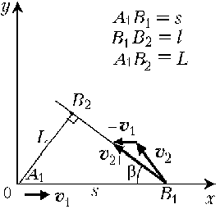
Решение. Выберем декартову систему
координат с началом отсчёта в исходном положении
автомобиля – точке А1 – и осью x,
направленной по его движению. В этой системе
отсчёта, согласно принципу относительности
Галилея, автомобиль А будет покоиться, а
автомобиль В – двигаться с относительной
скоростью 21 = – Определим направление движения
автомобиля В по отношению к автомобилю А,
введя угол
Кратчайшее расстояние между автомобилями в системе отсчёта «А» равно длине перпендикуляра, опущенного из точки А1 на прямую В1В2: l = s sin где относительная скорость
При частных значениях L = 0 ( L = L = 0 ( Время до минимального сближения
совпадает со временем прохождения автомобилем В
расстояния
Теперь можно произвести и численные расчёты (их можно произвести на «Бейсике»):
Литература 1. Ландау Л.Д., Лифшиц Е.М. Механика. – М.: Наука, 1973. 2. Ольховский И.И. Курс теоретической механики для физиков. – М.: Издательство Московского университета, 1978. 3. Голдстейн Г. Классическая механика. – М.: Гостехиздат, 1975. 4. Рымкевич А.П. Сборник задач по физике: 9–11 кл.: 14-е изд. – М.: Просвещение, 1992. 5. Соловьёв А., Карелин Р. Правила дорожного движения с комментариями в иллюстрациях. – Алма-Ата: Издательство ЦК компартии Казахстана, 1987. 6. Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. – М.: Наука, 1977. 7. Павленко Ю.Г. Начала физики. – М.: Издательство Московского университета, 1988.
|
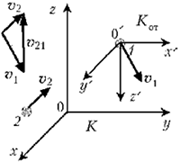 Суть вопроса заключается в
следующем: пусть материальные точки 1 и 2
движутся прямолинейно со скоростями
Суть вопроса заключается в
следующем: пусть материальные точки 1 и 2
движутся прямолинейно со скоростями