а) координаты от времени: 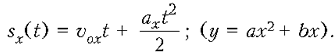
б) проекции вектора скорости от времени: vx(t)
= vox + axt; (y = kx + b);
в) проекции вектора перемещения от времени: 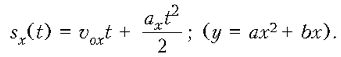
Цели урока
Ход урока
I. Вводная
Учитель. Сегодня мы повторим материал по разделу «Кинематика», а также посмотрим, как применять графики для описания механического движения. Мне бы очень хотелось, чтобы вы работали быстро, четко и дружно и показали бы во всей полноте, что вы знаете и умеете.
II. Актуализация знаний (фронтальная беседа)
Учитель. Какое движение называется механическим?
Учащиеся. Изменение положения тела относительно других тел в пространстве с течением времени.
Учитель. Как определить положение тела?
Учащиеся. Положение тела по отношению к другим телам определяется его координатами.
Учитель. Что необходимо сделать для того, чтобы определить координаты тела?
Учащиеся. Чтобы определить координаты тела, необходимо: 1) выбрать тело отсчета; 2) в зависимости от того, где тело совершает движение (прямая, плоскость или пространство) выбрать систему координат; 3) выбрать прибор для отсчета времени.
Учитель. Как называется та совокупность, которую вы только что назвали?
Учащиеся. Тело отсчета, система координат, с которым оно связано, и прибор для отсчета времени представляют собой систему отсчета, относительно которой и рассматривается движение.
Учитель. Тело совершает движение в пределах плоскости. Как определить его положение?
Учащиеся. Необходимо построить две взаимно перпендикулярные прямые с выбранными направлениями и единицей длины, которые образуют прямоугольную систему координат (координатную плоскость). Прямые углы, образуемые осями координат, называют координатными углами (квадрантами).
Учитель. Введение прямоугольной системы координат на плоскости связано с именем выдающегося французского математика XVII в. Рене Декарта (1596–1650).
(Учащиеся делают сообщения о Декарте и его работах. Одновременно на экран проецируются портрет Рене Декарта, прямоугольная система координат с квадрантами и прямоугольная система координат с обозначением координат точек и их названиями.)
Используя теоретические знания, найдите положение предложенных вам точек по их координатам. (Учащиеся одновременно работают – у доски и на своих рабочих местах, по карточкам. Затем каждый обменивается работой с соседом и дает оценку его работе.)
При решении разнообразных задач в различных областях знаний мы встречаемся с величинами, которые изменяются и значения которых зависят друг от друга. Как они называются?
Учащиеся. Такие величины называются переменными.
Учитель. Приведите примеры.
Учащиеся. Если тело совершает равномерное движение, то скорость его постоянна и пройденный путь зависит только от времени.
Учитель. Как называются эти переменные?
Учащиеся. Время t – независимая переменная (или аргумент), а путь s – зависимая переменная (или функция). Зависимость переменной s от переменной t называют функциональной зависимостью s от t: s (t).
Учитель. Как в математике обычно обозначаются переменные?
Учащиеся. Независимая переменная обозначается буквой x, а зависимая переменная – буквой y. Обычно пишут: y (x).
Учитель. Какими способами может быть задана функция?
Учащиеся. Функция может быть задана в виде формулы (аналитически), в виде таблицы и в виде графика (графически).
Учитель. Рассмотрим каждый из этих способов.
1. Аналитический. В соответствии с заданными на доске значениями составьте уравнения зависимостей различных физических величин от времени.
а) координаты от времени: x (t) = x0 + vt; (y = b + kx);
б) проекции вектора перемещения от времени: sx(t) = v t; (y = kx).
а) координаты от времени:
б) проекции вектора скорости от времени: vx(t) = vox + axt; (y = kx + b);
в) проекции вектора перемещения от времени:
(Работа по составлению уравнений. Взаимообмен и взаимооценка.)
2. Табличный – функция может быть представлена таблицей. Какая зависимость между величинами x и t; sx и t при равномерном движении?
Учащиеся. Линейная: x ~ t; sx ~ t.
Учитель. Какой график описывает линейную зависимость?
Учащиеся. Прямая.
Учитель. Сколько точек нужно для построения такого графика?
Учащиеся. Две точки.
Учитель. Чертим таблицы для построения графиков.
Какая зависимость между величинами x и t; sx и t; vx и t при равнопеременном движении?
Учащиеся. Для x и t – квадратичная: x ~ t2. Для sx и t – тоже квадратичная: sx ~ t2. Для vx и t – линейная: vx ~ t.
Учитель. Что является графиком данных функций?
Учащиеся. Зависимость между x и t описывается параболой, между sx и t – тоже параболой, между vx и t – прямой. Чтобы построить параболу, необходимо иметь значения большого числа точек.
Учитель. Заполняем таблицы значениями. (Взаимообмен и взаимооценка.)
3. Графический – функция может быть задана графиком. Для изучения механического движения используют графики скорости, координаты, перемещения, пройденного пути, ускорения.
Для равномерного движения vx = const. Что такое скорость? Это физическая величина, характеризующая быстроту движения тела. Что представляет собой график скорости для равномерного прямолинейного движения? Это прямая, параллельная оси времени. (Строит график.) По построенному графику прошу ответить: а) чему равна скорость тела через t1 c? б) чему равно перемещение тела за t2 c?
Как определить перемещение тела по данному графику?
Учащиеся. Оно определяется как площадь фигуры,
заключенной между координатными осями, графиком
функции и перпендикуляром, восстановленным из
оси времени до пересечения его с графиком
скорости (в математике ![]() ).
).
Учитель. По данным таблиц построим графики x (t) и sx(t) для равномерного прямолинейного движения. Какую информацию о движении можно из них извлечь?
Учащиеся. По значению времени можно определить координату тела или проекцию вектора перемещения. Или, наоборот, по значению координаты тела определить, в какой момент времени это произошло.
Учитель. Для равнопеременного движения аx = const. Что такое ускорение? Что представляет собой график ускорения при равнопеременном движении?
Учащиеся. Ускорение – это физическая величина, характеризующая быстроту изменения скорости. Так как для равнопеременного движения это величина постоянная, то графиком аx (t) является прямая, параллельная оси времени.
Учитель. Построим данный график. Зная начальную скорость и ускорение, составим уравнение vx(t). Изобразим и эту зависимость графически. Какую информацию можно извлечь из данного графика?
Учащиеся. Можно определить скорость в любой момент времени и перемещение тела за определенный промежуток времени. Оно определяется как площадь фигуры, заключенной между координатными осями, графиком функции и перпендикуляром, восстановленным из оси времени до пересечения его с графиком скорости.
Учитель. Какие фигуры могут получиться в итоге? Как найти их площадь?
Учащиеся. ![]()
Учитель. Перейдем к построению графиков sx(t), x(t), l(t). Для построения графика sx(t) выполняем определенный порядок действий:
1. Находим точки пересечения графика с осью t, решив уравнение типа ax2 + bx = 0:
2. Находим точку, через которую проходит ось симметрии параболы (это середина отрезка t1t2).
3. Подставляем координату этой точки в уравнение зависимости sx(t). Получаем координату вершины параболы.
4. Чертим параболу. В зависимости от начальной координаты график x(t) строим путем смещения вдоль оси х вверх или вниз. График l(t) строим путем симметричного отображения ниспадающей ветви параболы – так, чтобы функция получилась возрастающей.
Очень часто при изображении двух или более графиков можно увидеть пересечение кривых. Что оно означает?
Учащиеся. Для графиков скорости это означает момент времени, когда скорости одинаковые, для графиков движения – время и место встречи.
Учитель. Используя свое уравнение движения и уравнение, полученное соседом, найдите по графику время и место встречи тел, совершающих движение. (Взаимообмен, контроль и проверка.)
Очень часто для определения различных физических величин используют понятие производной. Попробуем и мы его использовать. Запишите, чему равны производные простейших функций:
![]()
а также, что v(t) = s'(t); v(t) = x'(t); a(t) = v'(t) = s''(t). Найдите скорость и ускорение движения точки в момент времени t = 5 c, если задано уравнение зависимости x (t). (Решение задачи.)
Подведем итоги урока!..
С.Е.Тихомирова работает по программе Г.Н.Степановой