Физика повсюдуФизика повсюдуПетарды
Каких только петард сейчас нет! И жужжащие, и свистящие, и стреляющие разноцветными ракетами, есть и просто «хлопушки» – в общем, выбор огромен! Среди хлопушек, выпускаемых самыми разными заводами, появились и такие, которые производят достаточно громкий звук, но вполне безопасны с точки зрения катастрофических последствий. Ими мы и займемся.
Правильно изготовленная петарда после поджига оставляет пользователю (терминология совсем как в вычислительной технике!) некоторое время на то, чтобы отбросить ее подальше от себя или успеть отойти на два-три шага. Затем следует взрыв. Мы не будем обсуждать химические реакции, для нас важно, что в малом объеме очень быстро возникает разогретый газ, который, расширяясь, и создает звук. За звук мы, собственно, и платим, покупая петарду!
Взрывная волна распространяется по взрывчатому веществу достаточно быстро: при длине цилиндра около 5 см время взрыва не превышает 10–5 с. Я своим ученикам при изучении газовых законов демонстрирую полет жестяной консервной банки, под которой взрывается петарда. Сначала мы обсуждаем, что произойдет, если в газе, ограниченном стенками банки, выделится большое количество тепла. Затем обращаем внимание на то, что дна у банки нет и она не закреплена на полу. Выясняем «судьбу» горячего газа, возникшего внутри. После всестороннего обмена мнениями выясняем, что разгоняться банка будет на небольшом расстоянии, пока горячий газ не вылетит через возникший между краями банки и полом зазор. Затем банка полетит вверх за счет приобретенной на этапе разгона скорости. На какой-то высоте она остановится на мгновение и полетит вниз. Измерить мы можем высоту подъема банки, ее размер и массу. А какое же было давление на стенки банки после взрыва?
Эксперимент. Рассматриваются два случая. В первом случае в начальный момент края банки плотно прилегают к гладкому полу (или столу), во втором создается зазор толщиной примерно 2 мм (под край банки кладем три спички). Банка длиной L = 10 см, диаметром D = 7 см и массой m = 50 г при взрыве петарды «Корсар-1» (длина картонного корпуса-цилиндра 4 см, диаметр 5 мм) взлетает в первом случае примерно на Н = 2 м, во втором – примерно на 70 см.
Разобьем движение банки после взрыва на два этапа. Разгон происходит на небольшом расстоянии (для оценки подойдет 2 мм). Действительно, если создан начальный зазор 2 мм, то банка взлетает на высоту, в три раза меньшую, чем без зазора.
Скорость банки в конце участка разгона равна
примерно 
Эта
скорость гораздо меньше скорости звука в воздухе
и тем более скорости взрывной волны во
взрывчатом веществе.
Простая модель. Если предположить, что на всем
пути в 2 мм на дно банки действовала постоянная по
величине сила, а все остальное время на банку
действовала только сила тяжести, то очевидно, что
одна сила совершила на пути 2 мм положительную
работу и увеличила скорость и кинетическую
энергию банки, а вторая сила на пути 2 м совершила
отрицательную работу, и кинетическая энергия
банки опять (в верхней точке) стала равной нулю.
Отношение расстояний
Отсюда можно оценить среднее давление, которое газы оказывали изнутри на дно банки. Это давление было больше внешнего атмосферного давления на величину
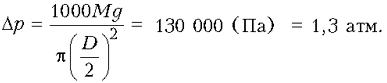
Проведенная оценка – это первое и достаточно грубое приближение. Конечно же, давление не сохранялось во времени. По мере подъема банки воздух из-под нее вырывался наружу и поэтому очевидно, что самым большим давление было только сразу после взрыва петарды, а затем становилось все меньше и меньше.
Модель посложнее. Внутренний объем банки около 380 мл. Масса воздуха в этом объеме примерно равна 0,5 г. Внутренний диаметр корпуса петарды составляет примерно 2 мм. Из этого следует, что объем взрывчатого вещества, находящегося в петарде в виде смеси порошков (крупинок) разных веществ, не превышает 100 мм3, а его масса составляет около 0,1 г.
Продукты сгорания, как правило, имеют молекулярную массу, значительно большую, чем газы воздуха. Таким образом, можно считать, что масса газов под банкой сразу после взрыва практически не отличается от массы воздуха. То есть можно сказать, что воздух в банке внезапно нагрелся и его давление повысилось, а плотность воздуха осталась прежней.
Время движения банки, в течение которого нам
интересно поведение горячего воздуха,
составляет примерно
В соответствии с известным уравнением Пуассона для адиабатического процесса давление p и плотность газа r связаны соотношением
Здесь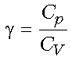 
–
отношение молярной теплоемкости газа в процессе
с постоянным давлением к молярной теплоемкости
того же газа в процессе с постоянным объемом. Для
воздуха, который в основном состоит из
двухатомных молекул кислорода и азота, эта
величина равна 7/5.
Ускоряться банка перестает в тот момент времени t, когда давление внутри сравнивается с наружным давлением:
p (t) = p0. (2)
Плотность газа сразу после взрыва была равна плотности окружающего банку воздуха. По мере подъема банки воздух из-под нее выходит. Скорость u истечения газа через зазор может быть оценена с использованием уравнения Бернулли:
Уравнение, описывающее изменение плотности газа под банкой со временем, таково:
где х – текущая ширина зазора.
Уравнение движения банки в соответствии со вторым законом Ньютона таково:
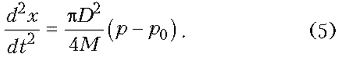
Начальное значение х = 0. Начальное значение
плотности воздуха равно плотности окружающего
банку воздуха
Скорость банки в конце участка разгона можно получить интегрированием (силой тяжести во время разгона пренебрегаем):
Теперь нужно подобрать такое начальное давление газа сразу после взрыва, чтобы в результате расчетов в соответствии с уравнениями (1, 3–6) при конечном значении давления газа, равном атмосферному по условию (2), скорость банки была бы равна 6,3 м/с.
Как понимают читатели, это задача для терпеливых и умеющих обращаться с компьютером. Впереди нас ждут весенние каникулы. Вот, может быть, кто-нибудь из читателей газеты, учителей физики, вместе со своими учениками за время каникул решит такую задачу? В этом случае просьба: сообщите, пожалуйста, мне полученную величину максимального давления воздуха в банке. (Надеюсь, за указанное время я тоже проведу расчеты!) Сравним наши результаты!