 системы координат,
показанной на рис. 2, должны быть равны:
системы координат,
показанной на рис. 2, должны быть равны:В 2002 г. на физическом факультете Московского государственного университета им. М.В.Ломоносова проводилась в два тура физико-математическая олимпиада (в марте и мае) и один вступительный экзамен (в начале июля). Олимпиадные задания и экзаменационные билеты по физике содержали два теоретических вопроса, формулировки которых были взяты из программы по физике, опубликованной в справочнике для поступающих в МГУ, и две задачи. Абитуриенты, получившие на олимпиаде по математике и физике не менее 13 баллов (максимальная оценка по физике – 10 баллов, математике – 5 баллов) были приглашены для учебы на факультете. Ниже приводятся условия предлагавшихся задач и их решения. В решениях особое внимание уделено обоснованию возможности применения того или иного закона и указаны предположения, в том числе и так называемые стандартные, которые необходимо было сделать в ходе решения. По всем вопросам приема просим обращаться по телефону: 939-1241 (Cовет по новому приему и работе со школьниками физического факультета МГУ).
I. МЕХАНИКА
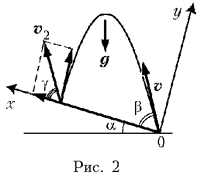
1. Из некоторой точки плоскости, образующей с горизонтом угол a = 30°, бросают упругий шарик (рис. 1). Зная, что место второго удара шарика о плоскость находится выше места его первого удара, найти возможные значения угла бросания этого шарика относительно горизонта.
Решение
При решении задачи будем пренебрегать влиянием
воздуха на движущийся шарик и изменением
ускорения свободного падения с высотой. Кроме
того, будем считать, что система отсчета,
неподвижная относительно плоскости, является
инерциальной. При сделанных предположениях,
согласно второму закону Ньютона, проекции
ускорения шарика после броска (момент времени t =
0) и до момента его первого удара о плоскость (t = t1) на оси  системы координат,
показанной на рис. 2, должны быть равны:
системы координат,
показанной на рис. 2, должны быть равны:
![]()
Из этих соотношений следует, что при начальной скорости шарика равной v, он первый раз коснется плоскости в момент времени
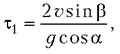
где b – угол наклона скорости v шарика к плоскости, а g – величина ускорения свободного падения. Из сказанного следует, что непосредственно перед первым ударом о плоскость проекции скорости шарика наоси выбранной системы координат должны быть равны:
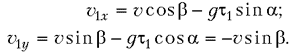
По условию задачи, шарик является упругим. Следовательно, можно утверждать, что непосредственно после первого удара х-составляющая скорости шарика v2x должна быть равна v1x. Считая же массу плоскости много больше массы шарика, на основании закона сохранения механической энергии и закона сохранения импульса можно доказать, что непосредственно после удара v2y = –v1y = v sin b.
Поскольку точка второго удара, по условию
задачи, должна быть расположена выше точки
первого удара, скорость шарика сразу после
первого удара должна быть направлена
относительно плоскости под углом,
удовлетворяющим условию ![]() а поэтому
а поэтому
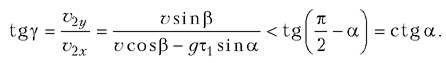
Отсюда следует, что ![]() Поскольку искомый угол
Поскольку искомый угол ![]() допустимые значения этого
угла должны удовлетворять условию
допустимые значения этого
угла должны удовлетворять условию ![]() т.е.
т.е. ![]()
2. За бегущей прямолинейно со скоростью vл = 45 км/ч лисой гонится собака. Скорость собаки все время направлена на лису и равна vс = 55 км/ч. В некоторый момент времени t скорость собаки оказалась перпендикулярной скорости лисы, а расстояние между ними стало равным L = 150 м. Найдите ускорение собаки в этот момент времени.
Решение
По условию задачи, величина скорости собаки все время остается неизменной, и собака бежит все время так, что ее нос направлен точно на лису. Поэтому можно утверждать, что проекция вектора скорости собаки на положительное направление касательной к ее траектории в точке, через которую пробегает собака, все время остается постоянной, т.е. собака вдоль траектории движется равномерно, а потому тангенциальная составляющая вектора ее ускорения равна нулю. В то же время ясно, что траектория движения собаки является криволинейной. Поскольку при произвольном движении точки вектор ее ускорения может иметь только две отличные от нуля компоненты – нормальную и тангенциальную, – при заданном движении модуль вектора ускорения собаки должен быть равен его нормальной составляющей. Из кинематики известно, что величина нормальной составляющей ускорения в данной точке траектории равна отношению квадрата скорости движущейся точки к радиусу кривизны траектории в этой точке. На рис. 3 показаны положения лисы (точки 1 и 2) и собаки (точки 3 и 4) в моменты времени t и t + t, где t – столь малый промежуток времени, что отрезок траектории, который пробежала собака за время t, практически неотличим от дуги окружности. Как известно, радиус R этой окружности и называют радиусом кривизны траектории в рассматриваемой области.
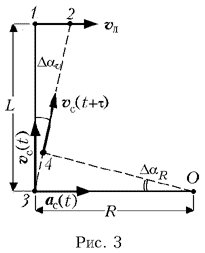
За малый промежуток времени t лиса переместилась на расстояние vлt. Следовательно, по условию задачи, направление скорости собаки должно было измениться на некоторый малый угол Dav. Если этот угол измерять в радианах, то с учетом обозначений, использованных на рис. 3, можно утверждать, что vлt»LDav. За этот же промежуток времени собака пробежала расстояние vct, двигаясь по дуге касательной окружности, а радиус этой окружности, проведенный в точку нахождения собаки, повернулся на такой угол DaR, что vct»RDaR. Поскольку DaR=Dav (как углы со взаимно перпендикулярными сторонами, явно не дополняющие друг друга до прямого угла), то в интересующий нас момент времени радиус кривизны траектории собаки равен R=L(vc/vл), а ее ускорение совпадает по направлению со скоростью лисы и равно по модулю
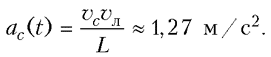
 3.
На тяжелый диск радиусом R намотаны две
нерастяжимые нити, свободные концы которых
прикреплены к потолку в точках А и В так, что
3.
На тяжелый диск радиусом R намотаны две
нерастяжимые нити, свободные концы которых
прикреплены к потолку в точках А и В так, что
нити лежат в одной вертикальной плоскости с диском (рис. 4). Найдите скорость движения центра диска в тот момент, когда угол между прямолинейными отрезками нитей АС и BD станет равным a, а угловая скорость диска будет равна w. При этом нити натянуты, а ось диска все время движется, не изменяя своего направления.
Решение
По условию задачи, ось диска движется, не изменяя своего направления. Следовательно, диск совершает плоское движение. Поэтому, считая, как это обычно и делается при решении подобных задач, диск твердым телом, движение любой его точки можно представить как сумму двух движений: вращения вокруг оси диска и поступательного движения. Как известно, линейная скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, направлена перпендикулярно радиусу вращения этой точки, а ее величина равна произведению угловой скорости на радиус вращения рассматриваемой точки. При поступательном же движении скорости всех точек твердого тела одинаковы. Из сказанного следует, что линейные скорости точек диска, совпадающих с точками С и D нити (по условию, нити тонкие), должны удовлетворять соотношениям:
![]()
где v – скорость движения оси диска, а vврС
и vврD – линейные скорости точек диска С и D
относительно оси диска, причем ![]()
С другой стороны, поскольку нити нерастяжимы,
прикреплены к неподвижным точкам потолка А и В, а
их отрезки, не лежащие на диске, по условию
задачи, прямолинейны, можно утверждать, что любая
точка этих отрезков может двигаться лишь по дуге
окружности. Следовательно, скорость любой из
указанных точек, в том числе и скорости крайних
точек С и D указанных отрезков, могут быть
направлены лишь перпендикулярно отрезкам нити
АС и BD соответственно, т.е. ![]()
Я сно,
что ответ на поставленный в задаче вопрос
зависит от того, скользят ли нити по диску при его
движении. Поскольку в условии задачи специально
это не оговорено, то, как обычно, будем
рассматривать простейший случай: скольжения
нитей по диску нет. В этом случае точки нитей С и D
неподвижны относительно соответствующих точек
диска, и поэтому относительно потолка скорости
указанных точек диска С и D равны, соответственно
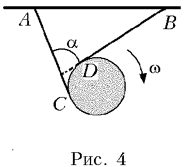
vC и vD. На рис. 5 показаны треугольники
скоростей точек С и D и расположение отрезков
нитей АС и BD относительно вектора скорости v оси
диска.
сно,
что ответ на поставленный в задаче вопрос
зависит от того, скользят ли нити по диску при его
движении. Поскольку в условии задачи специально
это не оговорено, то, как обычно, будем
рассматривать простейший случай: скольжения
нитей по диску нет. В этом случае точки нитей С и D
неподвижны относительно соответствующих точек
диска, и поэтому относительно потолка скорости
указанных точек диска С и D равны, соответственно
vC и vD. На рис. 5 показаны треугольники
скоростей точек С и D и расположение отрезков
нитей АС и BD относительно вектора скорости v оси
диска.
Выше было установлено, что
![]()
и ![]() . Поэтому
треугольники скоростей являются прямоугольными
и равными друг другу по гипотенузе и катету.
Следовательно,
. Поэтому
треугольники скоростей являются прямоугольными
и равными друг другу по гипотенузе и катету.
Следовательно,
![]()
Отсюда, в свою очередь, следует, что искомая скорость v оси диска направлена вниз по биссектрисе угла, а ее величина равна
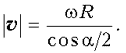
4. На закрепленной гладкой наклонной плоскости, образующей с горизонтом угол a, удерживают достаточно длинную доску массой М, на которой покоится груз массой m. В некоторый момент доску отпускают, а груз начинают тянуть вверх с постоянной силой F, направленной вдоль наклонной плоскости перпендикулярно ее ребру. При этом доска остается неподвижной, а груз скользит по ней. На сколько сместится груз к тому моменту, когда его скорость станет равной v?
Решение
Будем решать задачу, полагая, что доска, груз и наклонная плоскость – твердые тела. Кроме того, будем считать, что груз при скольжении движется поступательно. Поскольку при удерживаемой неподвижно доске груз покоится на ней, то можно утверждать, что между доской и грузом действуют силы трения. По условию задачи, когда груз начинают тянуть вверх, то доска остается неподвижной, а груз начинает скользить по ней. Следовательно, под действием силы F груз получает некоторое ускорение а, направленное вверх вдоль наклонной плоскости, перпендикулярно ее ребру, а на доску со стороны груза действует такая сила F1, что результирующая всех сил, приложенных к доске, оказывается равной нулю. Конечно, сказанное верно в предположении, что неподвижная относительно наклонной плоскости система отсчета является инерциальной, а доска имеет форму прямоугольного параллелепипеда.
Для решения задачи воспользуемся системой координат, ось y которой направлена перпендикулярно наклонной плоскости вниз, а ось x сонаправлена с силой F. Если, как это обычно и делается при решении подобных задач, силу реакции доски на груз представить в виде суммы нормальной N1 и тангенциальной Ft1 составляющих, то уравнение движения груза в соответствии со вторым законом Ньютона можно представить в виде:
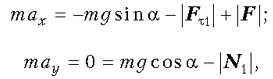
где g – величина ускорения свободного падения. Здесь учтено, что в соответствии со сказанным ранее груз после приложения к нему силы F должен двигаться вверх по доске, а потому действующая на груз со стороны доски сила сухого трения Ft1 направлена противоположно силе F.
По условию задачи, наклонная плоскость гладкая. Поэтому действующая с ее стороны на доску сила может быть направлена только перпендикулярно поверхности доски. Учитывая, что, согласно третьему закону Ньютона, силы взаимодействия груза и доски равны по величине и направлены в противоположные стороны, а доска после отпускания остается неподвижной относительно инерциальной системы отсчета, уравнение движения доски в проекции на ось x можно представить в виде:
![]()
Из приведенных уравнений следует, что проекция ускорения груза на ось x при соблюдении сделанных выше предположений равна
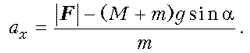
Из этого выражения следует, что груз может скользить по доске только при условии
![]()
а величина его ускорения в процессе движения остается постоянной. Поэтому проекция скорости груза на ось x и приращение его координаты х со временем должны удовлетворять соотношениям
![]()
а потому искомое смещение груза должно быть равно
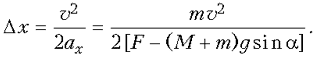
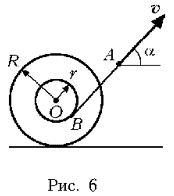 5.
Катушку (рис. 6), лежащую на горизонтальной
плоскости, тянут за намотанную на ее среднюю
часть легкую нерастяжимую нить так, что ее конец
(точка А) движется со скоростью v под углом a=30° к горизонту. При этом катушка
катится без проскальзывания, а ее ось не изменяет
своего направления. Найдите скорость движения
оси катушки, если радиус r средней части катушки в
n = 2 раза меньше радиуса R ее щек.
5.
Катушку (рис. 6), лежащую на горизонтальной
плоскости, тянут за намотанную на ее среднюю
часть легкую нерастяжимую нить так, что ее конец
(точка А) движется со скоростью v под углом a=30° к горизонту. При этом катушка
катится без проскальзывания, а ее ось не изменяет
своего направления. Найдите скорость движения
оси катушки, если радиус r средней части катушки в
n = 2 раза меньше радиуса R ее щек.
Решение
По условию задачи, при движении точки А нити
катушка катится без проскальзывания, сохраняя
направление своей оси. Следовательно, считая, как
это обычно и делается в подобных задачах, катушку
твердым телом, ее движение можно представить как
сумму поступательного движения со скоростью u и
вращения с некоторой угловой скоростью вокруг
этой оси. Катушка катится без проскальзывания,
поэтому геометрическое место точек касания
катушкой плоскости (считаем, конечно, плоскость
абсолютно твердой) является мгновенной осью
вращения, а величина угловой скорости вращения
катушки ![]() Участок
нити между точкой ее касания средней частью
катушки (точка В) и точкой А можно считать
прямолинейным, т.к., по условию задачи, массой
нити следует пренебречь. Поэтому можно
утверждать, что сила натяжения нити Т в момент
начала движения катушки должна образовывать с
горизонтом тот же угол, что и касательная к нити в
точке А.
Участок
нити между точкой ее касания средней частью
катушки (точка В) и точкой А можно считать
прямолинейным, т.к., по условию задачи, массой
нити следует пренебречь. Поэтому можно
утверждать, что сила натяжения нити Т в момент
начала движения катушки должна образовывать с
горизонтом тот же угол, что и касательная к нити в
точке А. 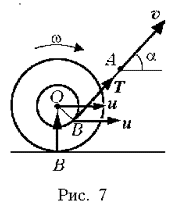 Поскольку иное специально не оговорено в
условии задачи, будем считать указанный отрезок
нити целиком расположенным в вертикальной
плоскости, перпендикулярной оси катушки. Тогда
при заданной величине угла a и заданном
соотношении радиусов щек и центральной части
катушки, как это видно из рис. 7, момент силы
натяжения нити Т должен заставить катушку
вращаться по часовой стрелке. Следовательно,
учитывая нерастяжимость нити, можно утверждать,
что величина скорости точек прямолинейного
участка нити v=ucosa-wr.Отсюда
с учетом ранее написанного соотношения находим
величину искомой скорости движения оси катушки
Поскольку иное специально не оговорено в
условии задачи, будем считать указанный отрезок
нити целиком расположенным в вертикальной
плоскости, перпендикулярной оси катушки. Тогда
при заданной величине угла a и заданном
соотношении радиусов щек и центральной части
катушки, как это видно из рис. 7, момент силы
натяжения нити Т должен заставить катушку
вращаться по часовой стрелке. Следовательно,
учитывая нерастяжимость нити, можно утверждать,
что величина скорости точек прямолинейного
участка нити v=ucosa-wr.Отсюда
с учетом ранее написанного соотношения находим
величину искомой скорости движения оси катушки
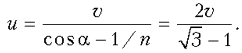
6. Через блок, закрепленный на краю горизонтальной крышки стола, переброшена гладкая легкая нить, к одному концу которой прикреплен груз массой m, а к другому – лежащий на доске кубик массой 2m, удерживаемый с доской. Передняя грань кубика находится на расстоянии s от края доски массой 3m (рис. 8). Коэффициент трения кубика о доску равен m1, доски о крышку стола – m2. За какое время t после отпускания кубик сместится к краю доски, если доска скользит по столу и за время t не достигает блока?
Решение
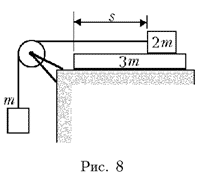 При
решении задачи будем, как это обычно и делается,
если в условии задачи нет специальных указаний,
пренебрегать влиянием воздуха и считать
лабораторную систему отсчета, относительно
которой покоится стол, инерциальной. Кроме того,
будем считать, что нить располагается в
вертикальной плоскости, проходящей через центры
масс кубика и доски, доска имеет форму
прямоугольного параллелепипеда, длинные ребра
которого параллельны названной вертикальной
плоскости. При выполнении этих предположений
можно утверждать, что после отпускания груз,
кубик и доска будут двигаться поступательно.
При
решении задачи будем, как это обычно и делается,
если в условии задачи нет специальных указаний,
пренебрегать влиянием воздуха и считать
лабораторную систему отсчета, относительно
которой покоится стол, инерциальной. Кроме того,
будем считать, что нить располагается в
вертикальной плоскости, проходящей через центры
масс кубика и доски, доска имеет форму
прямоугольного параллелепипеда, длинные ребра
которого параллельны названной вертикальной
плоскости. При выполнении этих предположений
можно утверждать, что после отпускания груз,
кубик и доска будут двигаться поступательно.
В условии задачи не оговариваются упругие свойства заданных тел. Поэтому из всех возможных вариантов будем рассматривать простейший случай: нить будем считать нерастяжимой, а все остальные тела твердыми. Кроме того, будем считать, что точка крепления нити к кубику и точка, в которой верхний отрезок нити касается блока, находятся на одной высоте. Тогда, пренебрегая в соответствии с условием задачи массой нити, можно утверждать, что верхний отрезок нити, не лежащий на блоке, при движении тел остается горизонтальным, а отрезок нити между грузом и нижней точкой касания нитью блока остается вертикальным. Поскольку нить гладкая, то силами трения между нитью и блоком следует пренебречь. Поэтому можно считать, что при движении тел блок не вращается, а потому длина отрезка нити, лежащая на блоке, остается неизменной. Отсюда с учетом ранее сделанных предположений следует, что величины ускорений груза и кубика должны быть одинаковыми. Одинаковыми должны быть и величины сил, с которыми нить действует на груз и кубик.
По условию задачи, после отпускания доска скользит по столу. Следовательно, груз будет опускаться вертикально вниз с ускорением а, удовлетворяющим уравнению
![]()
где g – ускорение свободного падения, а Т – сила, действующая на груз со стороны нити.
Кроме силы натяжения нити на кубик действует сила тяжести и сила реакции доски. Силу реакции доски на кубик, как обычно, представим в виде двух составляющих – нормальной N и тангенциальной Fт, называемой обычно силой сухого трения. Поскольку кубик в соответствии со сделанными предположениями может двигаться лишь в горизонтальном направлении, то N = –2mg. По условию задачи, кубик, первоначально удерживавшийся неподвижным вместе с доской, после отпускания за время t должен переместиться относительно стола на расстояние, превышающее перемещение доски. Следовательно, сила трения, действующая на кубик при его движении со стороны доски, является силой сухого трения скольжения, величина которой в соответствии с законом Кулона–Амонтона и условием задачи равна Ft = m1N. Из сказанного выше и второго закона Ньютона следует, что уравнение движения кубика в проекции на направление его перемещения можно представить в виде:
![]()
Рассуждая аналогично, можно доказать, что с учетом сделанных предположений уравнение движения доски в проекции на направление ее движения после отпускания должно иметь вид
![]()
где ад – проекция ускорения доски на направление ее движения.
Поскольку кубик относительно доски после их отпускания должен за время t переместиться на расстояние s, двигаясь с относительным ускорением aотн = а – ад, то искомое время должно быть равно
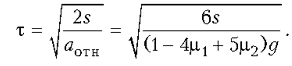
Отметим, что этот ответ справедлив при условии, что . Если же это неравенство не выполняется, то задача не имеет решения, т.к. в этом случае кубик не может скользить по доске.
7. На горизонтальной
плоскости удерживают клин. При этом груз,
подвешенный на нити к оси подвижного блока, 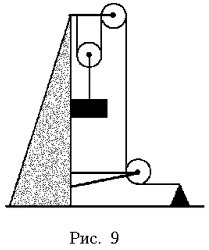 касается
вертикальной грани клина (рис. 9). Подвижный блок
висит на нити, один конец которой прикреплен к
клину, а другой – к неподвижной опоре. Масса
груза в n раз меньше массы клина. Коэффициент
трения между клином и грузом равен m.
Пренебрегая силами трения между остальными
телами, массой нитей и блоков, найдите ускорение
клина после его отпускания, зная, что клин и груз
движутся поступательно, все нити нерастяжимы, их
отрезки, не лежащие на блоках, либо
горизонтальны, либо вертикальны.
касается
вертикальной грани клина (рис. 9). Подвижный блок
висит на нити, один конец которой прикреплен к
клину, а другой – к неподвижной опоре. Масса
груза в n раз меньше массы клина. Коэффициент
трения между клином и грузом равен m.
Пренебрегая силами трения между остальными
телами, массой нитей и блоков, найдите ускорение
клина после его отпускания, зная, что клин и груз
движутся поступательно, все нити нерастяжимы, их
отрезки, не лежащие на блоках, либо
горизонтальны, либо вертикальны.
Решение
Будем считать плоскость, по которой движется клин, покоящейся относительно инерциального наблюдателя. По условию, пренебрежем силами трения нити о блоки и массой нитей. Конечно, пренебрежем и влиянием воздуха на тела рассматриваемой системы. При этих условиях величина Т силы натяжения нити, связывающей клин с неподвижной опорой, должна оставаться неизменной вдоль всей нити.
После отпускания клина груз может лишь
опускаться, а клин, двигаясь поступательно
вместе с прикрепленными к нему блоками, должен
приближаться к неподвижной опоре, действуя с
определенной силой на груз. Силу реакции клина на
груз представим в виде двух составляющих:
нормальной N, направленной горизонтально, и
тангенциальной. Согласно закону
Кулона–Амонтона, величина тангенциальной
составляющей, называемой силой 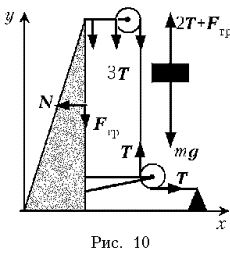 сухого трения
скольжения, равна mN, а т.к. груз
опускается, эта составляющая направлена
вертикально вверх. На груз, кроме силы реакции
клина, действует направленная вертикально вниз
сила тяжести, величина которой равна mg, и сила
натяжения нити, связывающей груз с осью
подвижного блока. На основании второго закона
Ньютона можно утверждать, что сумма сил,
действующих на подвижный блок, должна быть равна
нулю, а потому на груз со стороны нити должна
действовать направленная вертикально вверх сила
натяжения, величина которой равна 2Т. На рис. 10
жирными стрелками показаны силы, действующие на
груз, и силы, приложенные к клину с блоками со
стороны нити и груза, а рядом со стрелками
указаны величины сил. На этом же рисунке показана
и используемая при решении задачи система
координат.
сухого трения
скольжения, равна mN, а т.к. груз
опускается, эта составляющая направлена
вертикально вверх. На груз, кроме силы реакции
клина, действует направленная вертикально вниз
сила тяжести, величина которой равна mg, и сила
натяжения нити, связывающей груз с осью
подвижного блока. На основании второго закона
Ньютона можно утверждать, что сумма сил,
действующих на подвижный блок, должна быть равна
нулю, а потому на груз со стороны нити должна
действовать направленная вертикально вверх сила
натяжения, величина которой равна 2Т. На рис. 10
жирными стрелками показаны силы, действующие на
груз, и силы, приложенные к клину с блоками со
стороны нити и груза, а рядом со стрелками
указаны величины сил. На этом же рисунке показана
и используемая при решении задачи система
координат.
Учитывая, что груз до отпускания клина касался его вертикальной грани, а, по условию задачи, груз и клин движутся поступательно, можно утверждать, что проекции ах ускорений этих тел на ось x должны быть одинаковыми и удовлетворять уравнениям:
![]()
где М – масса клина (массами блоков пренебрегаем).
Поэтому проекция аy ускорения груза на ось y может быть определена из уравнения
![]()
Система уравнений (1) и (2) не является полной. Недостающее уравнение можно получить из кинематических соображений. Действительно, пусть в момент времени t, соответствующий движению тел при натянутых нитях, некоторая точка груза имеет координаты x(t) и y(t). Учитывая, что, по условию задачи, нити являются нерастяжимыми и их отрезки, не лежащие на блоках, либо горизонтальны, либо вертикальны, для рассматриваемых моментов времени можно утверждать, что 2y(t) + x(t) = const, а потому
![]()
Решая совместно уравнения (1)–(3) и учитывая, что, по условию задачи M/m=n, находим искомую величину ускорения клина:
![]()