Персональный компьютер (РС), который недавно отметил свое двадцатилетие, превратился в эпоху Интернета из средства производства информации в средство доступа к ней (во многих изданиях этот термин уже заменил РС). Компьютер – не просто шедевр современной высокой технологии, это широко рспахнутая дверь в мир информации. РС в образовании – это устройство, просто провоцирующее и учителя, и ученика на творчество и новаторство, дающее возможность перейти к креативным формам обучения.
Повышение эффективности образования невозможно без создания новых форм обучения. В связи с этим большое внимание сегодня уделяется проектной деятельности учащихся. Самостоятельная работа учащихся с компьютером, работа над самим информационным объектом, использование материалов различных CD, ресурсов Интернета, некоторых программ и утилит позволяет быстро создавать небольшие собственные работы (эссе). Именно небольшие, хотя многие учителя ставят в проектной деятельности перед учащимися очень большие задачи, перегружают детей. В этом случае разумнее руководствоваться английской пословицей «Think big, act small» (Думая о большом, делай понемногу). Одна-две странички самостоятельной работы учащегося всегда ценнее многостраничного иллюстрированного реферата, «скачанного» из Интернета.
В сети имеется много программных продуктов, которые учителя-предметники могут использовать при проведении уроков с применением новых информационных технологий. Подобные современные уроки позволяют повысить интерес к изучению предметов естественно-математического цикла, активизировать их познавательную деятельность, способствуют формированию научного мировоззрения.
Ниже мы рассмотрим возможность использования программы «Advanced Grafer» (кратко «Agrafer», версия 1.62, выпуск 1998–2000 гг., автор Michael Serpik) на интегрированных уроках физики и информатики. Этот продукт в России в случае некоммерческого использования можно получить бесплатно ( http://www.serpik.com/agrafer/ ).
Программа предоставляет очень широкие возможности. С ее помощью по имеющейся функциональной зависимости можно построить график и провести его анализ: определить максимумы и минимумы функции, найти точки его пересечения с осями и другими графиками, построить касательную и перпендикуляр к кривой в любой точке графика, определить производную функции и построить ее график, для любого интервала изменения аргумента определить интеграл функции и многое другое.
Программа также допускает параметрическое задание переменных, использование как обычных декартовых осей координат, так и полярных. Широки ее возможности по оформлению графиков: разнообразное изменение масштаба, использование логарифмической и тригонометрической шкал значений, вставка графиков и их названий, формирование пояснений в режиме вставки кадра в любой точке графика, просмотр любой части графика с произвольной детализацией. Имеется большой набор типовых графиков, пригодных для демонстрации на уроках. Разумеется, полученные графики можно сохранить в файле и затребовать их из файла для использования. Рабочее поле можно также сохранить как точечный рисунок bmp или в формате EMF.
Имеется очень удобная и подробная помощь, к сожалению, написанная по-английски. Программа адаптирована под Windows-95/98/Me/NT/2000/XP, применяются аналогичные панели инструментов, поэтому с ней очень удобно работать. По сравнению с широко известной программой «MathCad» обсуждаемая «Agrafer» отличается очень удобным интерфейсом, доступностью и простотой работы, не говоря уже о возможностях оформления графиков. Ученики могут освоить приемы работы с ней за один-два урока.
В старшей школе ученики часто сталкиваются с трудностями при построении графиков и анализе различных функциональных зависимостей. Данная программа может сделать этот процесс более интересным и эффективным, попутно способствуя расширению знаний и в информатике. Ее можно использовать при объяснении нового материала, для демонстрации графических зависимостей, а также для сравнения результатов анализа и построения некоторых графиков при обычном подходе и с использованием современных, компьютерных методов.
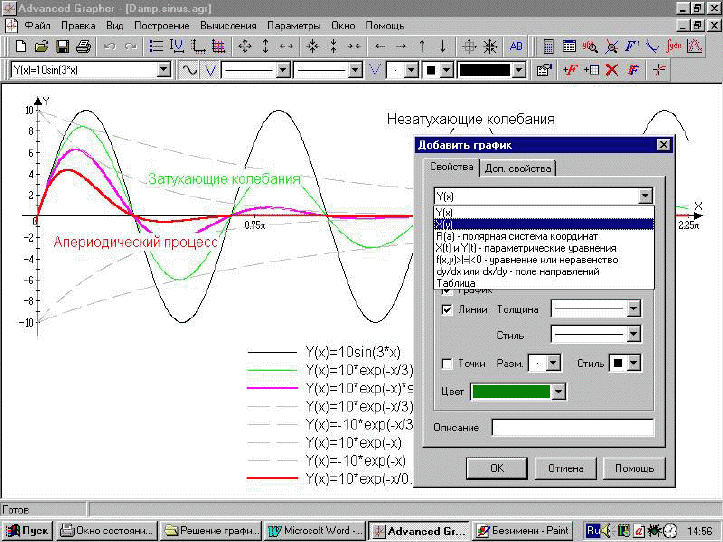
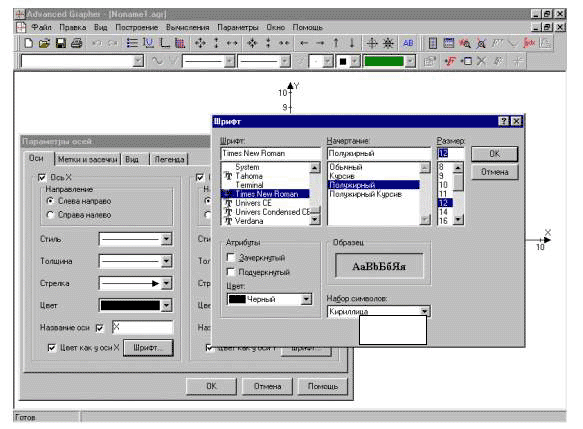
С чего начать при работе с программой? Нажимаем кнопку «Пуск», отыскиваем программу «Agrafer». После вызова программы появляется окно с панелью управления. После выбора типа координат, масштаба засечек на осях и т.д., приступаем к введению функции. Нажимаем «F+», при этом поверх основного окна появляется окно «Добавить график», куда и вводится функциональная зависимость (рис. 1). Вызвав окно «Параметры осей» (рис. 2), можно провести дальнейшее оформление графика, записать заголовок, привести легенду, определить тип линий и т.д. Вставка надписей на самом графике осуществляется путем нажатия на клавишу «АВ» на панели инструментов. Кстати, назначение той или иной клавиши появляется на подсказке, возникающей при подведении курсора «мыши» к клавише. Иногда удобно сделать координатную сетку. Надо стараться, чтобы школьники научились использовать все возможности программы для оформления графиков.

Основные начальные трудности при работе с программой и связанные с этим ошибки вызваны неправильной записью функций, поэтому мы приводим в тексте примеры полной формы записи выражения функции, необходимой для подстановки в программу. Приведем принятые сокращения при записи некоторых функций: sin – синус, соs – косинус, tan – тангенс, cot – котангенс, atan – обратный тангенс, asin – обратный синус, acos – обратный косинус, abs – абсолютное значение (модуль), sqrt – квадратный корень, ln – натуральный логарифм, lg – десятичный логарифм, exp – экспонента (exp(x); e^x).
Математические операции: (+, -) – сложение, вычитание, (*, /) – умножение, деление, (^) – возведение в степень.
Число p = 3,14… может быть
представлено либо символом Pi, либо, естественно,
числом. Последовательность выполнения операций,
выделение аргументов производятся только
круглыми скобками. Например: ln(ln(1/x)). Другие виды
скобок программа не воспринимает. Рассмотрим
применение данной программы для решения ряда
задач из курса физики старшей школы.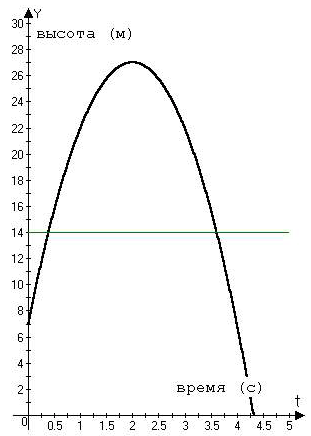
Пример. Тело брошено вверх со скоростью 20 м/с с высоты 7 м. Когда тело окажется на высоте 14 м? упадет на Землю? Когда тело окажется на максимальной высоте и чему она равна?
Запишем уравнение движения тела (ось y направлена вверх): y = y0 + v0 t – g t2/2.
Подставим числовые значения: y = 7 + 20t – 5t2.
Для программы это выражение надо записать так*:
Y = 7+20*X-5*X^2.
График, построенный с помощью программы «Аgrafer», представлен на рис. 3. Легко найти точки пересечения и экстремумы функции. Например, точки пересечения с функцией при Y = 14: X1 = 0.39,X2 = 3.61. Таким образом, тело окажется на высоте 14 м при движении вверх в момент t1 = 0,39 c, а при падении – в момент t2 = 3,61 с. Найдем теперь максимум функции, «нажав» на кнопки панели инструментов «Исследование функции», «Экстремумы» и «Нули функции». Получаем, что максимальная высота полета 27 м достигается при t = 2,00 с. Тело упадет на Землю при t = 4,32 c.
Пример. Пользуясь данными предыдущей задачи, отобразите изменения кинетической, потенциальной и полной механической энергий тела массой 1 кг.
Поскольку Ек = mv2/2, то можно записать: Ек = m/2 • (v0 – gt)2.
В данной задаче Ек = 0,5(20 – 10 t)2. В программу мы введем эту функцию в виде: y=0,5*(2-10*X)^2. Полученная кривая представлена на рис. 4.
Аналогично для потенциальной энергии (за начало отсчета принята поверхность Земли):
Еп = mgh = mgy = mg(y0 + v0t – gt2/2).
Подставляем числовые данные:
Еп = 10 • (7 + 20t – 5t2).
Для программы функцию представляем в виде:
Y = 10*(7+20*X-5X^2). График функции представлен на рис. 4.
Полную механическую энергию получим, сложив обе функции. Как следует из рис. 4, полная механическая энергия в течение всего полета, согласно закону сохранения энергии, не меняется. Максимум потенциальной энергии достигается при t = 2 c, т.е. в верхней точке полета, при этом кинетическая энергия обращается в 0.
Запишем стандартные уравнения для проекций скорости тела на оси координат:
vx = v0 • cos a; (1)
vy = v0 sin a – gt; (2)
х = v0 t cos a; (3)
y = h + v0 t sin a – gt2/2. (4)
Из (3) получим 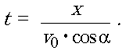 После подстановки этого значения в (4) получим
уравнение, описывающее траекторию движения тела:
После подстановки этого значения в (4) получим
уравнение, описывающее траекторию движения тела:
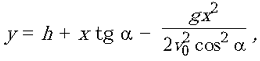 где h –
начальная высота бросания, a – угол бросания, v0 –
модуль вектора начальной скорости. Как видно, это
уравнение параболы. Построим графики с помощью
«Agrаfer» для трех стандартных значений угла a (30°;
45°; 60°), положив для простоты h = 0, v0 = 20
м/с, g = 9,8 м/с2.
где h –
начальная высота бросания, a – угол бросания, v0 –
модуль вектора начальной скорости. Как видно, это
уравнение параболы. Построим графики с помощью
«Agrаfer» для трех стандартных значений угла a (30°;
45°; 60°), положив для простоты h = 0, v0 = 20
м/с, g = 9,8 м/с2.
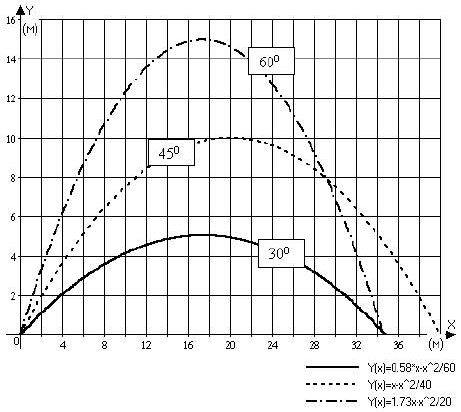
Вводим функции типа: Y=Xtg30-9.8*X^2/2*20^2cos30^2.
Получившиеся графики даны на рис. 5. Интересно, что при угле бросания 45° максимальная высота подъема тела составляет 1/4 от дальности бросания, которая при этом угле максимальна, – этот результат получен еще Галилеем. Кроме того, тела брошенные под углами 30° и 60°, пролетают одно и то же расстояние.
Школьники привыкли, что ускорение свободного
падения – величина постоянная: g0 = 9,81 м/c2.
Однако эта величина зависит от высоты Н над
поверхностью Земли: 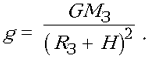 . Полезно построить график изменения
ускорения свободного падения от этой высоты.
Опять воспользуемся программой «Agrafer». Вводимая
функция у = a/(b + х)2 после подстановки
числовых значений имеет вид:
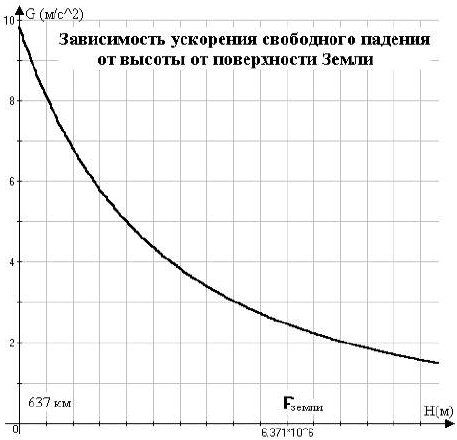
Y=6.67*10^(-11)*5.98*10^24/(6.371*10^6+X)^2. График приведен на рис. 6.
Одно деление по оси x (H) cоответствует 637,1 км (0,1RЗ).
Видно, что на высоте, равной радиусу Земли, g = (1/4)g0,
что легко видно из начальной формулы. Для задач,
обычно решаемых школьниками, действительно g»g0.
. Полезно построить график изменения
ускорения свободного падения от этой высоты.
Опять воспользуемся программой «Agrafer». Вводимая
функция у = a/(b + х)2 после подстановки
числовых значений имеет вид:
Y=6.67*10^(-11)*5.98*10^24/(6.371*10^6+X)^2. График приведен на рис. 6.
Одно деление по оси x (H) cоответствует 637,1 км (0,1RЗ).
Видно, что на высоте, равной радиусу Земли, g = (1/4)g0,
что легко видно из начальной формулы. Для задач,
обычно решаемых школьниками, действительно g»g0.
Зависимость средней квадратичной скорости
молекул от температуры описывается формулой 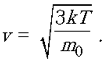 Хорошо
соответствуют модели идеального газа
одноатомные благородные газы, например Ar и He.
Массы атомов можно взять из справочника [1] либо
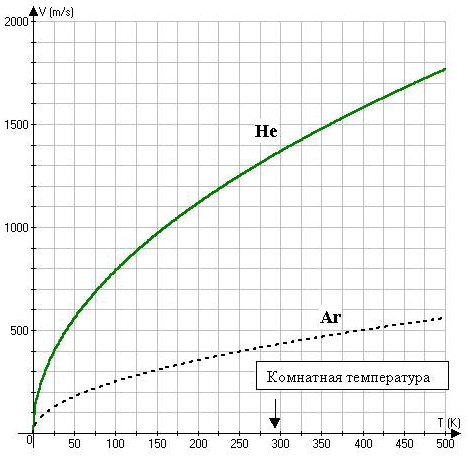
определить самостоятельно. На рис. 7 приведен
результат построения с помощью программы «Agrafer»
(Y1(X)=79*sqrt(X); Y2(X)=25*sqrt(X)). Видно, что при
одинаковой температуре скорости атомов Не
гораздо больше, чем более массивных атомов Ar.
Хорошо
соответствуют модели идеального газа
одноатомные благородные газы, например Ar и He.
Массы атомов можно взять из справочника [1] либо
определить самостоятельно. На рис. 7 приведен
результат построения с помощью программы «Agrafer»
(Y1(X)=79*sqrt(X); Y2(X)=25*sqrt(X)). Видно, что при
одинаковой температуре скорости атомов Не
гораздо больше, чем более массивных атомов Ar.
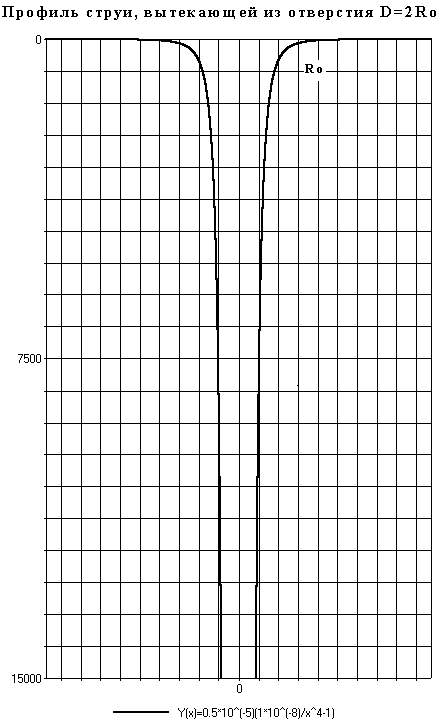 свободно и неразрывно вытекающей
вертикально вниз из отверстия радиусом R0 с
начальной скоростью v0
свободно и неразрывно вытекающей
вертикально вниз из отверстия радиусом R0 с
начальной скоростью v0
Из условия неразрывности и несжимаемости струи следует, что vS=const, где S=px2 – площадь струи. Связь между координатой у любой частицы струи и ее скоростью определяется зависимостью у = (v2 –v02 )/(2g).
Поскольку vS=v0S0, то выражение для
скорости можно представить в виде v=v0R02
/x2. Подставляя это выражение в уравнение
для у, получим: 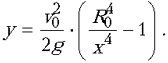
Построение графика лучше «поручить» программе «Agrafer», задав какие-либо разумные начальные числовые значения (рис. 8).
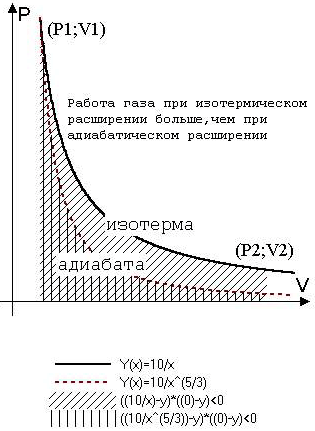
Идеальный газ начальным давлением p1, занимающий объем V1, расширяется до объема V2. В каком случае газ совершает бо1льшую работу – при изотермическом или при адиабатном расширении?
График изотермического процесса pV=const – гипербола (рис. 9). Работу, которую совершает газ, определяют по площади под графиком (математически находят значение определенного интеграла при изменении аргумента от V1 до V2). График гиперболы школьники могут легко построить сами. Сложнее с графиком адиабаты, соответствующем зависимости pVg=const, где g=Cp/CV=i+ 2/i (i – число степеней свободы). Для идеального газа (одноатомного) i=3, т.е. g=5/3=1,67. Поэтому функция имеет вид pV1,67=const. Поскольку начальные условия одинаковы (p1; V1), то графики исходят из одной точки.
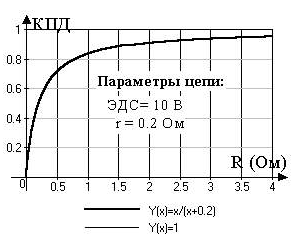
постройте графики зависимости КПД (h) источника и полезной мощности от сопротивления нагрузки (R). ЭДС и внутреннее сопротивление (r) источника тока заданы.
Поскольку полезная мощность Pпол = I2 • R, а затраченная Pзатр = I2 (R + r), то h=R/(R + r) (рис. 10). Видно, что h увеличивается с ростом R, всегда оставаясь меньше 1. Когда нагрузка равна внутреннему сопротивлению источника тока (0,2 Ом), h=0,5.
Теперь получим зависимость для полезной
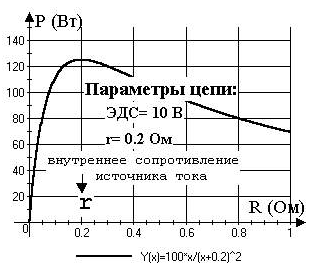
мощности. Поскольку ![]() Построим эту зависимость при
Построим эту зависимость при ![]() (pис. 11). Видно, что
максимальная мощность достигается при R=r, при
этом (см. рис. 10) h=0,5. Этот режим
используется, например, при работе
автомобильного стартера: половина энергии
аккумуляторной батареи теряется на ее нагрев.
(pис. 11). Видно, что
максимальная мощность достигается при R=r, при
этом (см. рис. 10) h=0,5. Этот режим
используется, например, при работе
автомобильного стартера: половина энергии
аккумуляторной батареи теряется на ее нагрев.
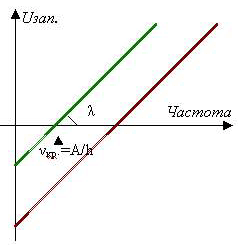
Стандартная задача: построить график зависимости запирающего напряжения от частоты падающего света.
Уравнение Эйнштейна: hn = A + eUзап=A + mv2/2.
Отсюда ![]() . Легко
построить график этой линейной зависимости. Для
катода с большим значением работы выхода график
пойдет правее. Интересно, что угол наклона при
этом не изменится, т.к.
. Легко
построить график этой линейной зависимости. Для
катода с большим значением работы выхода график
пойдет правее. Интересно, что угол наклона при
этом не изменится, т.к. ![]() (рис. 12).
(рис. 12).
А как выглядит график Uзап (l)?
Поскольку ln=c, то 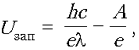 т.е. зависимость –
смещенная гипербола. Построим графики для двух
значений А (рис. 13).
т.е. зависимость –
смещенная гипербола. Построим графики для двух
значений А (рис. 13).
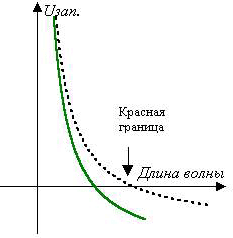
Кривая пересекает ось абсцисс в точке, соответствующей «красной границе» фотоэффекта для данного фотокатода. Для света большей длины волны фотоэффекта нет. «Красная граница» для катода с меньшей работой выхода сдвинута в сторону бо1льших длин волн.
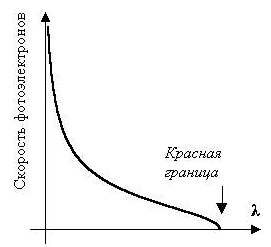 Сложнее построить график зависимости
скорости фотоэлектронов от длины волны
падающего света: поскольку
Сложнее построить график зависимости
скорости фотоэлектронов от длины волны
падающего света: поскольку
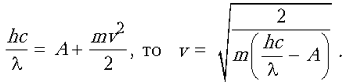
Программа «Agrafer» легко справляется с этой задачей (рис. 14).
При аварии на Чернобыльской АЭС людям, попавшим в зону радиоактивного заражения, в качестве профилактики прописывались препараты, содержащие йод. Причем такая профилактика была необходима именно в первые дни аварии. С чем это связано?
Среди продуктов радиоактивного заражения был и изотоп обычного йода – радиоактивный йод-131. Не забудем, что в обычном состоянии йод находится в виде молекулы I2 или солей типа KI, впрочем, это ничего не меняет в нашем рассмотрении.
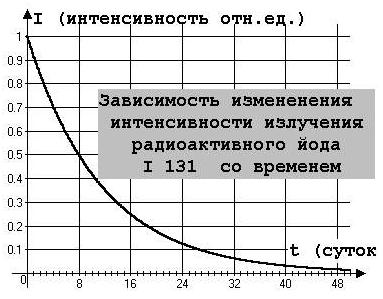
Щитовидная железа человека активно поглощает йод, поэтому может с водой, пылью, пищей получить изотоп йода, что приведет к радиоактивному воздействию на организм. Йодная профилактика состоит в насыщении щитовидной железы нормальным, нерадиоактивным йодом. Изменение со временем активности излучения изотопа йод-131 можно исследовать по графику I(t). Интенсивность I излучения пропорциональна количеству атомов изотопа. Воспользуемся законом распада: N=N0 • 2–t/T, где Т – период полураспада (8 суток для йода-131).
Отсюда I = I0 • 2–t/T. С помощью программы «Agrafer» строим график функции Y = 2^(-X/8), положив начальную интенсивность равной 1 (рис. 15). Видно, что спустя 8 суток интенсивность падает вдвое (результат очевидный), а спустя месяц интенсивность радиоактивного излучения уменьшается более чем на порядок.
Задача об определении длины тормозного пути подробно рассмотрена в № 35/02, с. 1 (В.Н.Томашов. Физика остановки автомобиля).
1. Енохович А.С. Справочник по физике. – М.: Просвещение, 1990.
2. Физика-10. /Под ред. Пинского А.А. – М.: Просвещение, 1999.
3. Орлов В.А. Школьный курс физики: тесты и задания. – М.: Школа-Пресс, 1996.
* Примечание. В программу вводятся только переменные X и Y, а оформление графика возможно с любыми переменными и подписями.
см. «Физика» № 45/02, с.10