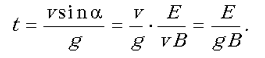
Задача 3
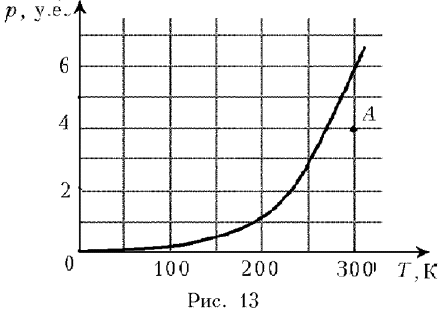
На рис. 13 приведен график зависимости давления насыщенного пара некоторого вещества от температуры. Определенное количество этого вещества находится в закрытом сосуде постоянного объема в равновесном состоянии, соответствующем точке A на рисунке. До какой температуры следует охладить эту систему, чтобы половина имеющегося в сосуде вещества сконденсировалась? Объемом сконденсировавшегося вещества можно пренебречь по сравнению с объемом сосуда.

Решение
Поскольку давление в точке A меньше давления насыщенных паров при температуре TA = 300 K, то все вещество находится в газообразном состоянии. Если бы вещество не конденсировалось, то давление p и температура T этого вещества в соответствии с уравнением Менделеева–Клапейрона были бы связаны прямо пропорциональной зависимостью p = bT. В условиях, когда вещество из пара переходит в конденсированное состояние, линейная зависимость давления от температуры при понижении температуры справедлива только до момента начала конденсации, который соответствует точке пересечения графика, приведенного на рисунке, с прямой линией p = bT, проходящей через начало координат и точку A.
Если, как это требуется по условию задачи, сконденсировалась половина имеющегося вещества, то это состояние будет соответствовать некоторой точке B на кривой зависимости давления насыщенного пара от температуры. Эту точку можно найти путем следующих рассуждений. Если все сконденсировавшееся вещество удалить, то давление в системе останется равным давлению насыщенного пара в точке B. Если теперь нагревать оставшийся пар до начальной температуры TA = 300 K, то его давление, очевидно, будет линейно возрастать до величины вдвое меньшей, чем было начальное давление pн, поскольку количество вещества в системе уменьшилось вдвое. Отсюда следует графический способ нахождения температуры, соответствующей точке B. Поставим на p,T-диаграмме (рис. 14) вспомогательную точку C, соответствующую начальной температуре TA = 300 K и давлению, вдвое меньшему начального.
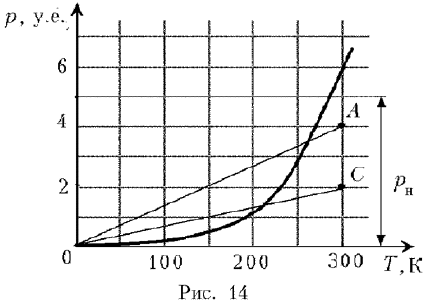
Проведем через точку C и начало координат прямую линию. Эта линия пересечет график зависимости давления насыщенного пара от температуры в искомой точке B, соответствующей в нашем случае температуре T » 200 K.
Задача 4
Маленький шарик массой m и зарядом q, брошенный со скоростью v под углом a = 45° к горизонту, пролетев вдоль поверхности Земли расстояние L, попадает в область пространства, в которой, кроме поля силы тяжести, имеется еще и однородное постоянное горизонтальное электрическое поле. Граница этой области вертикальна. Через некоторое время после этого шарик падает в точку, откуда был произведен бросок. Найти напряженность электрического поля E. Ускорение свободного падения равно g, влиянием воздуха пренебречь.
Решение
Ясно, что для выполнения условий задачи шарик после попадания в поле должен выталкиваться из него, в противном случае он никогда не покинет область поля и, следовательно, не сможет вернуться в исходную точку. Предположим далее, что плоскость траектории шарика до его попадания в поле перпендикулярна границе области, в которой имеется поле. Тогда для выполнения условий задачи необходимо, как минимум, чтобы силовые линии поля были также перпендикулярны границе указанной области. Действительно, если бы силовые линии были направлены под углом к границе области, в которой имеется поле, то шарик за время движения в поле приобрел бы «боковую» составляющую скорости, направленную вдоль этой границы (перпендикулярно плоскости начальной траектории), и не смог бы вернуться в исходную точку. Пусть теперь плоскость траектории шарика до его попадания в поле составляет с границей области, в которой имеется поле, некоторый угол. Тогда, очевидно, для выполнения условий задачи необходимо, как минимум, чтобы силовые линии поля составляли с границей области поля точно такой же угол, в противном случае у шарика опять же появится «боковая» составляющая скорости, перпендикулярная плоскости начальной траектории, и шарик не сможет упасть в исходную точку. Таким образом, мы доказали, что в любом случае траектория шарика как до, так и после его попадания в поле лежит в вертикальной плоскости, параллельной силовым линиям поля. При этом данная плоскость может составлять некоторый угол с границей области, в которой имеется поле.
Теперь выясним, каким образом должен двигаться шарик в электрическом поле. Разложим вектор скорости шарика в момент его попадания в поле на две составляющие: горизонтальную, параллельную силовым линиям, и вертикальную. Так как электрическое поле потенциально, то горизонтальная составляющая скорости шарика при его вылете из поля сохранит величину и изменит знак по сравнению с горизонтальной составляющей в момент попадания шарика в поле. Значит, время, проходящее от момента броска шарика до его попадания в поле, равно времени, проходящему от момента вылета шарика из поля до его падения, и равно отношению расстояния L к величине горизонтальной составляющей скорости. С другой стороны, это время равно времени подъема шарика в поле тяжести от места броска до уровня точки пересечения границы поля, а также времени движения от данной точки до точки падения. В силу потенциальности поля тяжести вертикальная составляющая скорости шарика при его движении вверх и вниз на одной и той же высоте одинакова, а с ростом высоты уменьшается. Поэтому, если бы шарик вылетел из поля выше точки его попадания в поле, то время движения вниз до точки падения было бы больше, а если ниже, то меньше упомянутого выше времени подъема шарика от точки броска до точки его попадания в поле. Следовательно, для того чтобы шарик упал в исходную точку, необходимо, чтобы вертикальная составляющая скорости шарика за время его нахождения в поле также изменила знак и сохранила свою величину, причем точки попадания шарика в поле и его вылета из поля должны совпадать. Это возможно только в том случае, когда шарик в поле движется по прямой линии, вдоль которой направлен вектор действующей на шарик суммарной силы mg + qE.
Итак, мы доказали следующие утверждения. Для того чтобы шарик мог вернуться в исходную точку, необходимо, чтобы он после вылета из электрического поля двигался назад по той же траектории, по которой он летел от момента броска до попадания в электрическое поле. Это возможно лишь в том случае, если траектория шарика все время лежит в плоскости, параллельной силовым линиям электрического поля, причем они должны быть направлены так, чтобы выталкивать шарик из поля.
Для дальнейшего решения задачи введем прямоугольную систему координат с началом в точке броска шарика, поместим ее в плоскость траектории шарика и направим координатную ось x вдоль поверхности Земли (антипараллельно линиям электрического поля), а ось y – вверх. Пусть шарик влетает в электрическое поле, имея проекции скорости vx и vy. При вылете из поля проекции скорости, как мы уже выяснили, должны остаться прежними по величине и изменить свой знак. Так как шарик движется в поле вдоль оси x с постоянным ускорением, а вдоль оси y – с ускорением свободного падения –g, то для проекций его скорости в момент вылета из поля можно записать:
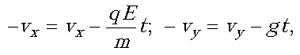
где t – время полета шарика в электрическом поле. Из этих соотношений получаем:
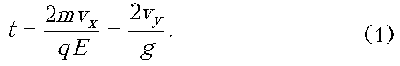
Пусть от момента броска шарика до его попадания в электрическое поле прошло время t. Тогда из уравнений кинематики получаем:
![]()
Исключая из двух последних уравнений t, получаем выражение для проекции скорости vy:
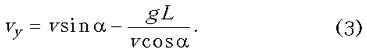
Подставляя (2) и (3) в (1) и учитывая, что a = 45°, находим напряженность поля E:
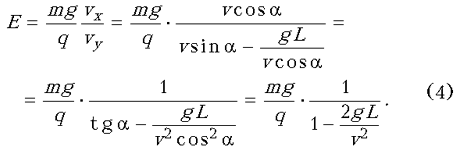
Из этого выражения видно, что решение задачи
существует при условии ![]() Данное условие означает, что шарик
должен влетать в электрическое поле прежде, чем
достигнет наивысшей точки своей траектории при
полете вне поля. Из формулы (4), кроме того,
следует, что при движении, удовлетворяющем
условиям задачи, справедливо соотношение
Данное условие означает, что шарик
должен влетать в электрическое поле прежде, чем
достигнет наивысшей точки своей траектории при
полете вне поля. Из формулы (4), кроме того,
следует, что при движении, удовлетворяющем
условиям задачи, справедливо соотношение
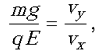
которое и означает, что в момент попадания шарика в электрическое поле его скорость направлена вдоль суммарной силы, действующей на шарик в электрическом поле и поле силы тяжести. Следовательно, шарик движется в поле с ускорением вдоль прямой, составляющей с горизонталью угол
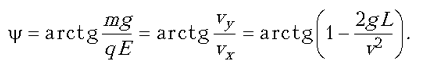
Следует отметить, что в общем случае движение заряженного шарика во взаимно перпендикулярных однородных гравитационном и электрическом полях происходит по параболе, которая в данном случае вырождается в прямую.
Задачу можно решать и «в лоб», последовательно рассматривая движение шарика до попадания в поле, его полет в поле и движение после вылета из поля. Однако этот способ решения достаточно громоздок.
Задача 5
В «черном ящике» с двумя контактами находится
схема, состоящая из незаряженного конденсатора и
резистора. К контактам в момент времени t = 0
подсоединили конденсатор емкостью C, имеющий
заряд Q0. График зависимости 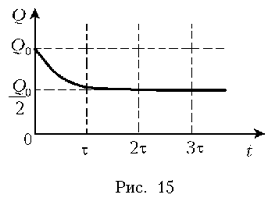 заряда на этом
конденсаторе от времени изображен на рис. 15.
Найти сопротивление резистора и емкость
конденсатора, находящихся в «черном ящике».
заряда на этом
конденсаторе от времени изображен на рис. 15.
Найти сопротивление резистора и емкость
конденсатора, находящихся в «черном ящике».
Решение
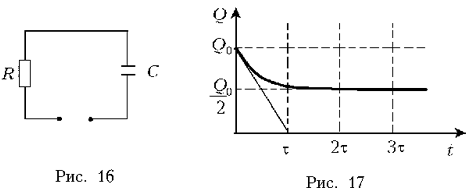
Так как конденсатор разряжается не до конца, то в «черном ящике» может находиться только схема, изображенная на рис. 16. Поскольку установившийся заряд на конденсаторе C равен Q0/2, то емкость конденсатора C1 в «черном ящике» также равна C.
В начальный момент времени ток через резистор в
соответствии с определением силы тока равен , где
DQ – заряд, стекший с конденсатора
за малое время Dt, прошедшее после
начала его разрядки. Отношение равно угловому
коэффициенту касательной к графику, проведенной
в точке, соответствующей моменту времени
t = 0 (рис. 17). Из графика видно, что эта
касательная, выходящая из точки Q0 на оси
ординат, отсекает на оси абсцисс отрезок времени,
равный t. Таким образом, начальный ток через
резистор равен ![]() а
падение напряжения на нем
а
падение напряжения на нем ![]() . Поэтому сопротивление резистора
. Поэтому сопротивление резистора
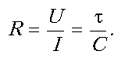
11-й класс
Задача 1
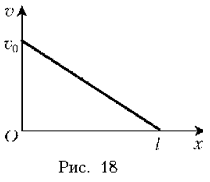 Телу
массой m, находящемуся на горизонтальной
поверхности, сообщили скорость v0 в направлении
оси Ox. График зависимости скорости тела v от его
координаты x изображен на рис. 18. Найти
зависимость величины силы трения, действующей на
тело, от координаты х.
Телу
массой m, находящемуся на горизонтальной
поверхности, сообщили скорость v0 в направлении
оси Ox. График зависимости скорости тела v от его
координаты x изображен на рис. 18. Найти
зависимость величины силы трения, действующей на
тело, от координаты х.
Решение
Работа, совершенная силой трения к моменту попадания тела в точку с координатой х, по модулю равна
Следовательно, на участке от x до x + Dx совершается работа
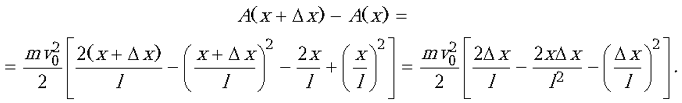
При малых Dx последним слагаемым можно пренебречь. Поскольку A(x + Dx) – A(x) = Fтр • Dx, то для силы трения, действующей на тело в точке x, получаем:
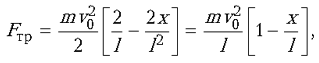
т.е. сила трения линейно зависит от координаты x.
Задачу можно решать и другим, более формальным способом. Действительно, искомая величина силы трения в соответствии со вторым законом Ньютона равна Fтр = |ma|. По определению ускорения имеем
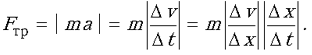
Но 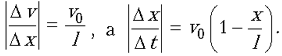 Отсюда для
величины силы трения получаем прежний ответ.
Отсюда для
величины силы трения получаем прежний ответ.
Задача 2
Два закрытых сосуда емкостью V1 = 10 л и V2 = 20 л имеют жесткие стенки и поддерживаются при одинаковой постоянной температуре 0 °C. Сосуды соединены короткой трубкой с краном. Вначале кран закрыт. В первом сосуде находится воздух под давлением p1 = 2 атм при относительной влажности r1 = 20%. Во втором сосуде находится воздух под давлением p2 = 1 атм при относительной влажности r2 = 40%. Кран постепенно открыва-ют так, что процесс выравнивания давлений в сосудах можно считать изотермическим. Найти минимальную и максимальную относительную влажность воздуха в сосуде емкостью 10 л.
Решение
При указанной температуре, а ее, по условию
задачи, поддерживают постоянной, давление
насыщенных паров воды pн много меньше, чем
атмосферное давление, поэтому массой молекул
воды можно пренебречь по сравнению с массой
других газов, составляющих воздух. Масса газа в
каждом сосуде пропорциональна произведению
давления и объема (в соответствии с уравнением
Клапейрона–Менделеева). До открывания крана в
обоих сосудах масса газа была одинакова и
пропорциональна произведению ![]() . После открывания крана в
сосудах достаточно быстро установится
одинаковое давление. Суммарный объем равен
теперь 30 л, суммарная масса пропорциональна
. После открывания крана в
сосудах достаточно быстро установится
одинаковое давление. Суммарный объем равен
теперь 30 л, суммарная масса пропорциональна ![]() в
соответствии с законом Бойля–Мариотта. Отсюда
установившееся давление равно
в
соответствии с законом Бойля–Мариотта. Отсюда
установившееся давление равно 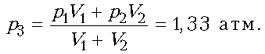 При этом из десятилитрового
сосуда в двадцатилитровый сосуд перейдет часть
содержимого. Давление при постоянной
температуре пропорционально концентрации
молекул. Концентрация молекул в сосуде объемом 20
л уменьшилась в
При этом из десятилитрового
сосуда в двадцатилитровый сосуд перейдет часть
содержимого. Давление при постоянной
температуре пропорционально концентрации
молекул. Концентрация молекул в сосуде объемом 20
л уменьшилась в 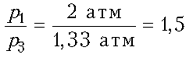 раза. Вместе с молекулами кислорода и азота, из
которых в основном состоит воздух, из сосуда
объемом 10 л в сосуд объемом 20 л при быстром
установлении давления перебрались и молекулы
воды, поэтому их концентрация тоже уменьшилась
во столько же раз. Относительная влажность
воздуха r = р/рн при постоянной температуре
пропорциональна концентрации молекул воды.
Поэтому в малом сосу- де влажность вначале
уменьшится до величины
раза. Вместе с молекулами кислорода и азота, из
которых в основном состоит воздух, из сосуда
объемом 10 л в сосуд объемом 20 л при быстром
установлении давления перебрались и молекулы
воды, поэтому их концентрация тоже уменьшилась
во столько же раз. Относительная влажность
воздуха r = р/рн при постоянной температуре
пропорциональна концентрации молекул воды.
Поэтому в малом сосу- де влажность вначале
уменьшится до величины
![]()
Со временем в результате диффузии в обоих
сосудах установится одинаковая концентрация
молекул воды. До открывания крана общее
количество молекул воды было пропорционально
величине ![]() После
установления равновесного распределения
молекул воды их общее количество останется тем
же и будет пропорционально
После
установления равновесного распределения
молекул воды их общее количество останется тем
же и будет пропорционально ![]() Величина r3 и будет новой
относительной влажностью воздуха в сосуде
объемом 10 л:
Величина r3 и будет новой
относительной влажностью воздуха в сосуде
объемом 10 л:
![]()
Отсюда
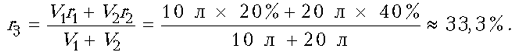
Таким образом, после открывания крана
относительная влажность воздуха в меньшем
сосуде вначале, при выравнивании давлений в
сосудах, уменьшится от r1= 20% до 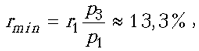 , а затем, во время
процесса диффузии, возрастет до
максимального значения
, а затем, во время
процесса диффузии, возрастет до
максимального значения 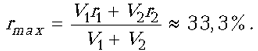
Задача 3
Заряженная частица двигалась в некоторой области пространства, где имеются взаимно перпендикулярные однородные поля: электрическое – с напряженностью E, магнитное – с индукцией B и поле силы тяжести g. Вектор скорости частицы при этом был постоянным и перпендикулярным магнитному полю. После того как частица покинула эту область пространства и начала движение в другой области, где имеется только поле силы тяжести g, ее скорость начала уменьшаться. Через какое время после вылета частицы из первой области ее скорость достигнет минимального значения?
Решение
 После
того как частица начала двигаться в области
пространства, где есть только поле g, ее скорость
начала уменьшаться. Это означает, что скорость
частицы имеет составляющую, направленную
противоположно вектору g, т.е. движется «вверх» по
отношению к полю силы тяжести. Следовательно,
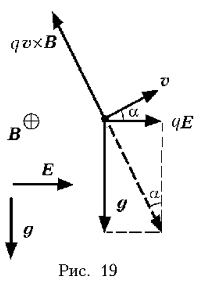
векторы E, B, g, скорость частицы v и действующие на
нее электрическая, магнитная и гравитационная
силы направлены так, как показано на рис. 19. Угол к
горизонту, под которым частица двигалась,
находясь во всех трех полях, может быть найден из
условия равенства нулю суммы действующих на нее
сил:
После
того как частица начала двигаться в области
пространства, где есть только поле g, ее скорость
начала уменьшаться. Это означает, что скорость
частицы имеет составляющую, направленную
противоположно вектору g, т.е. движется «вверх» по
отношению к полю силы тяжести. Следовательно,
векторы E, B, g, скорость частицы v и действующие на
нее электрическая, магнитная и гравитационная
силы направлены так, как показано на рис. 19. Угол к
горизонту, под которым частица двигалась,
находясь во всех трех полях, может быть найден из
условия равенства нулю суммы действующих на нее
сил:
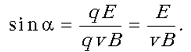
После попадания в область пространства, где
есть только поле силы тяжести, частица будет
двигаться по параболе. Ее скорость будет
минимальна в верхней точке траектории, тогда,
когда вертикальная составляющая скорости
обратится в нуль. Это произойдет через время