Абитуриенту

С.С. Чесноков, С.Ю. Никитин,
И.П. Николаев, Н.Б. Подымова,
М.С. Полякова, проф. В.И. Шмальгаузен,
физфак МГУ, г. Москва

Продолжение. См. № 6/2002

Хочу учиться на ВМК!

Задачи, предлагавшиеся на вступительных экзаменах
на факультет вычислительной математики и кибернетики
МГУ им. М.В. Ломоносова в 2001 г.

I. Механика

• Начальный участок трассы скоростного спуска, расположенный вниз по склону горы с углом наклона a = 45° к горизонту, горнолыжник прошел, не отталкиваясь палками. Какую максимальную скорость vmax мог развить спортсмен на этом участке, если его масса m = 70 кг? Коэффициент трения лыж о снег m = 0,1, сила сопротивления воздуха пропорциональна квадрату скорости: F = bv², где постоянный коэффициент b = 0,9 кг/м. Ускорение свободного падения принять g = 10 м/с².

Решение

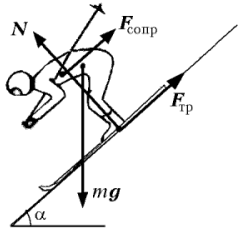
Горнолыжник, скатывающийся по наклонному участку трассы, находится под действием сил, изображенных на рисунке, где mg – сила тяжести, N – нормальная составляющая силы реакции склона, F_тр – сила трения лыж о снег, F_сопр – сила сопротивления воздуха. Поскольку, по условию задачи, лыжник движется поступательно, его можно принять за материальную точку и считать, что точки приложения всех перечисленных сил совпадают.

В проекции на координатную ось, направленную вниз по склону, уравнение движения лыжника имеет вид:

где a – ускорение лыжника, F_тр=mN = mmg cosa, F_cопр= bv². Ясно, что при движении под действием двух постоянных сил (проекции силы тяжести и силы сухого трения) и зависящей от скорости силы сопротивления воздуха, ускорение лыжника по мере разгона уменьшается и при некоторой скорости обращается в нуль. Это и есть максимальная скорость лыжника на данном отрезке трассы, поскольку его дальнейшее движение будет равномерным. Таким образом, при установившемся движении лыжника

Отсюда после элементарных преобразований получаем ответ:

• Шарик бросают с башни высотой h = 4,9 м под углом a = 30° к горизонту со скоростью v₀ = 7 м/с. При падении на землю шарик упруго ударяется о наклонную плоскость и возвращается в точку бросания по той же траектории. Какой угол b составляет наклонная плоскость с горизонтом? Ускорение свободного падения g = 10 м/c²

Решение

Чтобы после упругого удара о наклонную плоскость шарик вернулся в точку бросания по той же траектории, что и при падении, 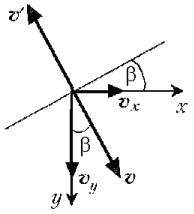нужно, чтобы плоскость была расположена перпендикулярно его скорости v непосредственно перед ударом. Поэтому угол b между наклонной плоскостью и горизонталью равен углу между скоростью шарика в момент падения v и вертикалью. Обозначив через v_x горизонтальную составляющую скорости шарика, получаем 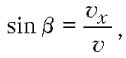причем v_x = v₀cosa. Для определения скорости тела при падении на наклонную плоскость воспользуемся законом сохранения энергии, согласно которому

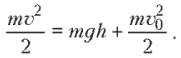  Отсюда  Объединяя записанные выражения, получаем ответ:

• На прямолинейном горизонтальном участке пути стоят N=5 одинаковых вагонов. Промежутки между соседними вагонами одинаковы и равны L = 30 м. К крайнему вагону подкатывается еще один такой же вагон, имеющий скорость v₀ = 2 м/с. В результате N последовательных столкновений, в каждом из которых сталкивающиеся вагоны сцепляются вместе, все N+1 вагонов соединяются в один состав. Найдите время t между первым и последним столкновениями. Силами сопротивления движению вагонов пренебречь.

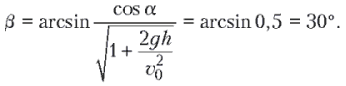
Решение

Поскольку силы сопротивления пренебрежимо малы, движущийся и покоящиеся вагоны представляют собой замкнутую механическую систему. Обозначив через m массу отдельного вагона, рассмотрим k их последовательных столкновений, в каждом из которых выполняется закон сохранения импульса:

где v_k – скорость состава после k-го столкновения. Из этих соотношений следует, что Поэтому время между k-м и (k+1)-м столкновениями равно .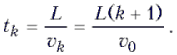

Искомое время между первым и последним, т.е. (N – 1)-м, столкновениями

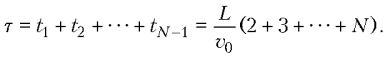
Применяя формулу для суммы арифметической прогрессии, находим ответ: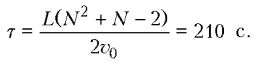

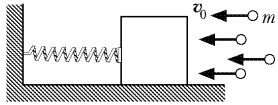
• Брусок расположен на гладкой горизонтальной плоскости и соединен горизонтальной пружиной жесткостью k = 100 Н/м с вертикальной стенкой. Перпендикулярно поверхности бруска летят капли воды массой m = 0,1 г каждая со скоростью v₀ = 5 м/с. Ударившись о брусок, капли, не отскакивая от него, стекают на землю. Найдите, на какую величину Dl сжимается пружина, если известно, что брусок не совершает колебаний. Число капель в единице объема потока n= 2 • 10³ м^-3. Площадь поверхности бруска, в которую ударяют капли, S = 100 см².

 Решение

Ударяющиеся о поверхность бруска капли воды оказывают на нее давление, подобно тому, как оказывают давление на стенку сосуда молекулы находящегося в нем газа. Поэтому для решения задачи можно воспользоваться приемами, применяемыми для вывода основного уравнения молекулярно-кинетической теории идеального газа, с той лишь разницей, что соударения капель с поверхностью бруска являются неупругими, и все капли в отличие от молекул газа летят с одной и той же скоростью.

Изменение импульса одной капли при ударе о поверхность неподвижного бруска Dp₁ = mv₀. За время Dt о брусок ударяется N=nSv₀Dt капель. Следовательно, импульс силы давления капель на поверхность бруска за время Dt равен: FDt = Np₁ = mnv₀²SDt, а величина самой силы давления есть F=mnv₀²S. Под действием этой силы брусок смещается на некоторое расстояние Dl, сжимая пружину. Возникающая в пружине сила упругости F_упр = kDl уравновешивает силу давления капель: F=F_упр. Объединяя записанные соотношения, получаем ответ: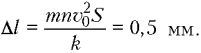

• Шарик массой m = 0,1 г, несущий отрицательный заряд q=–10^–7 Кл, движется по силовой линии однородного электрического поля напряженностью E=7 · 10³ В/м, направленной вертикально вниз. На пути l = 1 м скорость шарика изменилась по модулю в 2 раза, а направление скорости осталось неизменным. Найти скорость шарика v в конце этого пути. Ускорение свободного падения g = 10 м/с². Сопротивлением воздуха пренебречь.

Решение

Шарик движется под действием двух сил: силы тяжести и кулоновской силы, причем последняя направлена против электрического поля, поскольку заряд шарика отрицательный. В проекции на вертикальную координатную ось, направленную вниз, суммарная сила, действующая на шарик, равна

F = mg – |q|E.

При перемещении l эта сила совершает работу A = (mg – |q|E)l. По условию задачи, шарик движется по полю, т.е. вниз, и на рассматриваемом отрезке пути его скорость не меняет своего направления. Следовательно, перемещение шарика положительно. В соответствии с законом изменения кинетической энергии тела

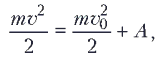
где v₀ – скорость шарика в начале рассматриваемого пути, v – его скорость в конце этого пути. Из последнего соотношения находим

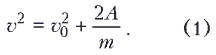
Очевидно, что ответ зависит от знака работы, который определяется знаком проекции суммарной силы, действующей на шарик, на выбранную координатную ось. Таким образом, если сила тяжести больше кулоновской силы, то F>A; A>0, и скорость шарика увеличивается в два раза (v = 2v₀), при этом равенство (1) принимает вид:

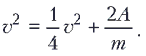
В противном случае A< 0, и скорость шарика уменьшается в два раза (v = v₀/2); тогда из (1) следует:

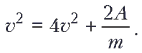
.Объединяя записанные соотношения, получаем ответ:

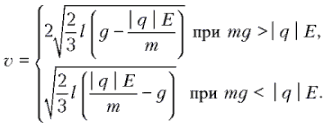
 Подстановка числовых данных из условия задачи дает для конечной скорости значение v»2,8 м/с.

.