Л.Л. Куликова (учитель математики),
Т.В. Ширяева (учитель физики),
школа № 23, г. Находка, Приморский край
Применение матанализа при решении физических задач
Открытый интегрированный урок : физика
+ математика.
10-й класс. Углубленный курс
Цель: научить применять методы математического анализа при решении физических задач; продолжить работу по ознакомлению учащихся с методами научного познания мира; выявить эмпирическую зависимость силы тока в полной цепи от внешнего сопротивления; закрепить навыки вычисления производной для нахождения физических величин и построения графиков; закрепить знания закономерностей соединения проводников, закона Ома для полной цепи, мощности тока; закрепить навыки составления электрических цепей, измерения силы тока, напряжения, ЭДС, расчета внутреннего сопротивления; продолжить обучение анализировать условие задачи, составлять планы решения задачи и проведения эксперимента; продолжить развитие навыков совместной работы в группе малого состава.
Оборудование: кодоскоп, экран; прибор Ионтеля, амперметр, вольтметр, источник тока на 6 В, соединительные провода; на столах учащихся – приборы Ионтеля, учебные амперметры, вольтметры, источники тока на 4,5 В, соединительные провода.
I. Организационный этап.
Постановка цели урока
Учитель математики. «Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон», – этими словами А.Попа [см., например, № 28/2000, с. 7, 8. – Ред.] мы хотим начать интегрированный урок физики и математики. На прошлом таком уроке мы говорили, что понятие производной возникло как математическое описание скорости движения. Через производную по времени координаты точки можно выразить механические величины (силу, импульс, кинетическую энергию), через производную магнитного потока – электрические величины (например ЭДС индукции), через производную заряда – силу тока и т.д. Сегодня мы продолжаем разговор о применении производной и использовании математического анализа для решения физических задач.
В начале урока в процессе игры «Поле чудес» мы проверим, как вы усвоили простейшие физические задачи, связанные с производной.
II. Проверка знаний
Учитель физики. Напоминаем правила игры:
– взять карточку, отметить ее номер у учителя, решить задачу, не забывая, что каждая физическая величина имеет единицу в системе СИ;
– по кодовой таблице найти букву, соответствующую ответу, и рядом с номером задачи итоговой таблицы на доске вписать ее. Должна получиться «крылатая» фраза римского философа Цицерона.
Самых активных участников игры ждут награды: за правильно решенные 3–4 задачи – «5», за правильно решенные 4 задачи на нахождение разных физических величин – приз, и первый, угадавший фразу, тоже получит приз.
Начало игры. Учитель записывает номера задач, выбираемых каждым учеником; на столах – кодовые таблицы, на доске – итоговая таблица, в левой строке которой – номера задач, в правую строку надо вписать буквы, из которых складывается фраза»: «Недостаточно обладать мудростью, надо уметь пользоваться ею».
Окончание игры. Награждение победителей, оценка активных игроков, подведение итогов.
Кодовая таблица

Задания «Поле чудес»
1. Тело движется прямолинейно по закону x(t) = 2t3 – 2,5t2 + 3t + 1 (х выражена в метрах, t – в секундах). Найти скорость тела при t = 1 с.
2. Тело движется прямолинейно по закону 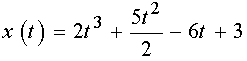 (х
выражена в метрах, t – в секундах). Найти
скорость при t = 1 с.
(х
выражена в метрах, t – в секундах). Найти
скорость при t = 1 с.
3. Заряд q изменяется по закону q(t) = 0,4t2 (q выражен в кулонах, t – в секундах). Найти силу тока при t = 10 с.
4. Угол поворота тела вокруг оси изменяется по закону j(t) = 0,3t2 – 0,5t + 0,4 (j – в радианах, t – в секундах). Найти угловую скорость при t = 10 с.
5. Определить скорость колеблющегося тела в момент t = 2 с, если координата изменяется по закону x(t) = 2 sin 2pt (х выражена в метрах, t – в секундах).
6. Определить ускорение колеблющегося тела
при t = 4 с, если его координата
изменяется по закону  (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
7. Тело массой 1 кг 200 г движется
прямолинейно по закону 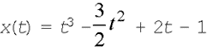 (х выражена в метрах, t
– в секундах). Найти импульс при t=3 с.
(х выражена в метрах, t
– в секундах). Найти импульс при t=3 с.
8. Определить ускорение колеблющегося тела
при t=6 с, если его координата
изменяется по закону 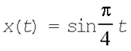 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
9. Заряд q изменяется по закону q(t) = t(0,25t – 1), причем (q выражен в кулонах, t – в секундах). Найти силу тока при t=13 с.
10. Тело массой 300 г движется прямолинейно по закону x(t) = 6t3 + 2t – 7 (х выражена в метрах, t – в секундах). Найти силу, действующую на это тело при t=3 c.
11. Тело движется прямолинейно по закону 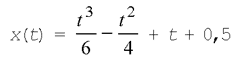 (х
выражена в метрах, t – в секундах). Найти
скорость при t=3 с.
(х
выражена в метрах, t – в секундах). Найти
скорость при t=3 с.
12. Температура тела T изменяется по
закону 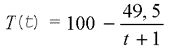 (Т
выражена в кельвинах, t – в секундах).
Какова скорость изменения температуры при t=2 с?
(Т
выражена в кельвинах, t – в секундах).
Какова скорость изменения температуры при t=2 с?
13. Температура тела T изменяется по
закону 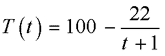 (Т
выражена в кельвинах, t – в секундах).
Какова скорость изменения температуры при t=1 с?
(Т
выражена в кельвинах, t – в секундах).
Какова скорость изменения температуры при t=1 с?
14. Тело массой 4,2 кг движется прямолинейно
по закону 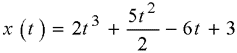 (х
выражена в метрах, t – в секундах). Найти
кинетическую энергию тела при t=1 с.
(х
выражена в метрах, t – в секундах). Найти
кинетическую энергию тела при t=1 с.
15. Температура тела T изменяется в
зависимости от времени по закону T(t) = 0,2t2
(Т выражена в кельвинах, t – в
секундах). Какова скорость изменения температуры
при ![]() ?
?
16. Тело массой 6 кг движется прямолинейно по закону x(t) = 2t3 –2,5t2 + 3t + 1 (х выражена в метрах, t – в секундах). Найти импульс тела при t=1 с.
17. Тело массой 2 кг движется прямолинейно по закону x(t) = (t – 5)(6 + 2t) + 50 (х выражена в метрах, t – в секундах). Найти силу при t=4 с.
18. Тело массой 1 кг 600 г движется
прямолинейно по закону 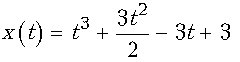 (х выражена в метрах, t
– в секундах). Найти импульс тела при t=2 c.
(х выражена в метрах, t
– в секундах). Найти импульс тела при t=2 c.
19. Определить ускорение колеблющегося тела
при t=2 с, если его координата
изменяется по закону 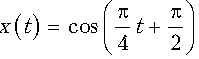 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
20. Угол поворота тела вокруг оси j(t) = 0,3t2 –0,4t + 7 (j выражен в радианах, t – в секундах). Найти угловую скорость при t=8с.
21. Из одного и того же порта вышли два парохода: один – на север, другой – на запад. С какой скоростью возрастает расстояние между ними, если скорость этих теплоходов 30 км/ч и 40 км/ч?
22. Из одного и того же порта вышли два парохода: один – на север, другой – на запад. С какой скоростью возрастает расстояние между ними, если скорость этих теплоходов 24 км/ч и 32 км/ч?
23. Температура тела T изменяется по закону T(t) = 0,5t2 – 2t (Т выражена в кельвинах, t – в секундах). Найти скорость изменения температуры при t=10 c.
24. Тело массой 200 г движется прямолинейно по закону x(t) = 6t3 + 2t – 7 (х выражена в метрах, t – в секундах). Найти силу, действующую на это тело в момент t=3 с.
25. Материальная точка движется по закону 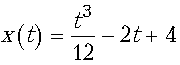 (х
выражена в метрах, t – в секундах). Найти
ускорение этой точки при t=11 с.
(х
выражена в метрах, t – в секундах). Найти
ускорение этой точки при t=11 с.
26. Определить скорость колеблющегося тела
при t=5 с, если его координата
изменяется по закону 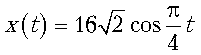 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
27. Определить ускорение колеблющегося тела
при t=2 с, если его координата
изменяется по закону 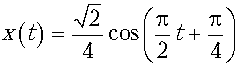 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
28. Угол поворота тела вокруг оси изменяется по закону j(t) = 0,4t2 – 2t + 1 (j выражен в радианах, t – в секундах). Найти угловую скорость при t=8 с.
29. Из одного и того же порта вышли два парохода: один – на север, другой – на запад. С какой скоростью возрастает расстояние между ними, если скорость этих теплоходов 22,5 км/ч и 30 км/ч?
30. Температура тела изменяется по закону T(t) = 0,2t2 + 0,12 (T выражена в кельвинах, t – в секундах). Какова скорость изменения температуры при t=10 с?
31. Тело массой 4 кг 800 г движется
прямолинейно по закону 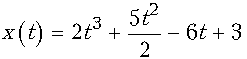 (х выражена в метрах, t
– в секундах). Найти импульс в момент t=1 с.
(х выражена в метрах, t
– в секундах). Найти импульс в момент t=1 с.
32. Угол поворота тела вокруг оси изменяется по закону j(t) = 1,5t2 – 0,1t (j выражен в радианах, t – в секундах). Найти угловую скорость в момент времени t=2,7 с.
33. Тело массой 5,5 кг движется прямолинейно по закону x(t) = (6 – t)(2t + 3) – 18 (х выражена в метрах, t – в секундах). Найти импульс тела при t=2 с.
34. Заряд q изменяется по закону q(t) = 3t2 + 4t (q выражен в кулонах, t – в секундах). Найти силу тока при t=6 с.
35. Тело массой 20 кг движется прямолинейно
по закону 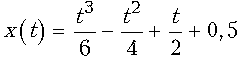 (х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=3 с.
(х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=3 с.
36. Тело массой 2 кг движется прямолинейно
по закону 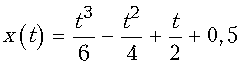 (х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=3 с.
(х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=3 с.
37. Определить ускорение колеблющегося тела в
момент t=1 с, если его координата
изменяется по закону 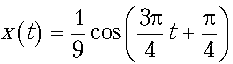 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
38. Заряд q изменяется по закону q(t) = 0,4t2 + 1,2t (q выражен в кулонах, t – в секундах). Найти силу тока при t=4 с.
39. Из одного и того же порта вышли два парохода: один – на север, другой – на запад. С какой скоростью возрастает расстояние между ними, если скорость этих теплоходов 27 км/ч и 36 км/ч?
40. Тело массой 1 кг 100 г движется прямолинейно по закону x(t) = (6 – t)(2t + 3) – 18 (х выражена в метрах, t – в секундах). Найти импульс тела при t=1 с.
41. Температура тела изменяется по закону T(t) = 0,5t2 –– 2t
(Т выражена в кельвинах, t – в
секундах). Какова скорость изменения температуры
при 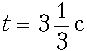 ?
?
42. Заряд q изменяется по закону q(t) = 0,5t2 + 0,4t (q выражен в кулонах, t – в секундах). Найти силу тока при t=4 с.
43. Лестница длиной 5 м вертикально прислонена к стене. В момент t=0 ее нижний конец начинает скользить по полу и равномерно отодвигается от стены со скоростью 2 м/с. Найти скорость, с которой верхний конец лестницы опускается в момент t=2 c.
44. Тело массой 500 г движется прямолинейно
по закону 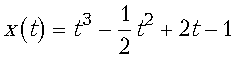 (х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=2 с.
(х
выражена в метрах, t – в секундах). Найти
силу, действующую на это тело в момент t=2 с.
45. Лестница длиной 4 м стоит вертикально,
прислоненная к стене. В момент t = 0 ее нижний
конец начинает скользить по полу и равномерно
отодвигается от стены со скоростью 1 м/с. Найти
скорость, с которой верхний конец лестницы
опускается в момент ![]() .
.
46. Тело массой 6 кг движется прямолинейно
по закону 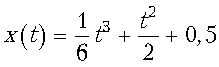 (х
выражена в метрах, t – в секундах). Найти
импульс тела при t=2 с.
(х
выражена в метрах, t – в секундах). Найти
импульс тела при t=2 с.
47. Определить ускорение колеблющегося тела в
момент t=3 с, если его координата
изменяется по закону 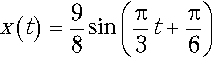 (х выражена в метрах, t –
в секундах).
(х выражена в метрах, t –
в секундах).
48. Заряд q изменяется по закону q(t) = t(0,3t + 2,6) (q выражен в кулонах, t – в секундах). Найти силу тока при t=3 с.
49. Определить скорость колеблющегося тела в
момент времени t=12 с, если его
координата изменяется по закону ![]() (х выражена в
метрах, t – в секундах).
(х выражена в
метрах, t – в секундах).
50. Маховик вращается по закону j(t) = t4 – 1 (j выражен в радианах, t – в секундах). Найти угловую скорость в момент времени t=2 с.
51. Угол поворота тела вокруг оси изменяется по закону j(t) = 0,5t2 (j выражен в радианах, t – в секундах). Найти угловую скорость при t=5 с.
52. Угол поворота тела вокруг оси изменяется по закону j(t) = 2,5t(t – 1) (j выражен в радианах, t – в секундах). Найти угловую скорость при t=8 с.
Итоговая таблица
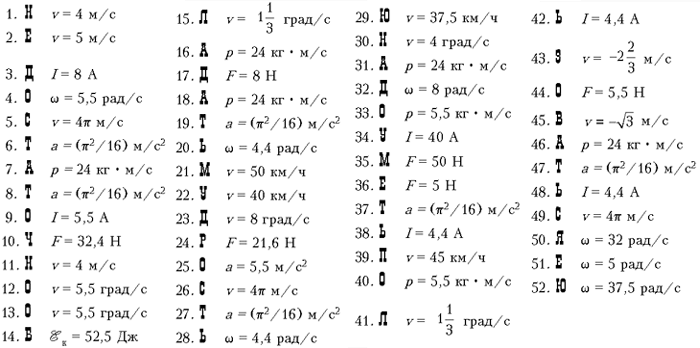
III. Решение задач
Учитель математики. Большую часть своих усилий человек тратит на поиск наилучшего, оптимального решения поставленной задачи: как добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальных затрат времени?
Не все задачи поддаются точному математическому описанию, не для всех найдены простые решения. Однако часть удается исследовать с помощью методов математического анализа, в частности те, которые можно свести к нахождению наибольшего или наименьшего значения функции. При решении будем пользоваться методом математического моделирования.
Задача 1 (№ 321, учебник: А.Н.Колмогоров и др. Алгебра и начала анализа. 10 кл. – М.: Просвещение, 2000).
Лодка находится на озере на расстоянии 3 км от ближайшей точки А берега. Пассажир желает достигнуть села В, находящегося на расстоянии 5 км от А (участок берега считаем прямолинейным). Лодка движется со скоростью 4 км/ч, а пассажир, выйдя из лодки, может в час по суше пройти 5 км. К какому пункту С берега должна пристать лодка, чтобы пассажир достиг села в кратчайшее время?
Анализ условия
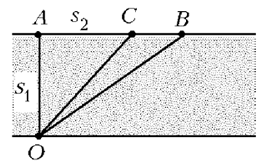
Сделаем рисунок. Что знаем о длине отрезков АВ? АО? Сравним скорости по воде и по суше. Как можно попасть в точку В? Одинаковым ли будет это время при разных положениях точки С? Почему?
Решение
 Применим
метод математического моделирования.
Применим
метод математического моделирования.
1. Составим функцию. Пусть АС = x. Тогда СВ = 5 – x. Выразим время t, которое понадобится, чтобы достичь пункта B, как функцию от x:
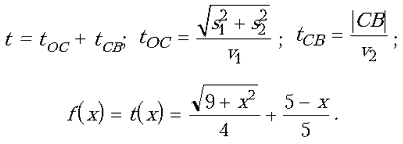
2. Исследуем f(x) на наименьшее значение на отрезке [0; 5]. Найдем производную от функции, приравняем ее к нулю, найдем корни уравнения f'(x) = 0, вычислим значение функции в этих точках. Выберем значение x, для которого функция минимальна (ученик делает это у доски):
.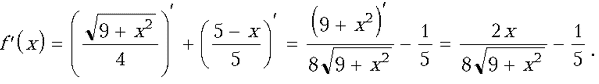
25x2 = 16 (9 + x2) Ю 9x2 = 144 Ю x2 = 16
Ю x1,2 = ±4.
3. Ответ. Чтобы затратить на путь из O в B наименьшее время, надо высадиться в 4 км от A.
Аналогичная задача на практике: выбор наиболее «быстрого» пути для доставки груза.
Учитель физики. На уроках физики нам довольно часто требуется установить зависимость одной физической величины от другой. Математические исследования могут помочь нам в этом.
Задача 2. Постройте график зависимости силы тока в полной цепи от внешнего сопротивления.
 Оборудование:
источник тока, прибор Ионтеля с двумя
проводниками равного сопротивления, амперметр,
вольтметр, соединительные провода.
Оборудование:
источник тока, прибор Ионтеля с двумя
проводниками равного сопротивления, амперметр,
вольтметр, соединительные провода.
Анализ условия. Как зависит сила тока в полной цепи от внешнего сопротивления? Вывести формулу закона Ома для такой цепи на доске.
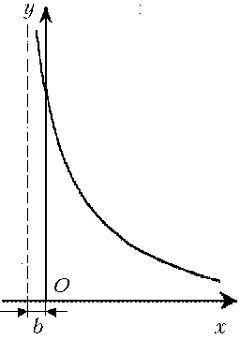
Учитель математики. Дома вы должны были
исследовать функцию 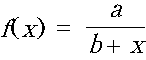 при a > 0, b > 0. На
доске ученик выписал результаты такого
исследования. График – это гипербола, смещенная
на b единиц влево; при x®b,
f(x)®Ґ. Пересечение с осью Oу –
в точке a/b.
при a > 0, b > 0. На
доске ученик выписал результаты такого
исследования. График – это гипербола, смещенная
на b единиц влево; при x®b,
f(x)®Ґ. Пересечение с осью Oу –
в точке a/b.
Учитель физики. Вид формулы закона Ома: 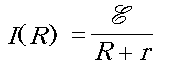
такой же, что и вид функции f(x), а значит, одинаков и вид графиков. Следовательно, ваше исследование можно использовать для выяснения зависимости силы тока от внешнего сопротивления. Аргументом будет R, физиков интересует только область значений аргумента R > 0. Почему?
Ученик. Причина сопротивления –
взаимодействие свободных электронов с узлами
кристаллической решетки. Его значение
определяется по формуле 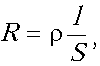 где l – длина
проводника, S – площадь
поперечного сечения, r –
удельное сопротивление – всегда положительные
величины.
где l – длина
проводника, S – площадь
поперечного сечения, r –
удельное сопротивление – всегда положительные
величины.
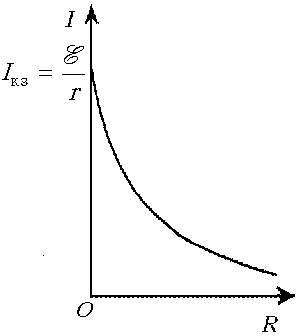 Учитель
физики. Следовательно, интересующий нас график
будет выглядеть следующим образом (убирает
лишнее в графике на доске, меняет обозначения
осей). Точка пересечения графика с осью ординат I
есть значение тока короткого замыкания
Учитель
физики. Следовательно, интересующий нас график
будет выглядеть следующим образом (убирает
лишнее в графике на доске, меняет обозначения
осей). Точка пересечения графика с осью ординат I
есть значение тока короткого замыкания 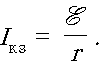 . Что называется
коротким замыканием?
. Что называется
коротким замыканием?
Ученик. Явление резкого возрастания тока при уменьшении внешнего сопротивления до нуля.
Учитель физики. Итак, мы выяснили, как выглядит теоретическая зависимость I(R). Получим эту зависимость эмпирически, т.е. опытным путем. Наметим план нашей экспериментальной работы:
1. Изменяя сопротивление, будем измерять силу тока.
2. Чтобы получить разные сопротивления из двух резисторов равного сопротивления, сначала соединим их параллельно (получим минимальное значение), затем возьмем только один (промежуточное значение), а потом соединим последовательно (максимальное).
3. Для определения Iкз измерим
вольтметром ![]() на
клеммах источника тока при разомкнутой цепи, а r
найдем по формуле
на
клеммах источника тока при разомкнутой цепи, а r
найдем по формуле 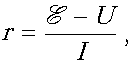 где U, I – соответственно
напряжение и сила тока в цепи при любом
резисторе.
где U, I – соответственно
напряжение и сила тока в цепи при любом
резисторе.
4. Данные занесем в таблицу (на доске и в тетради):
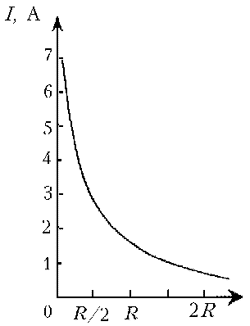 5. Вспоминаем
технику безопасности: приборы на столе следует
располагать рационально, все соединения
выполнять при отключенном источнике тока, в
случае неисправности цепь размыкать и ставить в
известность учителя, амперметр включать
последовательно, а вольтметр – параллельно
участку цепи.
5. Вспоминаем
технику безопасности: приборы на столе следует
располагать рационально, все соединения
выполнять при отключенном источнике тока, в
случае неисправности цепь размыкать и ставить в
известность учителя, амперметр включать
последовательно, а вольтметр – параллельно
участку цепи.
Ход работы. Учащиеся на местах – в группах по двое (а у доски – вызванные) – выполняют необходимые соединения, измерения, вычисления, заполняют таблицу, чертят график, делают вывод: вид экспериментальной зависимости совпадает с теоретической кривой, т.е. сила тока в полной цепи обратно пропорциональна сумме внешнего и внутреннего сопротивлений, и, главное, формула закона Ома для полной цепи справедлива.
Учитель указывает, кому по окончании урока сдать тетради.
IV. Закрепление новых знаний
Задача 3. Определите мощность P, отдаваемую электронагревательным элементом, имеющим сопротивление R и включенным в цепь источника тока с ЭДС 1 и внутренним сопротивлением r. Каким должно быть внешнее сопротивление R, чтобы отдаваемая элементом мощность была наибольшей?
Анализ условия и составление плана решения
Назначение нагревательного элемента – выделение тепла. Неизбежные потери – нагревание соединительных проводов, потери мощности на внутреннем сопротивлении источника. Мощность находим через работу тока во внешней цепи, т.е. через напряжение и силу тока, используя закон Ома для полной цепи.
Решение
Ученик записывает решение на доске, остальные – в тетрадях:
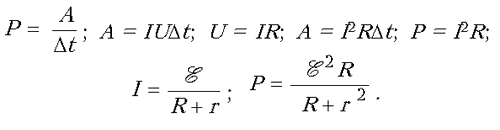
Учитель математики. Как мы сегодня учились находить максимальное значение величины? Ученики повторяют план исследования и находят значение R, при котором мощность наибольшая:
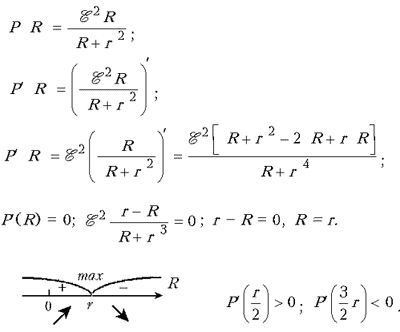
Ответ. Мощность P максимальна при сопротивлении внешнего резистора R=r.
V. Домашнее задание
- Батарея с ЭДС 12 В и внутренним сопротивлением 0,8 Ом питает поочередно внешние цепи, имеющие сопротивления 0,4; 0,8 и 2 Ом. В каком случае полезная мощность наибольшая? Определите КПД батареи. Когда он наибольший?
Учитель физики. Используйте решение классной задачи.
Ученики. Мощность выделяется наибольшая, когда
внутреннее сопротивление равно внешнему, т.е.
0,8 Ом.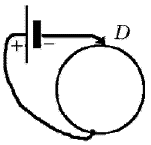
- Кольцо из однородной проволоки подключено к батарейке, имеющей нулевое внутреннее сопротивление. При каком положении движка D в кольце выделяется минимальное количество тепла?
Учитель физики. Какому закону подчиняется искомая физическая величина? Как соединены две части витка при произвольном положении движка? От чего зависит сопротивление каждой части? Как найти общее внешнее сопротивление? Функцией какой величины является количество выделившегося тепла? (Ученики отвечают, тем самым составляя план решения задачи.)
VI. Окончание урока
Учитель физики. Мы сегодня еще раз нашли точки соприкосновения двух наук – физики и математики. Говорят, что математика – служанка всех наук, в том числе и физики, – и пусть математики не обижаются. Зная математику, физики «вооружены», им по силам не только простые задачи. Галилей основал точное естествознание, Архимед в своих трудах по статике и гидродинамике дал образец применения математики в естествознании и технике, а великий Ньютон – математическое обоснование физических законов, для чего разработал дифференциальное и интегральное исчисления. И мы рады, что вы овладеваете таким математическим аппаратом, чтобы познавать мир и объяснять его. Вы это сможете. Сегодня вы начали учиться делать это. Спасибо всем, урок окончен.
Bместо послесловия
Совет методического объединения учителей физики г. Находки в составе Дмитриевой Л.А., Красюковой Т.С., Олейниковой Т.А., Войновой Л.В., Липковой Л.А., Карпушиной Н.А., Ермаковой Н.А. выражает благодарность учителям школы № 23 Ширяевой Татьяне Васильевне и Куликовой Любови Леонтьевне за бинарный урок, проведенный в 10-А классе на тему «Решение физических задач с помощью математического анализа».
Нестандартным было начало урока («Поле чудес»), в течение которого дети решили 52 задачи физического содержания на вычисление производной. Они совершенно самостоятельно выполняли задания, а учителя лишь корректировали их работу и подводили итоги.
На следующем этапе учитель математики использовала метод математического моделирования для исследования функции F(x) = a/x + b и вместе с учениками построила график этой функции. Затем учитель физики, записав закон Ома для полной цепи и используя те же приемы, исследовала теоретически зависимость I(R).
Следующим шагом была экспериментально-исследовательская работа учащихся. С помощью приборов, сняв необходимые показания, надо было подтвердить теоретические выводы. Для контроля несколько учащихся выполняли тот же эксперимент на демонстрационном столе. Построенный экспериментальный график зависимости I(R) убедительно доказал возможность использования приемов математического анализа для решения исследовательских задач физического характера.
На уроке были созданы условия для реализации креативных возможностей обучающихся. Татьяна Васильевна и Любовь Леонтьевна буквально «дирижировали» учебной деятельности. Высокий уровень подготовки позволил охватить большой объем учебного материала и полностью реализовать цели урока, продемонстрировать собранность, дисциплинированность, тактичность, демократичность преподавателей. Образцом была четкая, грамотная речь учителей, красота записей на доске, красота эксперимента.
Присутствовавшие на уроке учителя получили положительный эмоциональный заряд от общения с коллегами и оценили его на «отлично»: Татьяна Васильевна и Любовь Леонтьевна убедительно подтвердили в очередной раз, что они являются учителями высшей категории.
