Что значит измерить физическую величину правильно? На этот вопрос ответить непросто. Обычно ученики смешивают два понятия: правильно и точно. «Часто стараются произвести измерения с наибольшей достижимой точностью, т.е. сделать ошибку измерений по возможности малой. Однако следует иметь в виду, что чем точнее мы хотим измерить, тем труднее это сделать. Поэтому не следует требовать от измерений большей точности, чем это необходимо для решения поставленной задачи. Для изготовления книжной полки длину досок вполне достаточно измерять с точностью 0,5–1 см, или около 1%; для изготовления некоторых деталей шарикоподшипников нужна точность 0,001 мм, или около 0,01%, а при измерении длин волн спектральных линий необходима иногда точность 10–11 см, или около 10–5%» [1]. Измерить правильно – это прежде всего определить точность, необходимую для решения конкретной задачи. Затем следует выбрать метод измерений и приборы. И наконец, правильно измерить – значит правильно указать интервал значений, в котором лежит измеренная величина. Однако для учеников подобные рассуждения не являются наглядными до тех пор, пока они не подкреплены практической задачей.
Предлагаемый материал можно рассматривать как подготовку к нескольким факультативным занятиям на тему «Что значит измерить физическую величину правильно?». В той или иной форме он был апробирован на уроках физики в 9-х физико-математических и химико-биологических классах нашей гимназии.
Любая практическая работа по измерению начинается с теоретической оценки интервала значений, в котором может лежать измеряемая величина. Выполнить эту работу ученик может и дома, если ему будут предоставлены соответствующие исходные данные и расчетные формулы.
Расчет средней плотности яйца. Прежде всего нужно выяснить, что представляет собой куриное яйцо. Кратко строение и физико-химические свойства объекта измерений можно раздать учащимся в распечатках типа приведеной ниже (сведений в ней приведено значительно больше, чем требуется для определения плотности, – ученик должен уметь выбрать необходимое).
Физико-химические свойства куриного яйца [2–4]
Масса 45–65 г, в среднем яйце содержится (по
массе) 32% желтка, 56% белка, 12% скорлупы,
энергетическая ценность 314 Дж.
Желток представляет собой густую, желтоватую
массу из множества форменных тел – желточных
шаров, и состоит из особого белка, именуемого
вителлином (относящегося к глобулинам), лицетина
– вещества, содержащего фосфор, холестеарина,
или желточного масла – желтого красящего
вещества лутеина, – и минеральных солей, среди
которых преобладают фосфаты калия; в желтке
также имеется и железо.
Белок отличается от желтка отсутствием
желточных шаров. Он представляет собой
конгломерат крайне тонкостенных клеток,
содержимое которых состоит преимущественно из
богатого водой белка. кроме того, в белке имеется
некоторое количество омыленных жиров, сахар,
принимаемый за виноградный, и соли, среди которых
преобладает поваренная. Белок куриного яйца
содержит по массе 10–13% белка (глобулины,
альбумины, альбумозы), 85% воды, 0,7% поваренной соли,
остальное в основном жиры.
Замечательно, что распределение солей между
желтком и яичным белком аналогично
распределению их в крови
между кровяными шариками и плазмой: в желтке, как
и в кровяных шариках, преобладают фосфаты калия,
тогда как в яичном белке преобладает хлорид
натрия.
Средний химический состав яйца (без скорлупы) по массе:
Яйцо не обладает большой устойчивостью к хранению. Через поры скорлупы испаряется вода, и на тупом конце образуется пуга – пространство, заполненное воздухом. Свежесть яйца можно проверить опусканием в холодную воду: лежалые яйца тонут медленнее, чем свежие.
Приблизительная плотность некоторых веществ, входящих в состав яйца:
Плотность расчитывают, используя свойство аддитивности удельных объемов веществ, не реагирующих химически:
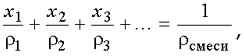
где х – массовая доля компонента (если, например, содержание по массе 30%, то массовая доля 0,3), r – его плотность. Кратко опишем расчеты, проводимые учеником дома.
= (0,648 + 0,083 + 0,114 + 0,003 + 0,004 + 0,044) см3/г = 0,896 см3/г.
Следовательно, rяйца » 1,1 г/см3.
Ответ. Средняя плотность яйца без учета наличия воздушного пузырька (пуги) составляет около 1,1 г/см
3.Как видим, плотность яйца чуть превышает 1 г/см3, т.е. яйцо чуть тяжелее воды. Таким образом, можно предложить два метода определения плотности яйца: «грубый» – метод Архимеда, и более точный – метод безразличного плавания.
Метод Архимеда. Опустив яйцо в воду, по объему вытесненной воды определяем объем яйца, взвешиваем яйцо на весах, находим массу и вычисляем плотность.
Оборудование: отливной сосуд, мензурка (100 мл), весы с разновесами, яйцо.
Расчет ошибки
Косвенная ошибка измерения плотности [5, с. 366–368]:
где Dm = Dвесов + Dвсех гирь + Dподбора гирь – абсолютная ошибка измерения массы, Dвесов – инструментальная погрешность, Dвсех гирь – суммарная погрешность массы использованных разновесов (см. таблицу ниже), Dподбора гирь – погрешность подбора гирь, равная половине массы наименьшей гири; DV – абсолютная ошибка измерения объема.
Пример. Пусть найденная экспериментально масса яйца составляет m = 56,96 г = 50 г + 5 г + 1 г + 500 мг + 200 мг + 200 мг + 50 мг + + 10 мг, его объем V = 152 мл = 152 см3.
Взвешивание проводилось на арретированных технических весах чувствительностью 5 мг. Однако с увеличением массы взвешиваемого тела погрешность возрастает, и при m»57 г, согласно паспорту, Dвесов»100 мг.
По таблице:
определяем погрешность всех гирь: Dmвсех гирь = (30 + 8 + 4 + 3 + 2 + 2 + 1 + 1) мг = 51 мг.
Погрешность подбора гирь Dподбора гирь = 5 мг.
В итоге абсолютная ошибка Dm = (100 + 56) мг » 160 мг, а относительная ошибка Dm/m » 0,3%.
Абсолютная ошибка измерения объема DV»1 мл = 1 cм3, а относительная ошибка составляет DV/V»1,5%. Эта ошибка и определяет в значительной степени погрешность определяемой плотности.
Неучтенной осталась еще методическая ошибка, которая будет обсуждена ниже.
Ход работы
1. Уравновесьте чашки весов; запишите инструментальную погрешность весов.
2. Взвесьте исследуемое тело, запишите массу тела. Выходит ли масса данного куриного яйца за общепринятые пределы?
3. Выпишите номинальные массы гирь разновесов и соответствующую им ошибку измерений согласно таблице. Вычислите ошибку измерения массы:
Dm = Dвесов + Dвсех гирь + Dподбора гирь.
4.
Наполните отливной сосуд водой; подставьте
химический стакан (100 мл) под отлив, медленно
опустите яйцо в воду.
5. Убедившись, что вся вытесненная вода перетекла в стакан, вылейте эту воду в мензурку объемом 100 мл. Определите объем вытесненной жидкости и запишите этот объем с учетом ошибки.
6. Вычислите плотность тела по формуле: 
7. Запишите полученный результат с учетом ошибки измерений.
8. Эскизно изобразите проведение опыта (рис. 1).
Метод безразличного плавания: «…если вес тела в точности равен весу вытесненной жидкости, оно будет находиться в равновесии внутри жидкости. Например, куриное яйцо тонет в пресной воде, но плавает в соленой. Можно сделать раствор соли, концентрация которого постепенно уменьшается кверху, так что выталкивающая сила внизу сосуда больше, а вверху – меньше веса яйца. В таком растворе яйцо держится на такой глубине, где его вес равен выталкивающей силе. Если твердое тело однородно, т.е. во всех точках имеет одну и ту же плотность, то тело будет тонуть, всплывать или оставаться в равновесии внутри жидкости в зависимости от того, больше ли плотность тела плотности жидкости, меньше или равна ей. В случае неоднородных тел нужно сравнивать с плотностью жидкости среднюю плотность тела» [6]. Значит, можно подобрать такой однородный раствор соли в воде, в котором яйцо плавает на некоторой глубине. Плотность раствора можно измерить с помощью ареометра. поскольку само измерение плотности занимает немного времени, четырех-пяти ареометров на класс достаточно
Этот
метод применяется в лабораторной практике при
определении, например, плотности мелких
кристаллов в достаточно широких пределах. Для
этого смешением нескольких жидкостей разной
плотности подбирается такой раствор, в котором
кристаллик плавает в толще жидкости. Из
приведенной таблицы видно, что, например,
алюминий должен плавать в дииодметане. Следует
заметить, что не все приведенные в таблице
жидкости между собой смешиваются и не все
безопасны в обращении.
Оборудование: мензурка (250 мл), мерный стакан (400 мл), химический стакан (250 мл), ареометр, насыщенный раствор поваренной соли, стеклянная палочка.
Ошибка измерений в данном случае определяется ценой деления ареометра (например 0,002 г/см3) и, следовательно, составляет половину цены деления (т.е. около 0,1%), т.е. сравнима с ошибкой определения массы в первом методе.
Ход работы
1. Убедитесь, что ареометр предназначен для измерения плотностей, которые больше 1 г/см3. Определите цену деления ареометра.
2. Положите яйцо на дно мерного стакана (400 мл), налейте чистой воды до половины.
3. Начните доливать крепкий раствор поваренной соли, слегка помешивая стеклянной палочкой, до тех пор, пока яйцо не начнет отрываться от дна. Убедитесь, что яйцо не всплывает на поверхность. Если яйцо всплыло, долейте чистой воды, чтобы уменьшить плотность раствора.
4. Перелейте раствор в мензурку. Аккуратно опуская ареометр в мензурку, измерьте плотность раствора. Запишите полученное значение с учетом ошибки измерений.
5. Эскизно изобразите проведение опыта (рис. 2), укажите силы, действующие на яйцо, плавающее в мерном стакане.
Рис. 2. Определение плотности тела по методу безразличного плавания
Контрольные вопросы (их можно задать при устном обсуждении результатов работы, а можно включить в текст обязательных заданий)
Анализ полученных результатов
Проведение измерений занимает в среднем чуть больше урока. Важно проанализировать полученные результаты вместе с учащимися. Первым методом получается плотность (0,9–1,1) г/см3, вторым методом – в среднем – (1,05 –1,07) г/см3. Следует обратить внимание на то, что разброс результатов больше ошибки ареометра. Это связано с тем, что важным элементом любой экспериментальной работы является навык. Разброс данных в первую очередь связан с тем, что, во-первых, соответствующую плотность раствора подобрать сложно, а во-вторых, яйца не выпускаются по стандарту – они продукт живой природы. Результаты нужно изобразить на доске в виде отрезков.
Плотности, полученные по методу Архимеда, заключены на отрезке [0,9; 1,1], куда входят и плотности, полученные более точным методом, – отрезок [1,05; 1,07].
Как и ожидалось, более точные значения оказались чуть ниже теоретической оценки, т.к. при расчете мы не учли объем воздушного пузырька. (Нужно объяснить ученикам, что всегда существует неучтенный фактор, не всегда удается найти источник ошибок.)
Далее можно обсудить, каковы источники ошибок в методе Архимеда:
Следующий вопрос: «А как улучшить метод?» Прогнозируемый ответ ребят: определить объем вытесненной воды путем взвешивания. Не следует отвергать это в общем-то здравое предложение. Однако для его реализации нужно проделать как минимум еще две измерительные операции: взвесить пустой, а затем полный сосуд с вылившейся водой, а также учесть ошибку каждого измерения. Последнее отнимает гораздо больше времени, чем само измерение. Громоздкость измерения увеличивается, а точность… Взвешивание вылившейся воды не компенсирует двух других недостатков метода, которые вносят почти такую же ошибку измерения (до 0,5 мл). Следовательно, еще раз можно вернуться к мысли, высказанной в начале статьи: точность приборов для проведения измерений нужно выбирать в согласии с поставленной задачей и выбранным методом. Не нужно оставлять у ребят иллюзий, что второй метод безупречен: плотность жидкости зависит от температуры, стеклянный ареометр чуть больше погружается в воду из-за образования мениска, поскольку стекло смачивается водой. Однако это погрешности совсем другого порядка малости по сравнению с погрешностями первого метода.
Таким анализом ошибок и заканчивается занятие.
1. Зайдель А.Н. Ошибки измерений физических величин. – Л.: Наука, 1974.
2. Краткая энциклопедия домашнего хозяйства. Т. 2. – М.: Большая Советская Энциклопедия, 1959.
3. БСЭ/ Изд. 1-е. – М.: Советская Энциклопедия, 1926–1947.
4. Химическая энциклопедия. – М.: Советская Энциклопедия, 1988–1998.
5. Физика-10./Под ред. А.А.Пинского. – М.: Просвещение, 1993.
6. Ландсберг Г.С. Элементарный учебник физики. Т. 1. – М.: АОЗТ «Шрайк», 1995.
.
