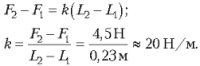
Расчетные задачи
1. (I) Резиновая лента имеет длину L1=145 см,
если к ней приложена сила F1=18,0 H,
и длину L2=168 см, если сила равна F2=22,5 H.
Найдите жесткость ленты.
A piece of rubber is 145 cm long when a weight of 18.0 N hangs from it and is 168 cm long when a weight of 22.5 N hangs from it. What is the «spring» constant of this piece of rubber?
Решение
F1 = k(L1 – L0);
F2 = k(L2 – L0),
где L0 – длина нерастянутой ленты.
Тогда
2. (I) Когда человек массой m=80 кг садится в машину массой M=1000 кг, ее рессоры сжимаются по вертикали на Dx = 1,40 см. Найдите частоту вертикальных колебаний машины при езде по буграм.
When an 80-kg person climbs into a 1000-kg car, the car,s springs compress vertically by 1.40 cm. What will be the frequency of vibration when the car hits a bump? (Ignore damping.)
Решение
3. (I) Пружину оттянули на А = 20 см и отпустили.
а) Напишите закон движения пружины, если
известно, что период ее колебаний равен Т=0,75 с.
б) Каково смещение пружины через t = 1,8 с после
начала колебаний?
(a) What is the equation describing the motion of a spring that is stretched 20 cm from
equilibrium and then released, and whose period is 0.75 s?
(b) What will be its displacement after 1.8 s?
Решение
При t = 1,8 с смещение 
4. (I) Таракан массой m1=0,30 г попал в паутину,
которая начала дрожать с частотой n1=10
Гц.
а) Чему равна эффективная жесткость k паутины?
б) С какой частотой будет дрожать эта паутина,
если в нее попадется насекомое массой m2=0,10
г?
A small cockroach of mass 0.30 g is caught in a spider,s web. The web vibrates predominately with a frequency of 10 Hz. (a) What is the value of the effective spring constant k for the web? (b) At what frequency would you expect the web to vibrate if an insect of mass 0.10 g were trapped?
Решение
Отсюда: 
5. (II) На конце пружины подвешен груз. Его оттягивают на 8,0 см от положения равновесия и отпускают. а) На каком расстоянии от положения равновесия его скорость будет равна половине максимальной? б) На каком расстоянии от положения равновесия его ускорение будет равно половине максимального?
A mass on the end of a spring is stretched 8.0 cm from equilibrium and released. At what distance from equilibrium will it have (a) velocity equal to half its maximum velocity and (b) acceleration equal to half its maximum acceleration?
Решение
Запишем выражения для смещения, скорости и ускорения груза в произвольный момент времени t:
а) Максимальная скорость составляет Aw,
скорость равна половине максимальной при 
при этом 
тем самым искомое
расстояние до положения равновесия составляет 
б) Ускорение связано со смещением соотношением 
т.е. если
ускорение равно половине максимального, то и
смещение равно половине максимального. Поэтому
искомое расстояние равно x = A/2 = 4 см.
.
