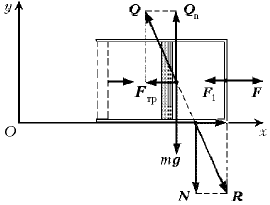
Задача 70. В цилиндрический стакан, лежащий на боку на горизонтальной плоскости, начинают медленно вдвигать гладкий поршень. Найдите давление воздуха в цилиндре в тот момент, когда цилиндр сдвинется с места. Масса стакана вместе с поршнем m=2 кг, площадь поршня S=6 см2, атмосферное давление p0 = 100 кПа, коэффициент трения между плоскостью и цилиндром m=0,3.
Дано: СИ m = 2 кг, S = 6 см2, 6 • 10–4 м2, p0 = 100 кПа, 105 Па. m = 0,3.
p – ?
Анализ условия
Цилиндр вместе с поршнем взаимодействует с Землей, плоскостью и воздухом. Поэтому на них действуют сила тяжести mg, реакция опоры Q, а также силы давления со стороны воздуха. Цилиндр с поршнем действует на плоскость с силой R. На поршень также действует сила, с которой его вдвигают в цилиндр, направленная горизонтально.
Реакция опоры Q направлена под углом к вертикали, т.к. между цилиндром и плоскостью существует трение. Сила трения меняется от нуля, когда поршень только начинают вдвигать в цилиндр, до своей максимальной величины, называемой максимальной силой трения покоя fmax, равной силе трения скольжения.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной. Запишем уравнение движения цилиндра для того момента, когда он начинает двигаться:
mg + Q + F + F1 = 0,
где F – сила давления воздуха в стакане на его дно, F1 – сила давления атмосферного воздуха.
Спроектируем это векторное равенство на оси координат:
Ox: –fmax + F – F1 = 0;
Oy: –mg + Qn = 0.(1)
(2)
По закону Кулона, fmax = mN, где N – сила нормального давления – составляющая силы R на направление, перпендикулярное плоскости.
По третьему закону Ньютона, Q = –R, тогда для проекций на ось Oy получаем Qn = –(–N) = N.
Следовательно, с учетом уравнения (2): fmax = mN = mQn = mmg.
Тогда из уравнения (1) получаем F = fmax + F1.
По определению, F = pS; F1 = p0S. Тогда
Проверка решения по размерности
С этой точки зрения задача решена верно, тогда
Комментарий редактора
Приводим более короткое и ясное решение.
Анализ условия
Для начала сделаем более четкий рисунок.
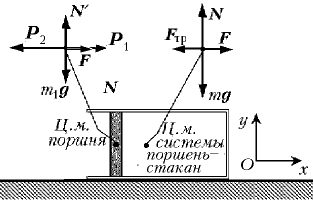
По условию задачи, поршень в цилиндрический стакан вдвигают медленно, поэтому будем считать, что центр масс (ц.м.) системы поршень–стакан движется до начала скольжения стакана с ускорением, близким к нулю.
На систему поршень–стакан действуют следующие внешние силы: сила тяжести mg (m – суммарная масса поршня и стакана), внешняя сила со стороны человека, вдвигающего поршень, F и сила реакции опоры, состоящая из нормальной составляющей N и силы трения Fтр. Равнодействующая сил, действующих на систему со стороны воздуха снаружи стакана, равна нулю.
Рассмотрим теперь поршень. На поршень действуют следующие силы: сила тяжести m1g (m1 – масса поршня), сила реакции опоры N ', направленная вертикально вверх, т.к. сила трения между поршнем и стаканом, по условию задачи, отсутствует, сила давления Р1 = i(p0S), действующая со стороны воздуха, находящегося снаружи стакана, и сила Р2 = –i(pS), действующая со стороны воздуха, находящегося в стакане (i – единичный вектор в направлении оси x). Ускорение поршня, учитывая условие «медленности», будем считать равным нулю.
Решение
Запишем 2-й закон Ньютона для системы поршень–стакан до начала скольжения стакана:
Ox: 0 = – Fтр + F;
Oу: 0 = N – mg.(1)
(2)
То же для поршня:
Ox: 0 = F + p0S – pS; (3)
Ox: 0 = N ' – m1g.
Из (1) и (3) получаем
Давление будет нарастать до тех пор, пока Fтр не достигнет своей максимальной величины f max, приближенно равной силе трения скольжения, т.е. с учетом (2): fmax = mN = mmg.
Итак, давление в момент проскальзывания:
Задача 71. Два одинаковых шарика массой m = 0,09 кг каждый заряжены одинаковыми электрическими зарядами и подвешены при помощи непроводящих невесомых нитей к потолку один под другим. Какой заряд должен иметь каждый шарик, чтобы обе нити испытывали одинаковое натяжение? Электростатическим взаимодействием шариков с потолком пренебречь. Расстояние между шариками l = 0,3 м, электрическая постоянная e0 = 8,85 • 10–12 Ф/м , ускорение свободного падения g = 10 м/с2.
Дано:
m = 0,09 кг,
l = 0,3 м,
e0 = 8,85 • 10–12 Ф/м ,
g = 10 м/с2,
T1 = T2.
__________
q – ?
Анализ условия
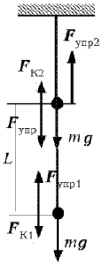Нижний шарик взаимодействует с
Землей, нижней нитью и с другим шариком, поэтому
на него действуют сила тяжести mg, сила упругости Fупр1
нити и кулоновская сила FК1.
Нижняя нить взаимодействует с шариками, которые на нее действуют силами натяжения: нижний – с силой –T1, верхний – с силой –T.
Верхний шарик взаимодействует с Землей, другим шариком, а также с верхней и нижней нитями. Следовательно, на него действуют: сила тяжести mg, кулоновская сила FК2 и силы упругости нитей Fупр – со стороны нижней и Fупр2 – со стороны верхней.
На верхнюю нить со стороны верхнего шарика действует сила натяжения T2.
Под действием этих сил каждое тело из рассматриваемой системы находится в равновесии.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной. Запишем условия равновесия для каждого из тел системы шарики-нити:
для нижнего шарика: mg + FК1 + Fупр1 = 0;
для нижней нити: T1 + T = 0;
для верхнего шарика: mg + FК2 + Fупр + Fупр2 = 0.
Спроектируем записанные векторные равенства на ось Oy:
mg + FК1 – Fупр1 = 0,
T1 – T = 0,
mg – FК2 + Fупр – Fупр2 = 0.(1)
(2)
(3)
По третьему закону Ньютона:
Fупр1 = T1; Fупр2 = T2; Fупр = T1.
Тогда с учетом условия задачи Т1 = Т2 и уравнения (2):
Fупр1 = T1 = T2 = Fупр2 = T = Fупр.
Уравнения (1) и (3) примут вид:
Отсюда: T = 2mg и FК1 = T – mg = 2mg – mg = mg.
По закону Кулона,
Таким образом, заряды шариков могут быть как положительными, так и отрицательными, но обязательно одного знака.
Проверка решения по размерности
С этой точки зрения задача решена верно, тогда:
Комментарий редактора
Приводим более простое решение.
Анализ условия
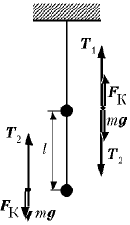По условию задачи, нити невесомые,
поэтому силы натяжения верхней нити T1 и
нижней нити T2 на всем протяжении постоянны.
Центр масс верхнего шарика будет двигаться под
действием сил: притяжения к Земле mg, сил
упругости нитей T1 и T2 и кулоновской
силы Fк. Центр масс нижнего шарика будет
двигаться под действием силы взаимодействия с
Землей mg, силы упругости нижней нити T2 и
кулоновской силы Fк.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной. запишем условия равновесия для каждого из тел системы шарики–нити:
для верхнего шарика: mg + T2 = Fк + T1; (1)
для нижнего шарика: mg + Fк = T2.
По условию задачи, T1 = T2. Тогда из (1) mg = Fк.
По закону Кулона,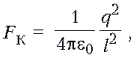 
следовательно, 
Л.Е. Свистов, канд. физ.-мат. наук
