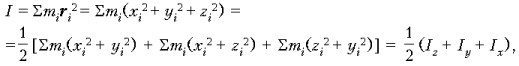Контроль знаний
Задачи из-за кордона
(продолжение. См. № 1, 5, 9, 13, 17, 21, 25, 29/01)
Кинематика и динамика вращательного движения
38. (I) Найдите момент инерции велосипедного колеса диаметром 68 см и суммарной массой обода и шины 1,3 кг. Объясните, почему массой ступицы при расчете можно пренебречь.
Calculate the moment of inertia of a 68-cm-diameter bicycle wheel. The rim and tire together have a mass of 1.3 kg. Why can the mass of the hub be ignored?
Решение
Момент инерции обруча равен I = mR2. Подставляя m = 1,3 кг, R = 0,34 м, находим I = 1,3 • (0,34)2 = 0,15 (кг • м2).
39. (I) Молекула кислорода состоит из двух атомов кислорода суммарной массой 5,3 Ч 10–26 кг. Момент инерции молекулы относительно оси, проходящей через ее центр масс перпендикулярно соединяющему атомы отрезку, равен 1,9 Ч 10–46 кг Ч м2. Оцените эффективное расстояние между атомами.
An oxygen molecule consists of two oxygen atoms whose total mass is 5.3 • 10–16 kg and whose moment of inertia about an axis at its center and perpendicular to the line joining them is 1.9 • 10–46 kg•m2. Estimate, from these data, the effective distance between the two atoms.
Решение
Момент инерции молекулы О2
равен моменту инерции гантели I = 2mR2, где m –
масса атома, M = 2m – суммарная масса. Отсюда
расстояние между атомами 
Подставляя заданные значения,
получаем d=1,2•10–10м.
40. (I) Используя теорему
Штейнера, найдите момент инерции тонкого
однородного стержня массой m и длиной L
относительно оси, перпендикулярной стержню и
проходящей через его конец. Известно, что момент
инерции стержня относительно его центра масс
равен 
Use the parallel-axis theorem to show that the moment
of inertia of a thin rod about an axis perpendicular to the rod at one end is 
assuming that if the axis passes
through the center, 
.
Решение
Теорема Штейнера утверждает, что если I0 – момент инерции тела (системы тел) относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии a от нее, равен I = I0 + ma2, где m – полная масса тела.
Разобьем мысленно тело на
отдельные материальные точки с массами mi и
радиус-векторами ri (относительно центра масс). По
определению, момент инерции 
При параллельном смещении оси, относительно
которой рассчитывается момент инерции, на вектор
a, новый момент инерции запишется как 
Мы использовали определение центра масс,
согласно которому в системе центра масс 
и возможность
выносить общий множитель (в том числе вектор) за
знак суммы.
41. (II) Используя связь между моментами инерции относительно точки и относительно трех взаимно перпендикулярных осей, проходящих через эту точку, найдите момент инерции тонкой плоской квадратной пластины со стороной s относительно оси, проходящей через центр пластины: а) вдоль ее диагонали; б) параллельно одной из сторон.
Use the perpendicular-axis theorem to determine a formula for the moment of inertia of a thin, square plate of side s about an axis (a) through its center and along a diagonal of the plate, (b) through the center and parallel to a side.
Решение
Три перпендикулярные оси образуют прямоугольную декартовую систему координат. Обозначим оси соответственно x, y, z. Тогда момент инерции относительно точки начала координат можно записать в виде (см. решение задачи 40):
где Ik – момент инерции относительно k-й оси.
Для плоских тел момент инерции относительно точки (например центра масс) совпадает с моментом инерции относительно оси, проходящей через эту точку перпендикулярно плоскости тела. Этот момент называется полярным моментом инерции. Момент относительно оси, лежащей в плоскости тела, называется экваториальным. Из доказанного выше следует, что полярный момент плоского тела равен сумме двух экваториальных, оси которых взаимно перпендикулярны. Из симметрии квадрата следует, что экваториальные моменты для осей, направленных по диагонали и вдоль одной из сторон, одинаковы.
Для квадратной пластины проще
всего находится момент инерции относительно
экваториальной оси, проходящей через центр
параллельно одной из сторон: он такой же, как для
однородного стержня длины s (относительно его
центра масс). Согласно условию задачи 40 он равен 
Используя симметрию квадрата, отсюда легко найти
полярный момент инерции 
42. (II) Найдите момент инерции тонкого обруча радиусом R и массой m относительно оси, направленной по касательной к обручу.
Determine a formula for the moment of inertia of a thin hoop of radius R and mass M about an axis tangent to its circular outline.
Решение
Используя решения задач 40 и 41,
находим 
43. (II) Два одинаковых однородных шара массой m и радиусом r0 каждый соединены тонким невесомым стержнем длиной r0, так что центры шаров находятся на расстоянии 3r0 друг от друга. Определите момент инерции системы относительно оси, перпендикулярной стержню и проходящей через его центр. Какой будет ошибка, если считать массу каждого шара сосредоточенной в его центре?
Two uniform solid spheres of mass M and radius r0 are connected by a thin (massless) rod of length r0 so that the centers are 3r0 apart. (a) Determine the moment of inertia of this system about an axis perpendicular to the rod at its center. (b) What would be the percentage error if the masses of each sphere were assumed to be concentrated at their centers and a very simple calculation were made?
Решение
Момент инерции шара
относительно оси, проходящей через его центр,
равен 
Действительно, момент инерции Ic
относительно центра шара равен 
если учесть, что dm = r4pr2dr, 
Согласно решению задачи 41: 
Используя теорему Штейнера и свойство аддитивности момента инерции, находим искомую величину I = 5,3mr02. Этот результат точный.
Если считать массу каждого шара сосредоточенной в его центре, то искомый момент равен I1 = 4,5mr02. Отклонение от точного ответа составляет 18%.
44. (II) Два однородных диска одинаковой толщины радиусами R1 и R2 соответственно касаются плоскими основаниями так, что их центры совпадают. Найдите момент инерции системы относительно оси, проходящей через центры дисков перпендикулярно их основанию. Плотности дисков одинаковы, суммарная масса дисков m.
The flat sides of two uniform solid cylindrical wheels of radii R1 and R2 are placed next to each other with their centers superposed. They are of equal thickness and are made of material of equal density. Find the moment of inertia of the system in terms of R1, R2, and M, the total mass of the system, as calculated about an axis passing through their centers perpendicular to the faces of the wheels.
Решение
Момент инерции тела
цилиндрической формы относительно оси симметрии
равен 
(см.
решение задачи 25). Из условия следует, что 
Сумма масс равна m, отсюда 
Момент инерции системы равен 
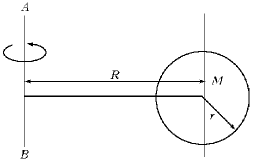45. (II) Шар массой m и радиусом r,
закрепленный на конце тонкого невесомого
стержня, вращается в горизонтальной плоскости
вокруг оси АВ по окружности радиусом R.
Расчитайте момент инерции системы относительно
оси АВ точно и приближенно, считая, что вся масса
шара сосредоточена в его центре. Найдите ошибку,
возникающую во втором случае, для r = 10 см и R = 1 м.
A ball of mass M and radius r on the end of a thin massless rod is rotated in a horizontal circle of radius R about an axis of rotation AB, as shown in Figure. (a) Considering the mass of the ball to be concentrated at its center of mass, calculate its moment of inertia about AB. (b) Using the parallel-axis theorem and considering the finite radius of the ball, calculate the moment of inertia of the ball about AB. (c) Calculate the percentage error introduced by the point mass approximation for r = 10 cm and R = 1.0 m.
Решение
Задачи решены Ю.А.Кокшаровым и А.В.Берковым