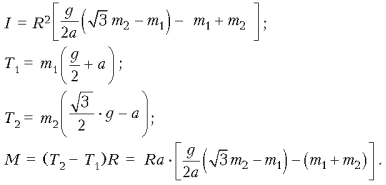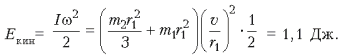Контроль знаний
Задачи из-за кордона
Кинематика и динамика вращательного движения
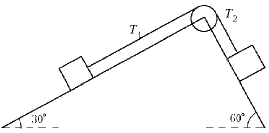32. (II) Два тела массами m1 = 8 кг
и m2 = 10 кг соединены легкой нерастяжимой
нитью, перекинутой через блок радиусом 25 см,
обладающий моментом инерции I. Тела имеют
ускорение a = 1 м/с2. Определите силы
натяжения T1 и T2 участков нити,
указанных на рисунке, момент сил, действующих на
блок, и величину его момента инерции.
Two blocks are connected by a light string passing over a pulley of radius 0.25 m and moment of inertia I. The blocks move to the right with an acceleration of 1.0 m/s2 on inclines with frictionless surfaces (see Figure). (a) Draw a force diagram for the two blocks and the pulley. (b) Determine T1 and T2, the tensions in the two parts of the string. (c) Find the net torque acting on the pulley, and determine its moment of inertia, I.
Решение
Обозначим угловую скорость блока через w, его ускорение через a. Из нерастяжимости нити следует, что wR = v, где R – радиус блока, v – линейная скорость тел. Для ускорений выполняется аналогичное соотношение: aR=a. Запишем уравнения движения тел и блока:
T1 – m1g sin30° = m1a;
m2g sin60° – T2 = m2a;
(T2 – T1)R = Ia.
Решая эту систему уравнений, получаем:
33. (II) При броске мяча массой 9 кг с
ускорением 8 м/с2 работают мышцы предплечья
– трицепсы. Оцените необходимый для такого
броска момент силы и величину самой силы,
используя данные, обозначенные на рисунке.
Массой руки пренебречь.
The forearm in Figure accelerates a 9.0-kg ball at 8.0 m/s2 by means of the triceps muscle as shown. Calculate (a) the torque needed and (b) the force that must be exerted by the triceps muscle. Ignore the mass of the arm.
Решение
Будем считать, что при броске рука вращается в локтевом суставе, причем плечо силы, создаваемой трицепсом, равно r1 = 2,5 см, а кисть движется по окружности радиусом r2 = 30 см. Тогда уравнение вращательного движения запишется в таком виде: M = Fr1 = mr22a = mr2a = 21,6 НЧм. Отсюда получаем F = 864 Н.
34. (II) Два груза массами m1 = 3,8 кг и m2 = 3,4 кг соединены невесомой нерастяжимой нитью, перекинутой через блок. Блок представляет собой однородный цилиндр радиусом R = 3 см и массой m3 = 0,8 кг. Найдите: а) ускорения грузов, считая, что трением можно полностью пренебречь; б) средний момент силы трения в оси блока, если известно, что при начальном движении груза m1 вниз со скоростью 20 см/с он останавливается через 6,2 с.
A string passing over a pulley has a 3.8-kg mass hanging from one end and a 3.40-kg mass hanging from the other end. The pulley is a uniform solid cylinder of radius 3.0 cm and mass 0.80 kg. (a) If the bearings of the pulley were frictionless, what would be the acceleration of the two masses? (b) In fact, it is found that if the heavier mass is given a downward speed of 0.20 m/s, it comes to rest in 6.2 s. What is the average frictional torque acting on the pulley?
Решение
Момент инерции блока I = 0,5 m3 R2 = 3,6Ч10–4 кгЧ м2.
Воспользуемся уравнениями, полученными при решении задачи 33, положив в них все углы равными 90°:
m1g – T1 = m1a;
T2 – m2g = m2a;
(T1 – T2)R – Mтр = Ia/R.
Если момент силы трения Mтр равен нулю, то для ускорений грузов имеем
Если известно ускорение грузов, то можно найти момент силы трения
В нашем случае a = –v0/t. Отсюда Мтр = 0,13 НЧм.
35. (III) Тонкий однородный стержень длиной L, стоявший вертикально на столе, начинает падать так, что его нижний конец не проскальзывает. Определите угловую скорость стержня как функцию угла j его наклона к плоскости стола. Чему равна скорость верхнего конца стержня непосредственно перед ударом о стол?
A thin rod of length L stands vertically on a table. The rod begins to fall, but its lower end does not slide. (a) Determine the angular velocity of the rod as a function of the angle j it makes with the tabletop. (b) What is the speed of the tip of the rod just before it strikes the table?
Решение
(III) Момент инерции стержня
относительно нижней точки I = mL2/3 (см.
решение задачи 40). Проще всего воспользоваться
законом сохранения механической энергии (сила
трения работы не совершает): 
Отсюда 
Непосредственно перед
падением верхний конец стержня имеет скорость 
36. (III) Оцените угловое ускорение руки и мышечную силу трицепса при броске шара массой 1 кг (см. рисунок к задаче 33). Известно, что шар ускоряется из состояния покоя до скорости 1 м/с за 0,22 с. Массу предплечья считать равной 3,4 кг и равномерно распределенной по его длине.
Assume that a 1.0-kg ball is thrown solely by the action of the forearm in Figure before rotating about the elbow joint under the action of the triceps muscle. The ball is accelerated from rest to 1.0 m/s in 0.22 s, at which point it is released. Calculate (a) the angular acceleration of the arm and (b) the force required of the triceps muscle. Assume the forearm has a mass of 3.4 kg and rotates like a uniform rod about an axis at its end.
Решение
Примем для предплечья модель
однородного стержня, вращающегося вокруг
неподвижной оси (локтевой сустав). Обозначим
расстояние от локтевого сустава до кисти через r1
= 30 см, расстояние от локтевого сустава до точки
крепления мышцы трицепса через r2 = 2,5 см,
массу шара через m1, массу предплечья через m2.
Среднее угловое ускорение 
Угловое смещение j = at2/2=0,363 рад = 21°. Сила мышцы F совершает работу A = Fjr2. Эта работа идет на увеличение кинетической энергии руки и шара:
Отсюда F = 117 Н.
37. (II) Метатель молота ускоряет молот массой 7,3 кг в течение четырех полных оборотов руки и бросает его со скоростью 27,2 м/с. Считая угловое ускорение постоянным, а радиус окружности равным 2 м, найдите: а) угловое ускорение молота; б) его тангенциальное ускорение; в) его центростремительное (радиальное) ускорение непосредственно перед броском; г) величину и направление силы (по отношению к радиусу кругового движения), с которой атлет действует на молот непосредственно перед броском. Действием силы тяжести пренебречь.
A hammer thrower accelerates the hammer (mass = 7.3 kg) from rest within four full turns (revolutions) and releases it at a speed of 27.2 m/s. Assuming a uniform rate of increase in angular velocity and a radius of 2.0 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force exerted on the hammer by the athlete just before release, and (e) the angle of this force with respect to the radius of the circular motion. Neglect the effect of gravity.
Решение
Линейное и угловое ускорения
соответственно равны: 
Отсюда находим время ускорения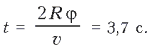 
Поэтому at = 7,4 м/с2; a = 3,7 рад/с2.
Непосредственно перед
броском радиальное ускорение 
Полная сила, с которой атлет
действует на молот: 
По отношению к радиусу эта
сила направлена под углом 
Продолжение. См. № 1, 5, 9, 13, 17, 21, 25/01