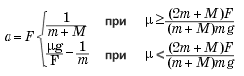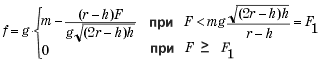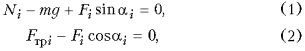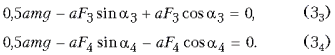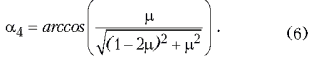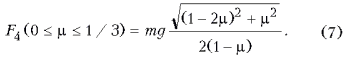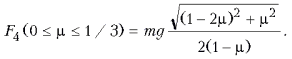Абитуриенту

В.А.Алешкевич, А.В.Грачев, Г.А.Миронова,
В.А.Погожев, М.В.Семенов, А.А.Якута

Вступительные экзамены по физике

В 2000 г. на физическом факультете Московского государственного университета имени М.В.Ломоносова проводилась в два тура олимпиада МГУ «Абитуриент-2000» (в марте и мае) и вступительный экзамен (в начале июля). Олимпиадные задания и экзаменационные билеты по физике содержали два теоретических вопроса, формулировки которых были взяты из программы по физике, опубликованной в справочнике для поступающих в МГУ, и две задачи. Абитуриенты, набравшие на олимпиаде по математике и физике в сумме не менее 13 баллов (максимальная оценка по физике – 10 баллов, математике – 5 баллов), были приглашены для учебы на факультете. Ниже приводятся условия предлагавшихся задач и их решения. В решениях особое внимание уделено обоснованию возможности применения того или иного физического закона и указаны предположения, в том числе и так называемые стандартные, которые необходимо было сделать в ходе решения.

По всем вопросам приема обращаться по телефону: 939-1241 (отдел по новому приему и работе со школьниками физического факультета МГУ).

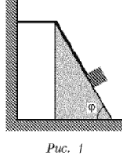• На полу около стены стоит гладкий клин. На его плоскости, образующей с горизонтом угол j,  лежит груз, удерживаемый невесомой нерастяжимой нитью. Один конец нити прикреплен к стене так, что участок нити между стеной и клином горизонтален. Остальная часть нити лежит на наклонной плоскости (рис. 1). Найдите зависимость от времени t скорости движения груза относительно пола после начала движения клина от стены с ускорением а, параллельным горизонтальному участку нити.

Решение

Из условия задачи ясно, что после начала движения клина (t = 0) груз будет двигаться по его поверхности лишь ограниченное время, а именно, вплоть до того момента t, когда точка крепления нити к грузу достигнет вершины клина. Поскольку иное специально не оговорено в условии задачи, будем 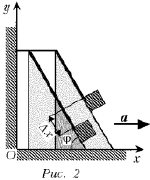считать, что клин движется поступательно, а нить к грузу прикреплена так, что последний при движении клина также движется поступательно. Именно в этих предположениях и будем искать ответ на вопрос задачи для промежутка времени 0 < t < t. Поскольку до момента времени t = 0 клин покоился, а затем его начали двигать с постоянным ускорением а, скорость клина относительно пола в момент времени t будет равна v(t) = at. Поэтому относительно неподвижной лабораторной системы координат, ось ОХ которой параллельна отрезку нити, не лежащему на клине, а ось ОY направлена вертикально вверх (рис. 2), клин за достаточно малый промежуток времени Dt переместится на расстояние Dx(t, t + Dt) = v_x(t)Dt = = atDt.

По условию задачи, нить следует считать нерастяжимой. Поэтому за указанное время длина отрезка нити, лежащего на клине, уменьшится на ту же величину Dx(t, t + Dt), и груз переместится по клину на то же самое расстояние. С помощью рис. 2 легко доказать, что проекция перемещения груза на ось ОХ за рассматриваемый промежуток времени равна

Dx_гр(t, t + Dt) = (1 – cos j)Dx(t, t + Dt) = (1 – cos j)atDt,

а на ось ОY –

Dy_гр(t, t + Dt) = Dx(t, t + Dt)sin j = atDtsin j.

По определению, v_грx(t) = Dx_гр(t, t + Dt)/Dt и v_грy(t) = Dy_гр(t, t + Dt)/Dt, отсюда для моментов времени 0 < t < t при сделанных выше предположениях составляющие скорости груза относительно пола равны

Dv_грx(t) = at(1 – cos j); Dv_грy(t) = atsin j,

а искомая величина скорости груза

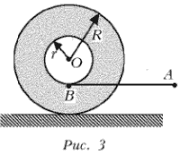
• На цилиндрическую часть катушки радиусом r, лежащей на столе, намотана легкая нерастяжимая нить, отрезок АВ которой горизонтален (рис. 3). В момент времени t = 0 точку нити А начинают тянуть с постоянным горизонтальным ускорением а. При этом катушка начинает катиться без проскальзывания так, что ее ось не изменяет своей ориентации. Через какое время длина горизонтального участка нити изменится в n раз, если длина отрезка АВ была равна L₀, а внешний радиус катушки равен R?

Решение

По условию задачи, при перемещении точки нити А катушка движется по плоскости, сохраняя ориентацию своей оси. Следовательно, считая, как это обычно и делается в подобных задачах, катушку твердым телом, ее движение можно представить как сумму поступательного движения со скоростью v₀, равной скорости движения оси катушки, и вращения с угловой скоростью w вокруг этой оси. Поскольку качение катушки происходит без проскальзывания, то w = v₀/R. Из сказанного следует, что в тот момент, когда скорость оси катушки равна v₀, скорость точки В должна быть равна

 а потому при движении катушки с течением времени длина отрезка нерастяжимой нити АВ должна уменьшаться.

Учитывая, что, по условию задачи, отрезок нити АВ остается горизонтальным, а первоначально покоившуюся точку А перемещают с постоянным ускорением а, коллинеарным нити, искомый промежуток времени t должен удовлетворять уравнению:

где – ускорение центра катушки. Из этих уравнений , и с учетом условия 0 і t интересующий промежуток времени равен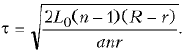

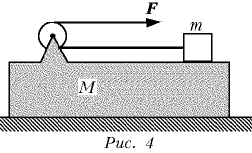• На гладком горизонтальном столе лежит доска массой М, а на ней находится груз массой m. К грузу прикреплена невесомая гладкая нерастяжимая нить, перекинутая через блок, закрепленный на доске. Свободный конец нити тянут с силой F так, как показано на рис. 4. При этом отрезки нити, не лежащие на блоке, горизонтальны, а вся нить располагается в одной вертикальной плоскости. Коэффициент трения груза о доску равен m. Найти ускорение груза относительно стола.

Решение

Будем решать задачу при следующих стандартных предположениях: действием воздуха на тела системы можно пренебречь, и лабораторную систему отсчета, относительно которой стол неподвижен, можно считать инерциальной. Кроме того, будем считать, что блок к доске и нить к грузу прикреплены так, что под действием силы F может возникнуть лишь поступательное движение этих тел. Поскольку нить является гладкой, то действующие со стороны нити на блок силы не могут иметь составляющей, направленной по касательной к блоку. Полагая, как обычно, что ось, вокруг которой мог бы вращаться блок, совпадает с его геометрической осью, можно утверждать, что при любом натяжении нити блок не будет вращаться. Поэтому, учитывая невесомость нити, можно утверждать, что величина силы натяжения во всех точках нити должна быть одинакова и равна величине приложенной к ее свободному концу силе F. Следовательно, на груз со стороны нити должна действовать сила, равная –F. Поскольку нить невесома, то сумма сил, действующих на нее, должна быть равна нулю, а потому, вспоминая третий закон Ньютона, можно утверждать, что со стороны нити на блок должна действовать сила 2F.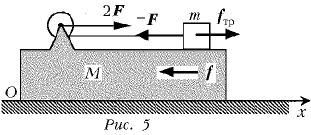

Из условия задачи ясно, что если движение груза по доске и может иметь место, то груз при этом будет двигаться по доске к блоку. Следовательно, сила трения fтр, действующая на груз со стороны доски, может быть направлена только так, как показано на рис. 5. На этом же рисунке показаны сила –F, действующая на груз со стороны нити, сила трения f = –f_тр, действующая на доску со стороны груза, и ось ОХ используемой при решении задачи лабораторной системы отсчета. Поскольку, по условию задачи, доска находится на гладкой горизонтальной поверхности и толщина доски постоянна, то уравнения движения груза и доски в проекциях на ось ОХ должны иметь вид:

ma_x = f_тр – F; MA_x = 2F – f_тр,

где а_х и А_х – проекции ускорений груза и доски на ось ОХ.

Учитывая, что груз при указанных условиях не движется по вертикали, на основании второго закона Ньютона можно утверждать, что величина N нормальной составляющей силы реакции доски на груз равна mg, где g – величина ускорения свободного падения. Тангенциальная же составляющая силы реакции доски на груз – сила сухого трения f_тр, – согласно закону Кулона–Амонтона, не может быть по модулю больше mN.

Очевидно, что при достаточно большом коэффициенте трения груз не будет скользить по доске. Поэтому его ускорение относительно доски будет равно нулю и, следовательно, a_x = A_x. В этом случае, складывая приведенные выше уравнения движения груза и доски, получим

 

Поскольку при этом сила сухого трения является силой сухого трения покоя, то ее величина не может превышать своего максимального значения, т.е. f_тр Ј mmg. Из сказанного следует, что груз не будет скользить по доске, если

Если же m < m_min, то, полагая, как обычно, величину коэффициента трения скольжения не зависящей от скорости скольжения и равной максимальному значению коэффициента трения покоя, из приведенных выше соотношений получим a_x = mg – F/m. Итак, при выполнении сделанных предположений искомое ускорение груза относительно стола равно

• В системе, показанной на рис. 6, грузы массами m₁ и m₃ прикреплены к концам невесомой нерастяжимой нити. 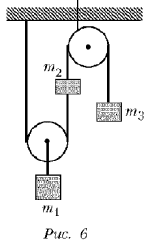На такой же нити, один конец которой закреплен, а другой прикреплен к грузу массой m₂, висит подвижный блок. К оси этого блока на легких нерастяжимых нитях подвешен груз массой m₁. Отрезки нитей, не лежащие на блоках, вертикальны. Пренебрегая трением и массой блоков, найдите ускорение груза m₁.

Решение

При решении задачи будем, как обычно, пренебрегать влиянием воздуха на движение тел системы и считать лабораторную систему, относительно которой покоится ось неподвижного блока, инерциальной. Поскольку отрезки нитей, не лежащие на блоках, вертикальны и действующие на грузы силы тяжести направлены вертикально, можно утверждать, что и ускорения грузов должны быть направлены вертикально. Если использовать обозначения, показанные на рис. 7, то, учитывая, что, по условию задачи, нити являются нерастяжимыми, и считая блоки идеальными цилиндрами, вращающимися вокруг своих геометрических осей, можно утверждать, что координаты грузов должны удовлетворять соотношениям:

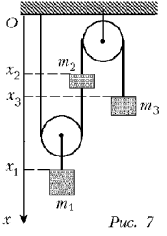2x₁(t) – x₂(t) = C₁;

x₂(t) + x₃(t) = C₂,

где С₁ и С₂ – постоянные величины, определяемые длиной нитей и радиусами блоков. Из этих соотношений следует, что проекции ускорений грузов на ось ОХ не являются независимыми и подчиняются соотношению 2a_x1 = a_x2 = –a_x3.

Поскольку, по условию задачи, нити являются невесомыми, а массой блоков и трением в их осях следует пренебречь, то величина силы натяжения нити, перекинутой через подвижный блок, в любом ее сечении должна быть неизменной, как и величина силы натяжения второй нити, перекинутой через неподвижный блок. Если величину силы натяжения первой нити обозначить F₁, а второй F₂, то на основании второго закона Ньютона можно утверждать, что уравнения движения грузов в проекциях на ось выбранной лабораторной системы отсчета должны иметь вид:

m₁a_x1 = m₁g – 2F₁; m₂a_x2 = m₂g + F₁ – F₂;

m₃a_x3 = m₃g – F₂,

где g – величина ускорения свободного падения. Умножив последние два уравнения почленно на 2 и –2 соответственно, а затем сложив их с уравнением движения первого груза, с учетом полученного ранее соотношения между ускорениями грузов определим искомое ускорение первого груза:

 

•  Твердый шар радиусом r и массой m лежит на полу, касаясь вертикальной стены. К нему прижимают с силой F, направленной горизонтально, брусок высотой h < r так, как показано на рис. 8. Пренебрегая трением, найдите силу давления f шара на пол.

Решение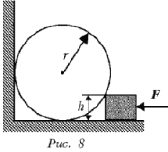

Поскольку шар и брусок, по условию задачи, следует считать гладкими, то действующие на эти тела силы реакции опор могут иметь лишь составляющие, направленные по нормалям к границам в точках их соприкосновения с другими телами.

Обозначим силы, действующие на шар со стороны пола и со стороны бруска, n и N соответственно. Как обычно, будем считать инерциальной лабораторную систему, относительно которой пол и стена неподвижны, и пренебрежем влиянием воздуха на рассматриваемые тела.

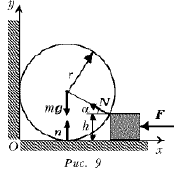Тогда с учетом обозначений, приведенных на рис. 9, на основании второго и третьего законов Ньютона можно утверждать, что шар и брусок могут оставаться неподвижными, если

где g – величина ускорения свободного падения.

Обратившись вновь к рис. 9, можно доказать, что вплоть до момента отрыва шара от пола величина угла a должна удовлетворять соотношению а потому

В условии задачи специально не оговорено, что между шаром и полом существуют силы притяжения. Поэтому можно утверждать, что при наличии контакта шара с полом возможные значения нормальной составляющей силы реакции пола на шар должны удовлетворять условию n_y > 0. Следовательно, при наличии контакта шара с полом действующая на брусок сила не может превышать определенного значения, а именно, ее величина должна удовлетворять неравенству

Учитывая, что, согласно третьему закону Ньютона, искомая сила f давления шара на пол должна быть равна –n, получим

•  На горизонтальной крышке стола лежит однородный куб массой m, к середине верхнего ребра которого прикреплена легкая нить. Коэффициент трения куба о крышку равен m, причем m < 0,5. С какой минимальной силой и в каком направлении нужно тянуть за нить, чтобы куб начал опрокидываться без скольжения?

Решение

При решении задачи будем полагать, что крышка стола покоится относительно инерциальной системы отсчета, куб и крышка являются твердыми телами и можно пренебречь действием воздуха. По условию задачи, под действием приложенной к нити силы куб должен начать поворачиваться без скольжения. 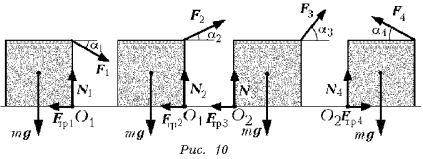Поскольку нить прикреплена к середине одного из верхних горизонтальных ребер и ее тянут перпендикулярно этому ребру, из соображений симметрии можно утверждать, что куб должен начать поворачиваться вокруг одного из нижних ребер, параллельных тому ребру, к середине которого прикреплена нить. На рис. 10 показаны сечения куба вертикальной плоскостью, в которой располагается нить. Здесь же показаны силы, действующие на куб, когда за нить тянут вниз или вверх под углом a_i к горизонту с силой F_i такой, что при ее незначительном увеличении куб начинает поворачиваться. В первом случае угол наклона нити к горизонту a₁ будем считать отрицательным, а во всех остальных – положительным, причем Поскольку куб является однородным, действующая на него сила тяжести mg (где g – ускорение свободного падения) приложена к центру куба. Результирующая сил реакции крышки, как это обычно и делают, изображена в виде двух составляющих: нормальной N_i и тангенциальной F_трi. Точки приложения этих составляющих в первом и втором случаях обозначены на рис. 10 символом О₁, а в третьем и четвертом – О₂.

Поскольку куб не должен скользить по крышке, при сделанных выше предположениях и с учетом соглашения о правиле знаков при отсчете угла наклона нити к горизонту, согласно первому закону Ньютона должны выполняться равенства:

где i = 1, 2, 3, 4.

Поскольку при незначительном увеличении силы, действующей на куб со стороны нити, он начинает поворачиваться, то алгебраическая сумма моментов сил в рассматриваемых случаях должна быть равна нулю. Поэтому в первом и втором случаях, выбирая в качестве оси вращения ребро куба, проходящее через точку О₁, и вспоминая определение момента силы относительно данной оси, в соответствии со сказанным получим:

где i = 1, 2. В третьем и четвертом случаях из сказанного ранее следует, что

Во всех случаях, согласно закону Кулона, величина тангенциальной составляющей силы реакции крышки – силы сухого трения покоя – не может превышать произведения коэффициента трения на величину нормальной составляющей силы реакции опоры, т.е. должно соблюдаться неравенство

Из уравнений (3_1,2) следует, что величина силы натяжения нити в первом и втором случаях должна быть равна причем, согласно уравнениям (1), (2) из неравенства (4) в этих случаях Поскольку по условию задачи m < 0,5, то tg a_i < 0. Учитывая, что в первом случае , а во втором случае , можно утверждать, что второй случай при заданных условиях не реализуется, а в первом случае и, следовательно,

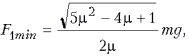
причем

В третьем случае что следует из (3₃), а из соотношений (1), (2) и (4) вытекает, что Следовательно, этот случай может иметь место, причем

и нить следует тянуть вертикально вверх.

Наконец, в четвертом случае из уравнения (3₄) получим

причем из соотношений (1), (2) и (4) следует, что

Поскольку максимального значения синус угла достигает тогда, когда угол становится равным p/2, то искомая величина силы натяжения нити минимальна при a₄ = p/4 и равна

Конечно, это утверждение будет верно, если при этом выполняется соотношение (5_4а), т.е. имеет место неравенство .

Если же то нить следует тянуть под углом

При этом искомая сила натяжения нити должна быть равна

Итак, при нить следует тянуть так, как показано на рис. 10, под углом к горизонту, определяющимся формулой (6), с силой

 

Если же 1/3 Ј m Ј 0,5, то к нити следует прикладывать силу, направленную под углом a₄ = p/4 к горизонту, величина которой не превышает указанное выше значение и равна

 

Продолжение следует