«Проблема времени» в физике

«Проблема времени» появилась в результате попыток ответить на вопрос: «Что такое время?» На первый взгляд, этот вопрос кажется простым. Вся наша жизнь и деятельность происходит во времени. Мы осознае1м его течение в череде событий дня, в смене дней и ночей, в регулярной последовательности времен года. Измеряют время с помощью периодических явлений природы. Так, эталон года равен промежутку времени между двумя последовательными прохождениями центра видимого диска Солнца через точку весеннего равноденствия. Эталоном суток является период вращения Земли вокруг собственной оси. Это вращение наблюдают как суточное обращение звездного небосвода вокруг Земли. Современный эталон секунды - атомная секунда - был принят в 1967 г. на XIII Международной конференции по мерам и весам. Он вводится с помощью генератора высокочастотных колебаний, в котором используются колебания атомов цезия-133. Одна атомная секунда равна интервалу времени, за который происходит 9 192 631 700 таких колебаний. Колебания фиксируются как радиоизлучение длиной волны около 3,26 см.

В физике метод измерения определяет физическую величину. Например, ускорение есть физическая величина, характеризующая изменение скорости в единицу времени. При таком подходе время следует определить как математическую величину, которую используют для измерения длительности событий. Видимо, поэтому древнегреческий философ и математик Платон (427-347 гг. до н.э.) рассматривал время как математический образ вечности, ведь интервалы времени - сутки и год - остаются всегда неизменными.

Однако под одним и тем же звездным небом происходят самые разные события. Мы точно знаем, что наш вчерашний день отличается от настоящего, а на будущий день мы планируем новые дела и ждем новых событий. Понятия «прошлое», «настоящее» и «будущее» являются качественными характеристиками событий. Они отражают главное свойство времени: оно всегда неумолимо изменяется от прошлого к будущему.

Знаменитый ученик Платона Аристотель (384-322 гг. до н.э.) считал, что деление времени на прошлое и будущее происходит только в душе человека. В космосе все интервалы времени равноправны, причем моменты прошлого и будущего не существуют, реально только одно мгновение настоящего. Это представление следовало из опыта астрологических предсказаний, которые были частью культуры эпохи Аристотеля. Астрологи, используя одни и те же перемещения небесных светил, предсказывали разное будущее разным людям.

Таким образом, уже в эпоху античности появилось интуитивное представление об абсолютном времени, которое связывали с движением вечного и неизменного для всех звездного неба, и об относительном времени, которое образуют моменты времени, фиксирующие события прошлого, настоящего и будущего каждого отдельного человека. «Проблема времени» состоит в том, чтобы объяснить существование относительного времени и найти причины необратимой последовательности событий от прошлого к будущему.

Интерес к этой проблеме сохранялся в течение многих веков. Исторически сложилось так, что относительное время стало рассматриваться как результат деятельности души. Например, знаменитый средневековый богослов Блаженный Августин писал: «В тебе, душа моя, измеряю я времена … и когда измеряю их, то измеряю не самые предметы, которые проходили и прошли уже безвозвратно, а те впечатления, которые они произвели на тебя». Понятно, что такой способ измерения времени не подходит для количественного описания движения тел. Поэтому физики и математики второй половины XVII в. использовали абсолютное время. Именно его существование постулировал Исаак Ньютон в «Математических началах натуральной философии» (1687 г.). Он определил его как «абсолютное, истинное, математическое...», причем оно «без всякого отношения к чему-либо внешнему протекает равномерно и иначе называется длительностью». Это определение времени отражено в структуре второго закона динамики Ньютона. Математическая запись этого закона не изменяется, если изменить знак времени t на -t, т.е. обратить абсолютное время t вспять. Принято говорить, что динамика Ньютона симметрична по абсолютному времени.

Однако элементарное сознательное восприятие времени - поток, или перемещение момента «теперь» в будущее, - не имеет места в физическом описании реального мира, и это является одной из наиболее непостижимых загадок физики. Совершенно не ясно, является ли это недостатком тех физических теорий, которые нам известны, или же ощущение течения времени представляет собой иллюзию. Таким образом, объяснение происхождения «стрелы времени» есть важнейшая проблема физики.

Симметрия по абсолютному времени связана с фундаментальным свойством нашего мира. В 1918 г. математик Э.Нётер доказала очень важную теорему. Из нее следует, что если уравнение движения тела симметрично по времени, то полная энергия тела сохраняется, т.е. не зависит от времени. Поэтому, используя только полную энергию какой-либо системы, нельзя ввести различие между прошлым и будущим.

Однако это можно сделать, если движение системы неустойчиво. В качестве примера рассмотрим движение обычного маятника. Пусть грузик, висящий на нерастяжимой нити, может двигаться в вертикальной плоскости (рис. 1).

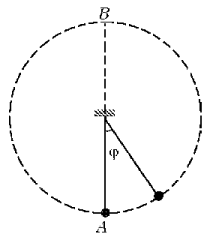
Рис. 1. Математический маятник

Мы будем пренебрегать как размерами грузика, так и любыми диссипативными процессами - трением в точке подвеса, сопротивлением воздуха и т.п. В этом случае маятник называют математическим. Его полная энергия сохраняется и равна

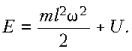
Здесь m - масса грузика, l - длина нерастяжимой нити, w - угловая скорость. Маятник гравитационно взаимодействует с массой Земли, и его потенциальная энергия равна U = mgl(1 - cos j), где g - ускорение силы тяжести, j - угол отклонения маятника. Период колебаний маятника Т₀ зависит, вообще говоря, от максимального значения угла отклонения j₀.

Если то

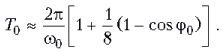
Для качественного анализа типов энергетических состояний маятника физики используют фазовый портрет. Так называют геометрическую картину, на которой изображена зависимость импульса маятника p = ml²w от угла j. Фазовый портрет можно нарисовать, зная только полную энергию Е. Он показан на рис. 2.

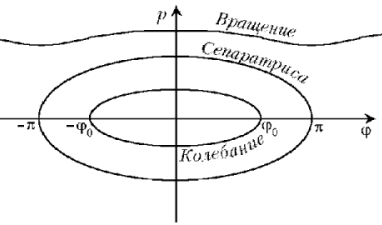
Рис. 2. Фазовый портрет маятника

Если Е < 2mgl, то угол отклонения j < p/2, и маятник совершает колебания относительно точки А. Эти колебания устойчивы, т.к. при любом малом внешнем ударе, т.е. при небольшом изменении полной энергии, маятник сохранит колебательный тип движения, хотя амплитуда колебаний слегка изменится.Фазовая кривая колебаний замкнута и при небольших j₀ является эллипсом. Если Е > 2mgl, грузик будет совершать вращения. Им отвечает линия, похожая на косинусоиду. Состояние вращения тоже устойчиво. Если движение маятника устойчиво, то качественные характеристики этого движения, будь то колебания или вращения, одинаковы для всех моментов времени. Образно говоря, во все моменты времени маятник повторяет сам себя, и у него нет ни прошлого, ни будущего.

Если Е = 2mgl, то маятнику хватает энергии лишь для того, чтобы достичь самой верхней точки В. Фазовую траекторию в этом случае называют сепаратрисой - линией, которая делит фазовую плоскость на две области: область вращений и область колебаний.

Из опыта мы знаем, что положение маятника в точке В неустойчиво, т.к. при любом малом внешнем воздействии маятник из этого положения выйдет и начнет падать в нижнее положение. Если уменьшить энергию маятника, он будет колебаться и уже не достигнет точки В. Если же его энергию увеличить, то он будет вращаться и проходить точку В, не останавливаясь. Таким образом, движение по сепаратрисе или вблизи нее неустойчиво. Это свойство неустойчивости движения позволяет ввести понятия прошлого и будущего для маятника. Например, пусть маятник совершает колебания вблизи сепаратрисы и его энергия равна Е₁ =  2mgl - dE, где dE n mgl. В момент времени t₀ грузик получает слабый толчок, и его энергия становится равной E₂ = 2mgl + dE.
Энергия толчка равна Е₂ - Е₁ =   2(dЕ) n 2mgl. В результате при t > t₀ маятник уже будет вращаться. В момент t₀ произошло событие, толчок, которое качественно изменило состояние движения маятника: он перешел от колебаний к вращениям. Поэтому время t < t₀ до толчка можно назвать прошлым, момент t₀ - настоящим, а время после толчка t > t₀ - будущим. Подчеркнем, что благодаря неустойчивости состояние маятника изменилось необратимо, т.е. сам по себе он не вернется в свое прошлое, т.е. в колебательное состояние. Для такого перехода необходимо внешнее воздействие.

Понятие неустойчивости фазовых траекторий было введено русским математиком Софьей Ковалевской в 1889 г. в работе, посвященной математической модели колец Сатурна. Затем, в начале 90-х гг. XIX в. русский математик Александр Ляпунов начал развивать оригинальную теорию устойчивости движений динамических систем.

Вопросы неустойчивости и устойчивости фазовых траекторий привлекли внимание великого математика и физика Анри Пуанкаре. В 1892 г. он предложил гипотезу о связи неустойчивости состояния физической системы и необратимого течения времени от прошлого к будущему. Пуанкаре полагал, что если система находится в неустойчивом состоянии, то малые внешние воздействия могут переводить ее в качественно различные состояния. Например, от одномерных колебаний к двумерным или трехмерным (рис. 3), от вращений по  окружности к движению по сложным замкнутым поверхностям (рис. 4). Если эти переходы происходят быстро, то поведение системы похоже на хаотичное. Возврат в начальное неустойчивое состояние практически невозможен. Опыт показывает, что попасть в хао-тичное состояние легче, чем выйти из него.

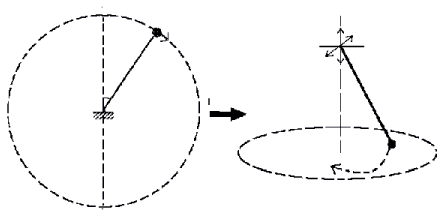
Рис. 3. Переход от одномерных колебаний маятника с неподвижной точкой подвеса к трехмерным колебаниям маятника с подвижной точкой подвеса

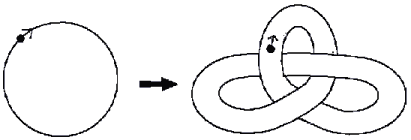
Рис. 4. Переход от вращения по окружности к трехмерному движению по сложной замкнутой поверхности

Современники Пуанкаре не заметили его гипотезы. Она не была подкреплена математическим анализом. Для понимания неустойчивых движений еще не пришло время: не был достаточно развит аппарат теории вероятностей, и не было еще тщательных физических экспериментов, связанных с изучением турбулентных потоков в жидкостях и газах.

На рубеже XIX-XX вв. был создан математический аппарат молекулярно-кинетической теории термодинамических процессов в разреженных газах. Это произошло благодаря усилиям многих физиков-теоретиков, но больше всего для утверждения атомистики в физике сделал выдающийся немецкий физик Людвиг Больцман.

Больцман предложил динамическое объяснение законов термодинамики. Первый закон гласит: сумма подведенной к системе теплоты и работы, совершенной над системой, равна возрастанию внутренней энергии системы. Другими словами, энергия изолированной системы сохраняется, если принять, что теплота и работа есть формы кинетической энергии молекул.

Второй закон термодинамики устанавливает наличие в природе однонаправленности всех процессов. Например, горячие тела с течением времени охлаждаются, прыгающий мяч в конце концов останавливается. Здесь проявляется то свойство природы, которое Рудольф Клаузиус еще в 1850 г. сумел отделить от закона сохранения энергии. Это свойство состоит в том, что, хотя полное количество энергии должно сохраняться в любом процессе, распределение этой энергии по возможным состояниям термодинамической системы изменяется необратимым образом. Например, остывшее тело не может стать само по себе горячим, часть его тепла передана окружающей среде.

Второй закон термодинамики указывает естественное направление, в котором происходит изменение распределения энергии, причем это направление совершенно не зависит от общего количества энергии. Как понял Клаузиус, в любой изолированной системе все процессы идут так, что число способов распределить внутреннюю энергию по составляющим систему молекулам либо не изменяется, либо возрастает. Причем если в систему поступает теплота DQ при температуре Т, то число способов распределить внутреннюю энергию возрастает на величину DN, которая пропорциональна величине DS = DQ/T. Величину S Клаузиус назвал энтропией и записал в 1865 г. второй закон термодинамики для изолированных систем в виде: DS і 0. Таким образом, согласно Клаузиусу, энтропия изолированной системы никогда не уменьшается, и второй закон термодинамики «самый верный из всех известных нам опытных законов, он вернее смерти, так как смерть - только частный случай второго начала».

Строгое определение энтропии достаточно сложно, однако ей можно дать ряд интуитивно понятных физических толкований. Так, энтропию можно рассматривать как меру беспорядка. Если система имеет четко выраженную структуру и в ней царит порядок, то ее энтропия мала. Напротив, системы с высокой энтропией беспорядочны и хаотичны. Например, система, состоящая из расположенных рядом холодного и горячего тел, обладает более низкой энропией, чем аналогичная система, в которой оба тела находятся в равновесии и имеют одинаковую температуру. Дело в том, что система более упорядочена в тепловом отношении, если теплота сосредоточена главным образом в горячем теле, чем если ее распределить равномерно по всей системе. Иначе говоря, в первом случае система более организована.

Состояние равновесия можно отождествить с состоянием, когда энтропия максимальна. При любых изменениях изолированной системы ее энтропия возрастает. Когда же система достигает наконец равновесия, энтропия больше не увеличиватся - она достигла своего максимума.

Энтропию можно также связать с информацией. Когда система находится в высокоупорядоченном состоянии с малой энтропией, для ее описания требуется много информации. В беспорядочной системе с большой энтро-пией содержится мало информации. Обычно приводимый пример – текст, который вы сейчас читаете. Когда буквы алфавита специально расставлены в должном порядке, текст несет информацию в виде слов и т.д. Если рассыпать набор и перемешать все буквы, количество информации станет существенно меньше. Вывод: информацию можно отождествить с отрицательной энтропией, или, как иногда говорят, негаэнтропией. Когда энтропия растет, информация утрачивается.

В 1866 г. двадцатидвухлетний Больцман поставил перед собой задачу: дать молекулярно-кинетическое обоснование необратимого роста энтропии в нашем мире. Для достижения этой цели ему потребовалось около сорока лет. В результате были созданы основы статис-тической механики и получена математическая формулировка гипотезы молекулярного хаоса. Эта гипотеза обсуждалась еще греческими атомистами Эпикуром и Демокритом, которые полагали, что материя состоит из маленьких частиц, находящихся в непрестанном хаотическом движении. Если ограниченный объем газа находится в состоянии молекулярного хаоса, то в любой точке объема может находиться любая молекула с любой скоростью. В этом случае распределение молекул по скоростям описывается функцией Максвелла-Больцмана.

Согласно Больцману молекулярный хаос нельзя уничтожить, т.е. движение материи имеет вероятностную природу. Он показал, что в молекулярном хаосе число способов распределить энергию максимально. Тогда из второго закона термодинамики следует, что направление всех природных процессов таково, что любые упорядоченные структуры должны разрушаться и переходить в хаотическое состояние. Следующим шагом в рассуждениях Больцмана было введение направления течения времени: время течет в направлении роста энтропии. Переходы в состояние молекулярного хаоса создают время. Полное разрушение упорядоченных структур ассоциируется со смертью. Поэтому направление времени, введенное Больцманом, - это направление к смерти Вселенной.

Однако и наш повседневный опыт, и астрономические наблюдения свидетельствуют о том, что наряду с процессами разрушения структур, выравнивания температур и концентраций веществ идут разнообразные процессы самоорганизации материи. Как раз благодаря самоорганизации существуют все удивительные формы жизни, имеющие очень высокую степень упорядоченности. Получается, что либо самоорганизующиеся системы не подчиняются закону роста энтропии и не чувствуют больцмановского времени, либо увеличение энтропии не всегда сопровождается переходом всей системы к полному хаосу.

В первом случае фактически предполагается, что самоорганизующиеся системы - живые организмы - принципиально отличаются от всего остального мира и, возможно, даже не подчиняются физическим законам. Именно такую идею предложил в начале 80-х гг. ХХ в. лауреат Нобелевской премии биофизик И.Пригожин. Он исходил из того факта, что живая материя отличается от неживой своей способностью изменяться. Любой организм растет, изменяется его форма, появляются новые функции, позволяющие более комфортно существовать в природе. Эту способность еще Аристотель назвал самоорганизацией. Именно благодаря самоорганизации живая материя эволюционирует от простых организмов к существам со сложной нервной системой. Пригожин считает, что необходимо создавать новую физику живых систем.

Так ли это? Можно ли понять явление самоорганизации, используя известные физические законы? Ответ на этот вопрос скорее всего утвердительный. Действительно, ведь явления самоорганизации известны и в неживой природе. Самый яркий в буквальном смысле пример - это Солнце, наше дневное светило. Солнце как структура существует благодаря балансу между электромагнитным и гравитационном взаимодействиями. Тяготение всей массы Солнца сжимает его вещество до плотностей порядка 10⁵ кг/см³. В этом случае среднее расстояние между частицами оказывается меньше характерного размера атома водорода (10-10 м). Поэтому в недрах Солнца атомов нет, а вещество представляет собой плазму - горячий газ из протонов и электронов. Плазма в целом электрически нейтральна, но ее давление определяется кулоновским отталкиванием электронов. Это связано с тем, что масса электрона примерно в тысячу раз меньше массы протона. В однородно нагретой плазме средняя кинетическая энергия электронов и протонов одинакова, но их средние скорости различны из-за различия масс. Электроны движутся быстрее протонов и поэтому чаще встречаются и обмениваются импульсами друг с другом, а не с протонами. Обмен импульсами происходит за счет электромагнитного взаимодействия электронов, и именно этот обмен создает давление плазмы.

В Солнце давление плазмы уравновешивается тяготением суммарной массы протонов. Это равновесие имеет статистический характер и выполняется в среднем по объему Солнца. Для подобных систем справедлива теорема вириала, впервые сформулированная и доказанная Клаузиусом. Согласно этой теореме в изолированной системе суммарная внутренняя энергия движения частиц системы Е и энергия их взаимодействия U связаны соотношением 2Е + U = 0. Применяя эту теорему к солнечной плазме, следует считать U гравитационной энергией массы плазмы. Эта энергия отрицательна: U < 0. Суммарная кинетическая энергия частиц плазмы Е > 0. Полная энергия Солнца 1 = Е + U = -E. Полная энергия отрицательна: 1 < 0, как и должно быть для равновесной изолированной системы, состоящей из большого числа частиц, которые удерживаются вместе гравитационным притяжением.

В недрах Солнца, на глубине больше 200 тыс км, температура плазмы достигает 10 млн градусов. При таких температурах становится возможным протекание термоядерных реакций горения водорода - протон-протонный цикл. Благодаря им на Солнце из водорода образуется гелий и рождаются фотоны. Эти фотоны постепенно уходят из недр Солнца, достигают его поверхности и затем излучаются в космическое пространство – Солнце излучает часть своей энергии D1. Путешествуя из недр Солнца к его поверхности, фотоны из g-квантов превращаются в оптические и часть своей энергии отдают плазме. Плазма нагревается, и ее тепловая энергия Е увеличивается. Нагрев происходит медленно: за год температура солнечных недр изменяется менее чем на одну сотую градуса. Поэтому можно считать, что нагрев не нарушает вириального равновесия Солнца. В этом случае изменение полной энергии Солнца, несмотря на нагрев плазмы, будет отрицательным, т.к. D1 = -DE < 0 при DE > 0. Тогда изменение энтропии недр Солнца, согласно формуле Клаузиуса, равно DS = D1/Т = -DЕ/Т < 0. Таким образом, в ходе эволюции Солнца его энтропия убывает!

Убыль энтропии означает, что на хаотичное движение частиц плазмы накладывается упорядоченное движение типа конвективных потоков. Образно говоря, Солнце, сжигая свою массу, самоорганизует свое внутреннее строение, переходя от хаотичных микроскопи-ческих движений к крупномасштабным упорядоченным конвективным движениям.

Заметим, что у замкнутой системы Солнце + его излучение энтропия растет. Действительно, энтропия излучения пропорциональна объему, в котором оно находится. Для излучения, покидающего Солнце, этот объем растет. Таким образом, второе начало термодинамики в рассматриваемом случае выполняется. Однако полной хаотизации системы не происходит: недра Солнца самоорганизуются, а его излучение переходит в хаотичное состояние. Этот пример свидетельствует о том, что рост энтропии не всегда сопровождается тепловой смертью.

Самоорганизация Солнца происходит благодаря гравитационному взаимодействию всех частиц плазмы, т.е. она является результатом коллективного взаимодействия.

Вернемся к гипотезе Больцмана о времени. Она включает в себя два предположения. Во-первых, рост энтропии означает переход системы частиц в состояние молекулярного хаоса. Во-вторых, молекулярный хаос является наиболее вероятным и естественным состоянием материи.

Первое предположение, вообще говоря, неверно для систем, в которых существенную роль играет гравитационное взаимодействие. Это понятно из описанных выше некоторых свойств Солнца.

Второе предположение сыграло огромную роль при создании квантовой теории материи. Макс Планк использовал его в 1900 г. в работе, посвященной анализу свойств излучения абсолютно черного тела. В квантовой механике принят постулат о вероятностной природе движения материи.

Больцман был твердо убежден в существовании молекул и полагал, что хаотичность движения является их фундаментальным свойством и не связана с какими-либо взаимодействиями. Именно эта хаотичность и приводит к тому, что в результате столкновений устанавливается равновесное распределение молекул в идеальном газе.

Эти представления Больцмана использовали творцы квантовой теории материи, принимая постулат о вероятностной природе материи. Согласно этому постулату все события носят вероятностный характер и любое событие может повториться с абсолютной точностью. Например, элементарные частицы, в каких бы ядерных процессах они ни появлялись, всегда имеют один и тот же набор фундаментальных параметров. Так, электрон рождается всегда с одной и той же массой, с одним и тем же электрическим зарядом и с одной и той же из двух возможных проекций спина. При всем разнообразии элементарных частиц общим для них является то, что они сохраняют свою идентичность всегда. Поэтому только с их помощью нельзя отличить прошлое состояние системы от будущего. Электрон, существовавший сто лет назад, не отличается от наблюдаемого сегодня электрона или электрона, который будет существовать через сто лет. Отсюда следует, что в квантовой механике, созданной для описания микромира, не существует времени как последовательности неповторимых событий.

Таким образом, гипотеза о молекулярном хаосе, вообще говоря, не помогает решить «проблему времени». Следует отметить, что эта гипотеза помогла Больцману найти для идеального газа функцию, которая зависит от типа распределения молекул по скоростям и всегда растет при переходе от неравновесного распределения к равновесному. Эту функцию называют теперь энтропией по Больцману. Качественный смысл ее в следующем. Пусть есть объем газа, и суммарная кинетическая энергия молекул равна Е. Эту энергию можно распределять разными способами по молекулам. В равновесном газе число способов распределить конечную энергию Е бесконечно, т.к. любая молекула может иметь любую кинетическую энергию из интервала от 0 до Е, а число точек в этом интервале бесконечно.

В неравновесном газе каждая молекула имеет определенную энергию. Если молекулы одинаковые, то одному и тому же неравновесному состоянию может соответствовать N способов распределения энергии Е по молекулам. Каждое такое распределение называют состоянием системы: число N равно числу состояний, допустимых при заданной энергии. Энтропия по Больцману равна S = klnN, где k - постоянная Больцмана. При переходе от неравновесного состояния к равновесному число состояний N растет, соответственно растет и энтропия. В качестве примера рассмотрим ламинарное и турбулентное течения жидкостей. При подсчете больцмановской энтропии для ламинарного потока надо рассмотреть, как распределяется внутренняя энергия по молекулам. В турбулентном потоке струйки жидкости перемешиваются. Внешне беспорядка больше, чем в ламинарном потоке, но энергия распределяется по турбулентным вихрям, которые состоят из громадного числа молекул. Число вихрей гораздо меньше, чем число молекул. Энергия в турбулентном потоке распределяется меньшим числом способов, чем в ламинарном, – соответственно энтропия по Больцману ламинарного потока больше, чем энтропия турбулентного.

Итак, к концу XIX в. в теоретической физике появилось два определения энтропии - энтропия по Клаузиусу и энтропия по Больцману.

Энтропия по Клаузиусу характеризует способность газа перераспределять поступающую извне тепловую энергию. Чем больше тепла поглощается, тем больше изменение энтропии. Энтропию по Клаузиусу можно измерить.

Энтропия по Больцману не является наблюдаемой величиной. Дело в том, что, во-первых, любой реальный объем газа состоит из огромного числа частиц. Поэтому выполнить наблюдения координат и скоростей всех молекул, определив тем самым состояние системы, практически невозможно. Во-вторых, согласно гипотезе молекулярного хаоса координаты и скорость каждой молекулы изменяются случайным образом и независимо друг от друга. В этом случае каждому значению координаты молекулы отвечает бесконечное число возможных значений ее скорости. Это означает, что наблюдать конкретное состояние системы как совокупность определенных значений координат и скоростей молекул не только трудно, но и принципиально невозможно, если верна гипотеза молекулярного хаоса. Таким образом, число N можно только вычислить теоретически и нельзя проверить экспериментально. Соответственно энтропия по Больцману оказывается только теоретической величиной, которая может и не совпадать с энтропией по Клаузиусу. Этот факт стимулировал поток критических замечаний со стороны физиков и философов, живших в эпоху Больцмана. Замечания касались как самой гипотезы, так и математических расчетов Больцмана. Больцман воспринял эти замечания крайне эмоционально, страдая от насмешек и непонимания коллег. Возможно, именно эти страдания способствовали развитию у него депрессии и сильных головных болей. В результате 5 сентября 1906 г. Больцман покончил с собой.

Трагедией Больцмана было то, что он не дожил до полного признания своих идей всего нескольких месяцев, когда их активно начали использовать Эренфест, Смолуховский, Эйнштейн, Зоммерфельд.

Вопрос о связи энтропий по Больцману и по Клаузиусу остается актуальным до сих пор. Когда их можно отождествить? Ответ на этот вопрос нашел в 1947 г. физик Николай Крылов. Он выполнил несколько работ, посвященных динамическому обоснованию статистической механики. Крылов показал, что газ, состоящий из точечных частиц (модель абсолютно упругих молекул) и находящийся в ограниченном объеме, переходит из любого состояния в состояние молекулярного хаоса только благодаря столкновениям частиц. Для этого достаточно выполнения закона сохранения импульса при столкновениях и релятивистского соотношения 1² = (pc)² + (mc²)² между энергией 1, импульсом р и массой m любой молекулы. Оказывается, в этом случае траектория любой частицы неустойчива, и любое столкновение изменяет эту траекторию необратимым образом. Поэтому, даже если в начальный момент все частицы имели одинаковые импульсы и были сосредоточены в небольшой части объема, с течением времени каждая частица сможет побывать в любой части объема, ее импульс будет изменяться во всех направлениях, а его величина пробегать все доступные значения. В результате благодаря столкновениям в газе установится статистическое равновесие частиц, аналогичное распределению Максвелла. Как известно, закон сохранения импульса есть следствие однородности пространства. Кроме того, в частной теории относительности доказывается, что связь между 1, р и m есть следствие однородности и изотропии пространства, однородности времени и постоянства скорости света в вакууме. Поэтому результат Крылова о неизбежности перехода газа точечных частиц в состояние молекулярного хаоса является следствием свойств пространства и времени, а также ограниченности максимальной скорости распространения взаимодействий.

Таким образом, совсем не обязательно принимать постулат о молекулярном хаосе. Для появления хаотичного состояния необходимо, чтобы, во-первых, движения частиц были неустойчивыми, и во-вторых, эти частицы сталкивались или взаимодействовали друг с другом. Это взаимодействие называют внутренним. Оно только перераспределяет энергию внутри системы и является коллективным взаимодействием частиц.

Крылов показал, что для газа точечных частиц энтропии по Клаузиусу и по Больцману совпадают. Каждую из них можно выразить через среднее время свободного пробега частиц (между двумя последовательными столкновениями). Чем меньше время свободного пробега, тем больше энтропия. Определенная таким образом энтропия становится измеримой величиной, т.к. она зависит от характера внутреннего взаимодействия. Поэтому ее называют динамической энтропией.

Рост динамической энтропии не обязательно связан с переходом к равновесному распределению. Например, если столкновения частиц будут неупругими, то закон сохранения импульса не будет выполняться. В этом случае в системе появляется согласованное движение частиц, т.е. они образуют упорядоченное в пространстве движение - структуру. Динамическая энтропия этой структуры меньше динамической энтропии системы, существовавшей до образования структуры. Именно так происходит в недрах Солнца. Там столкновения частиц сопровождаются изменением числа частиц и излучением фотонов. В этих столкновениях суммарный импульс частиц изменяется, т.к. часть его уносят из недр Солнца фотоны и нейтрино. В результате из микроскопических неустойчивых движений частиц рождаются крупномасштабные конвективные потоки.

Работы Крылова подтвердили гипотезу Пуанкаре о динамической природе хаотичного состояния газовых систем. Хаос, который появляется в системе благодаря только внутреннему коллективному взаимодействию частиц системы, называют динамическим хаосом. Работы Крылова заложили основы теории динамического хаоса, которая стала очень популярной в последние годы не только среди физиков и математиков, но и среди экономистов и социологов. Дело в том, что в динамическом хаосе происходят процессы самоорганизации структур. Тип структуры и время ее жизни зависят от свойств коллективного взаимодействия. Коллективное взаимодействие в принципе можно контролировать, поэтому можно продлевать жизнь нужных структур и сокращать cуществование ненужных.

Структуры, рождающиеся в динамическом хаосе, не повторяются. Действительно, структура рождается из неустойчивого состояния благодаря коллективному взаимодействию. Точное повторение структуры означало бы возможность точного возврата в исходное неустойчивое состояние, но тогда это состояние не является неустойчивым.

Неповторимость структур динамического хаоса позволяет решить «проблему времени». В нашем мире существует необратимое течение времени, наблюдаемое как последовательность неповторимых событий, потому что пространство однородно и изотропно, время течет равномерно, скорость распространения взаимодействий ограничена скоростью света в вакууме и, наконец, существует коллективное взаимодействие частиц и физических полей. Это время является своеобразным математическим образом неограниченного процесса самоорганизации материи. Теперь мы можем согласиться с Платоном, который утверждал, что время превращает хаос во Вселенную.