Задачи из-за кордона

Закон сохранения импульса. Системы нескольких тел. Столкновения

50. (II) Шарик массой m сталкивается абсолютно упруго с покоящимся шариком и отскакивает от него со скоростью, равной трети исходной. Какова масса второго шарика, если удар центральный?

A ball of mass m makes a head-on-elastic collision with a second ball (at rest) and rebounds with a speed equal to one-third its original speed. What is the mass of the second ball?

Решение

Если скорость шарика массой m до столкновения равна v1, после столкновения u, скорость первоначально покоящегося шарика массой m₂ после столкновения равна v₂, то, написав законы сохранения импульса и энергии (см. решение задачи 49 в № 45/2000),
получим: 
аналогично, если  

Ответ. Масса покоящегося шарика в два раза больше (или в два раза меньше) массы налетающего.

51. (II) Брусок массой m = 1,0 кг скользит по наклонной плоскости (угол 37°, высота 3,6 м) и сталкивается с бруском массой М = 3,0 кг, лежащим на горизонтальной плоскости у основания клина. Считая столкновение центральным и упругим и пренебрегая трением, определите: а) абсолютное значение скоростей обоих брусков после столкновения; б) высоту (по вертикали), на которую поднимется меньший брусок.

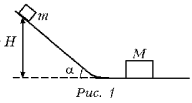
A block of mass m = 1.0 kg slides down a 37° incline 3.6 m high. At the bottom, it strikes a block of mass M = 3.0 kg at rest on a horizontal surface (see Fig. 1). If the collision is elastic and friction can be ignored, determine (a) the speeds of the two blocks after the collision and (b) to what vertical height up the incline the smaller mass will go.

[Зря за кордоном думают, что заданный наклон плоскости играет какую-то роль. Это не так. Важно другое, о чем авторы умалчивают: переход от наклонной плоскости к горизонтали должен быть гладким (на рисунке он показан тонкой линией), иначе меньший брусок будет не скользить по горизонтали, а скакать. – Ред.]

Решение

Так как удар абсолютно упругий и тела движутся по одной прямой, то снова применимы формулы решения задачи 49. Скорость меньшего бруска m после соударения равна:

Знак «–» указывает, что скорость направлена влево. Высота, на которую он поднимется после соударения, равна Скорость большего бруска после удара:

Ответ. После столкновения скорости обоих брусков по модулю одинаковы и равны 4,2 м/с, меньший брусок поднимется на высоту 0,9 м.

52. (II) Покажите, что в результате любого абсолютно упругого центрального столкновения двух тел, двигавшихся по одной прямой, их скорости будут равны:

Show that, in general, for any head-on, one-dimensional, elastic collision, the speeds after collision are:

 Решение

Запишем законы сохранения импульса и энергии:

Группируя в (1) члены с одинаковыми массами, получаем:

Разделив в (2) одно уравнение на другое, получим:

Выразив из (3) и воспользовавшись уравнением для закона сохранения импульса в (1), получим первое из требуемых соотношений, для . Подставив его в (3), получим формулу для .

53. (II) Вычислите ту часть кинетической энергии, которую теряет нейтрон (m₁ = 1,01 а.е.м.) при упругом центральном столкновении с: а)б) (дейтерий, m = 2,01 а.е.м); в) (m = 12,00 а.е.м.); г) (свинец, m = 208 а.е.м.). Что вы думаете об эффективности применения каждого из указанных веществ в ядерном реакторе в качестве замедлителя?

Determine the fraction of kinetic energy lost by a neutron (m₁ = 1.01 u) when it collides head-on and ellastically with
(a) (m = 1.01 u); (b) ( heavy hydrogen, m = 2.01 u); (c) (m = 12.00 u); (d) (lead, m = 208 u). Discuss the fulfilness of each of these as a moderator in a nuclear reactor.

Решение

Если скорость нейтрона до столкновения равна v, после столкновения равна u, то часть кинетической энергии, которую теряет нейтрон, равна

Ответ. При упругом центральном столкновении с атомом водорода нейтрон теряет всю свою энергию, в то время как при столкновении с атомом дейтерия он теряет 89%, с атомом углерода – 29%, с атомом свинца – 1,9%. [В ядерном реакторе в качестве замедлителя целесообразно применять водород или дейтерий. Реально используются вода, графит и другие вещества, содержащие легкие ядра. – Ред.]

54. (II) Найдите наибольшую массу m в задаче 51 (см. рис. 1), при которой маленький брусок, отразившись от большого бруска и поднявшись по наклонной плоскости, вновь соскользнет вниз и еще раз ударит М.

In problem 51 (Fig.1), what is the upper limit on the mass m if it is to rebound from M and return down the incline and collide with M again?

Решение

Так как механическая энергия сохраняется, после повторного спуска маленький брусок будет иметь такую же скорость, как сразу после удара, но направленную вправо. Тела вновь столкнутся, если |u| > |v₂|, – формулы для u и v2 приведены в решении задачи 51. Отсюда получается условие: m < M/3. При m = M/3 скорости тел будут равны, и второго столкновения не произойдет.

Ответ. Второе столкновение произойдет, если m < M/3.

55. (III) Брусок массой 2,0 кг скользит по гладкому столу со скоростью 8,0 м/с в направлении покоящегося бруска массой 4,5 кг. Ко второму бруску прикреплена круглая пружина жесткостью k = 850 Н/м (рис. 2). а) На какую длину сожмется пружина, когда первый

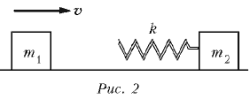
брусок столкнется со вторым? б) С какими скоростями будут двигаться бруски после этого? в) Является ли такое столкновение упругим?

A 2.0-kg block slides along a frictionless tabletop at 8.0 m/s toward a second block (at rest) of mass 4.5 kg. A coil spring, which obeys Hook,s law and has spring constant k = 850 N/m, is attached to the second block in such a way that it will be compressed when struck by the moving block (Fig. 2). (a) What will be the maximum compression of the spring? (b) What will be the final velocities of the blocks after the collision? (c) Is the collision elastic?

Решение

Будем считать пружину невесомой и решать задачу в системе отсчета, связанной с центром масс. Так как горизонтальных внешних сил нет, центр масс будет двигаться с постоянной относительно стола скоростью . В системе центра масс до столкновения тела движутся навстречу друг другу со скоростями v₁ = v₀ –V_цм = 5,54 м/с и v₂ = –V_цм соответственно. В момент наибольшего сжатия пружины скорости тел станут равными нулю. При этом вся кинетическая энергия движения перейдет в потенциальную энергию упругости пружины:

.Отсюда вычисляем максимальное сжатие пружины x = 32 см. После столкновения бруски будут двигаться в системе центра масс в противоположных направлениях с такими же скоростями, как и до него. Такое столкновение является упругим. Относительно стола первый брусок будет двигаться влево со скоростью v₁ – V_цм = 3,08 м/с, а второй – вправо со скоростью 2V_цм = 4,92 м/с.

Ответ. Пружина сожмется на 32 см; после столкновения скорости в системе центра масс по величине не изменятся; столкновение является упругим. Относительно стола после столкновения первый брусок имеет скорость 3,08 м/с, второй – 4,92 м/с.

Другой вариант решения.

Запишем законы сохранения энергии и импульса до столкновения и в момент наибольшего сжатия пружины, когда оба бруска скользят с одинаковой скоростью V, а часть кинетической энергии перешла в потенциальную энергию сжатия. Тогда:

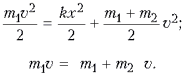
 Выражая v из второго уравнения и подставляя в первое, получаем:

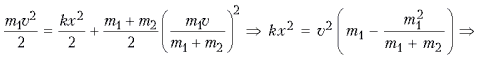
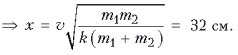
После столкновения пружина разожмется, потенциальная энергия сжатия станет вновь равна нулю (перейдет в кинетическую энергию движения брусков). Такое столкновение является упругим.

Применяя решения задачи 49 для скорости первого бруска, имеем:

Для второго бруска:

*56. (II) Пользуясь законом сохранения импульса (в векторной форме), покажите, что столкновение любых двух тел происходит в одной плоскости, если: а) одно из этих тел покоится; б) исходные скорости обеих частиц направлены по одной прямой.

Use conservation of (vector) momentum to show that a two-particle collision occurs in a plane if: (a) one particle is initially at rest; (b) the two particles have initial velocities in the same or opposite directions.

Решение

При выполнении условий а и б все векторы скоростей лежат в одной плоскости.
По закону сохранения импульса: а) m₁v₁ = m₁u₁ + m₂u₂; б) m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂. Если три вектора линейно зависимы, то они лежат в одной плоскости. Это свойство пространства.