XXXIV всероссийская
олимпиада школьников
Пермь-2000
9–11-й классы
Теоретический тур 9-й
класс
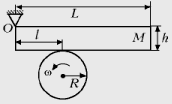 Задача 1. К диску радиусом R,
насаженному на горизонтальный вал мотора, под
действием силы тяжести прижимается тяжелый
брусок массой M. Брусок может свободно
поворачиваться относительно оси O. Длина
бруска равна L, толщина h. Точка
соприкосновения бруска с диском находится на
расстоянии l от левого края бруска.
Коэффициент трения скольжения между бруском и
диском равен m. Предполагая, что мотор может развивать
мощность P, определите угловую скорость w
вращения диска в зависимости от величины l.
Рассмотрите случаи вращения диска по (w+) и
против (w–)
часовой стрелки. Постройте качественные графики w+(l) и w–(l).
Задача 1. К диску радиусом R,
насаженному на горизонтальный вал мотора, под
действием силы тяжести прижимается тяжелый
брусок массой M. Брусок может свободно
поворачиваться относительно оси O. Длина
бруска равна L, толщина h. Точка
соприкосновения бруска с диском находится на
расстоянии l от левого края бруска.
Коэффициент трения скольжения между бруском и
диском равен m. Предполагая, что мотор может развивать
мощность P, определите угловую скорость w
вращения диска в зависимости от величины l.
Рассмотрите случаи вращения диска по (w+) и
против (w–)
часовой стрелки. Постройте качественные графики w+(l) и w–(l).
Решение
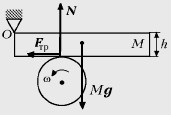 Рассмотрим случай
вращения диска против часовой стрелки. Условие
равновесия бруска:
Рассмотрим случай
вращения диска против часовой стрелки. Условие
равновесия бруска:
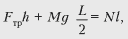
где Fтр = mN. Отсюда 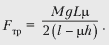
При установившейся скорости
вращения P = FтрRw–.
Следовательно,
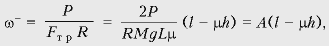
 где
где 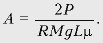 Решение
задачи существует при l > mh.
Решение
задачи существует при l > mh.
При l Ј mh происходит
«заклинивание»: мотор не может провернуть диск.
Для вращения по часовой
стрелке можно получить w+ = A(l + mh) –
«заклинивания» нет.
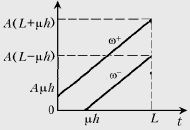
Графики w+(l) и w–(l) имеют вид,
представленный на рисунке.
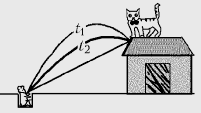 Задача 2. Кот Леопольд стоял у
края крыши сарая. Два злобных мышонка выстрелили
в него из рогатки. Однако камень, описав дугу,
через t1 = 1,2 с упруго отразился
от наклонного ската крыши сарая у самых лап кота
и через t2 = 1,0 с попал в лапу
стрелявшего мышонка. На каком расстоянии s от
мышат находился кот Леопольд?
Задача 2. Кот Леопольд стоял у
края крыши сарая. Два злобных мышонка выстрелили
в него из рогатки. Однако камень, описав дугу,
через t1 = 1,2 с упруго отразился
от наклонного ската крыши сарая у самых лап кота
и через t2 = 1,0 с попал в лапу
стрелявшего мышонка. На каком расстоянии s от
мышат находился кот Леопольд?
Решение
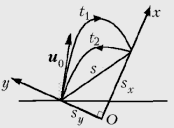 Пусть u0 –
вектор начальной скорости камня, uк –
вектор скорости камня в момент его попадания в
лапу мышонка. Направим ось Ox вдоль ската крыши,
ось Oy – перпендикулярно ей через лапу мышонка.
Пусть u0 –
вектор начальной скорости камня, uк –
вектор скорости камня в момент его попадания в
лапу мышонка. Направим ось Ox вдоль ската крыши,
ось Oy – перпендикулярно ей через лапу мышонка.
Из закона сохранения энергии
следует:|u0| = |uк|.
(1)
Проекция вектора скорости
камня на ось Ox непосредственно перед ударом о
скат крыши равна проекции скорости на эту же ось
сразу после удара. Тогда |u0x| = |uкx|.
(2)
Из (1) и (2) следует, что |u0y| = |uкy|.
В проекциях на оси Ox и Oy можно записать
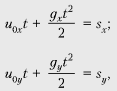 |
(3)
(4)
|
где gx и gy –
проекции g на соответствующие оси. По
теореме Виета, уравнения (3) и (4) можно
преобразовать к виду:
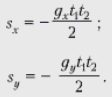 |
(5)
(6)
|
Тогда 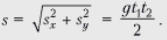
Задача 3. Известно, что
дистиллированную воду, очищенную от примесей,
можно охладить без превращения в лед ниже
температуры t0 = 0 °С. В
зависимости от внешнего давления процесс
кристаллизации воды может начаться при
некоторой температуре t1 < t0.
Образовавшийся при этом лед отличается по своим
физическим свойствам от обычного льда при
температуре 0 °С. Определите, чему равна
удельная теплота плавления льда (l2) при
температуре t1 = –10 °С. Удельную
теплоемкость воды в интервале температур от – 10
до 0 °С примите равной c1 = 4,17 • 103 Дж/(кг • К).
Удельную теплоемкость льда в этом интервале
температур примите равной c2 = 2,17 • 103 Дж/(кг •
К). Удельная теплота плавления льда при
температуре 0 °С равна l1 = 3,32 • 105 Дж/кг.
Решение
Решение задачи поясняет
схема, приведенная ниже.
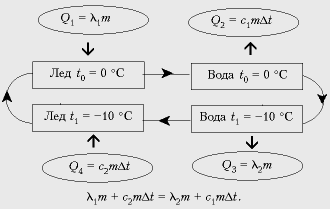
Отсюда следует: 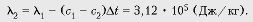
 Задача 4. Дан «черный ящик» с
тремя выводами. Известно, что внутри ящика
находится некоторая схема, составленная из
резисторов. Если к выводам 1, 3 подключить
источник напряжения U = 15 В и измерить с
помощью вольтметра напряжения между выводами 1,
2 и 2, 3, то они оказываются равными U12 = 6 В
и U23 = 9 В. Если источ-
Задача 4. Дан «черный ящик» с
тремя выводами. Известно, что внутри ящика
находится некоторая схема, составленная из
резисторов. Если к выводам 1, 3 подключить
источник напряжения U = 15 В и измерить с
помощью вольтметра напряжения между выводами 1,
2 и 2, 3, то они оказываются равными U12 = 6 В
и U23 = 9 В. Если источ-
ник напряжения подключить к
выводам 2, 3, то U21 = 10 В,
U13 = 5 В. Какими будут напряжения U13,
U32, если источник подключить к выводам 1, 2?
Нарисуйте возможные схемы «черного ящика» с
минимальным числом резисторов. Полагая, что
наименьшее сопротивление из всех резисторов
равно R, найдите сопротивления остальных
резисторов.
Решение
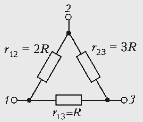 Рассмотрим
соединение «треугольником». Тогда при
подключении источника питания к клеммам 1, 3 по
ветви 1–2–3 будет течь ток I, поэтому U12 = Ir12,
а U23 = Ir23. Отсюда
Рассмотрим
соединение «треугольником». Тогда при
подключении источника питания к клеммам 1, 3 по
ветви 1–2–3 будет течь ток I, поэтому U12 = Ir12,
а U23 = Ir23. Отсюда 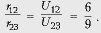 Аналогично, для случая подключения
источника питания к выходам 2, 3 можно записать
Аналогично, для случая подключения
источника питания к выходам 2, 3 можно записать
r12/r13 = U21/U13= 10/5. Тогда
получим r13 < r12 < r23.
Значит, r13 = R, r12 = 2R, а r23 = 3R.
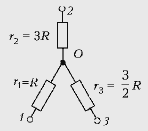 При соединении «звездой» получаем,
что при подключении источника питания к клеммам 1
и 3 ток I13 идет только по ветви 1–0–3,
поэтому U12 = I13r1,
U23 = I13r3, а при
подключении к клеммам 2, 3 U21 = I23r2
и U13 = I23r3.
Отсюда r1 < r3 < r2,
значит,
При соединении «звездой» получаем,
что при подключении источника питания к клеммам 1
и 3 ток I13 идет только по ветви 1–0–3,
поэтому U12 = I13r1,
U23 = I13r3, а при
подключении к клеммам 2, 3 U21 = I23r2
и U13 = I23r3.
Отсюда r1 < r3 < r2,
значит, 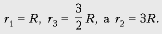
Эти две схемы полностью
эквивалентны, поэтому напряжения U13 и U23
можно вычислять по любой из них. Воспользуемся
«звездой»:
U13 = Ir1;
U23 = Ir2; U13 + U23 = U.
Отсюда получаем: U23/U13
= 3/1 и U13 = U/4 = = 15В/4 = 3,75 В,
U23 = 45В/4 = 11,25 В.

 Задача 1. К диску радиусом R,
насаженному на горизонтальный вал мотора, под
действием силы тяжести прижимается тяжелый
брусок массой M. Брусок может свободно
поворачиваться относительно оси O. Длина
бруска равна L, толщина h. Точка
соприкосновения бруска с диском находится на
расстоянии l от левого края бруска.
Коэффициент трения скольжения между бруском и
диском равен m. Предполагая, что мотор может развивать
мощность P, определите угловую скорость w
вращения диска в зависимости от величины l.
Рассмотрите случаи вращения диска по (w+) и
против (w–)
часовой стрелки. Постройте качественные графики w+(l) и w–(l).
Задача 1. К диску радиусом R,
насаженному на горизонтальный вал мотора, под
действием силы тяжести прижимается тяжелый
брусок массой M. Брусок может свободно
поворачиваться относительно оси O. Длина
бруска равна L, толщина h. Точка
соприкосновения бруска с диском находится на
расстоянии l от левого края бруска.
Коэффициент трения скольжения между бруском и
диском равен m. Предполагая, что мотор может развивать
мощность P, определите угловую скорость w
вращения диска в зависимости от величины l.
Рассмотрите случаи вращения диска по (w+) и
против (w–)
часовой стрелки. Постройте качественные графики w+(l) и w–(l). Рассмотрим случай
вращения диска против часовой стрелки. Условие
равновесия бруска:
Рассмотрим случай
вращения диска против часовой стрелки. Условие
равновесия бруска: где
где  Задача 2. Кот Леопольд стоял у
края крыши сарая. Два злобных мышонка выстрелили
в него из рогатки. Однако камень, описав дугу,
через t1 = 1,2 с упруго отразился
от наклонного ската крыши сарая у самых лап кота
и через t2 = 1,0 с попал в лапу
стрелявшего мышонка. На каком расстоянии s от
мышат находился кот Леопольд?
Задача 2. Кот Леопольд стоял у
края крыши сарая. Два злобных мышонка выстрелили
в него из рогатки. Однако камень, описав дугу,
через t1 = 1,2 с упруго отразился
от наклонного ската крыши сарая у самых лап кота
и через t2 = 1,0 с попал в лапу
стрелявшего мышонка. На каком расстоянии s от
мышат находился кот Леопольд? Пусть u0 –
вектор начальной скорости камня, uк –
вектор скорости камня в момент его попадания в
лапу мышонка. Направим ось Ox вдоль ската крыши,
ось Oy – перпендикулярно ей через лапу мышонка.
Пусть u0 –
вектор начальной скорости камня, uк –
вектор скорости камня в момент его попадания в
лапу мышонка. Направим ось Ox вдоль ската крыши,
ось Oy – перпендикулярно ей через лапу мышонка. 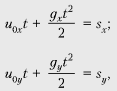
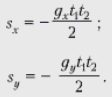

 Рассмотрим
соединение «треугольником». Тогда при
подключении источника питания к клеммам 1, 3 по
ветви 1–2–3 будет течь ток I, поэтому U12 = Ir12,
а U23 = Ir23. Отсюда
Рассмотрим
соединение «треугольником». Тогда при
подключении источника питания к клеммам 1, 3 по
ветви 1–2–3 будет течь ток I, поэтому U12 = Ir12,
а U23 = Ir23. Отсюда 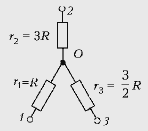 При соединении «звездой» получаем,
что при подключении источника питания к клеммам 1
и 3 ток I13 идет только по ветви 1–0–3,
поэтому U12 = I13r1,
U23 = I13r3, а при
подключении к клеммам 2, 3 U21 = I23r2
и U13 = I23r3.
Отсюда r1 < r3 < r2,
значит,
При соединении «звездой» получаем,
что при подключении источника питания к клеммам 1
и 3 ток I13 идет только по ветви 1–0–3,
поэтому U12 = I13r1,
U23 = I13r3, а при
подключении к клеммам 2, 3 U21 = I23r2
и U13 = I23r3.
Отсюда r1 < r3 < r2,
значит,