1. При нагревании газа получена
зависимость, показанная на рисунке. Определите,
сжимался газ или расширялся? [Масса газа
постоянна. – Ред.]10-й класс. углубленный курс
Метод решения задач с использованием диаграмм состояния успешно зарекомендовал себя при изуче- нии тем «Газовые законы», «Термодинамика», «Тепловые двигатели». Этот метод может быть использован также и на уроках, и на факультативных занятиях.
1. При нагревании газа получена
зависимость, показанная на рисунке. Определите,
сжимался газ или расширялся? [Масса газа
постоянна. – Ред.]
Решение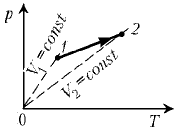
Нужно провести из начала координат прямые (пунктир на чертеже),
проходящие через состояния 1 и 2.
Эти прямые соответствуют процессам при постоянных объемах V1 и V2.
Поскольку V2 > V1, газ расширялся.
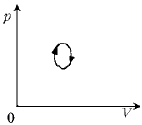
2. Как менялась температура [заданной массы. – Ред.] идеального газа (увеличивалась или уменьшалась) в процессе, график которого в координатах p, V изображен на рисунке?
Решение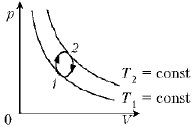
Проведем гиперболы, касательные к кривой. Так как гипербола в координатах p, V является графиком изотермы: pV = nRT = const, то T1 < T2. Следовательно, от состояния 1 до состояния 2 температура газа повышалась, а от состояния 2 до состояния 1 – понижалась.
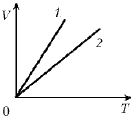
3. Получены две экспериментальные зависимости (см. рисунок). В каком случае масса газа больше? Давление в первом и во втором случае одинаково.
Решение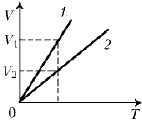
Так как V1 > V2, то m1 > m2.
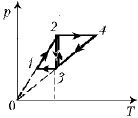4. Над идеальным газом производят
два замкнутых процесса: 1–2–3–1 и 3–2–4–3.
В каком из них газ совершает бо1льшую работу?
Решение
Изобразим изменение состояния газа на p–V-диаграмме.
Очевидно, что А2 > А1.
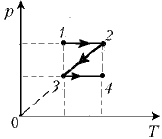5. Моль идеального одноатомного
газа переводится из начального состояния 1 в
конечное состояние 4 в ходе процесса 1–2–3–4.
определите подведенное к газу количество
теплоты, если разность начальной и конечной
температур DT = 100 К. Считать R = 8,3 Дж/(моль • К).
Решение
|
|
Из р–Т-диаграммы видно, что T2 – T1 = T4 – T3 = DТ.
Воспользуемся формулой Q = DU + A ':
– тепло подводится;
– тепло отводится, T уменьшается;
– тепло подводится.
6. Моль одноатомного [идеального.
– Ред.] газа совершает замкнутый цикл,
состоящий из трех процессов: адиабатического
расширения, изотермического сжатия и изохорного
нагревания. Какая работа была совершена газом в
адиабатическом процессе, если при изохорном
нагревании подвели Q = 10 кДж тепла? R = 8,3 Дж/(К • моль).
[Для произвольного идеального газа результат тот
же. – Ред.]
Решение
Q12 = 0 Ю = –DU12 .
T2 = T3 Ю – DU31 = DU12.
V1 = V3 Ю Q31 = DU31 = 10 кДж, т.к. A'31 = 0.
Таким образом, A '12 = –DU12 = DU31 = Q31 = 10 кДж.
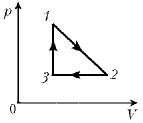7. Один моль одноатомного
идеального газа совершает замкнутый цикл,
состоящий из процесса с линейной зависимостью
давления от объема, изобары и изохоры. Найдите
количество теплоты, подведенное к газу на
участках цикла, где его температура растет.
Температура газа в состояниях 1 и 2 равна
300 К. Отношение объемов на изобаре 
Направление обхода цикла
указано стрелками. R = 8,3 Дж/(моль • К).
Решение
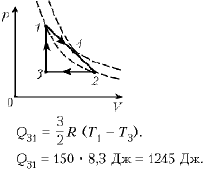
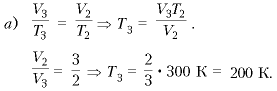
б) На участке 1–2 p = a – bV, т.е.:
p1 = a – bV1;
p2 = a – bV2.
Решая систему, находим:
Таким образом, 
Умножив обе части на V, получим:
На участке 1–4 температура растет!
в)
Qподвед = Q31 + Q14 = 1245 Дж + 726,25 Дж d 1970 Дж.
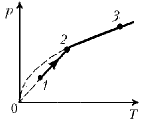8. Состояние [одного моля
идеального одноатомного. – Ред.] газа
меняется, как представлено на диаграмме p, T,
причем p ~ T на участке 1–2 и 
на участке 2–3. Найдите теплоемкости газа
на участках 1–2 и 2–3.
Решение
а) На участке 1–2 
б) На участке 2–3 
таким
образом, V ~ p. Работа газа в этом
случае:
[В решении этой задачи помещен рисунок, предложенный редакцией, т.к. авторский рисунок ошибочен. – Ред]
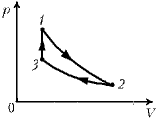
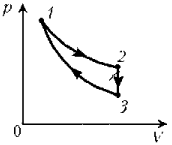9. КПД тепловой машины,
работающей по циклу, состоящему из изотермы 1–2,
изохоры 2–3 и адиабаты 3–1, равен h. Разность
максимальной и минимальной температур газа в
цикле равна DT.
Найдите работу, совершенную n молями одноатомного идеального газа в изотермическом процессе.
Решение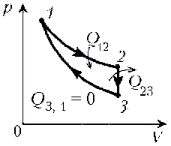
Q12 – количество теплоты, полученное от нагревателя; Q23 – количество теплоты, отданное холодильнику; Q31 = 0, т.к. 3–1 – адиабата.
Итак:
(адиабата);
(изотерма).
Поэтому
Задачи для самостоятельного решения
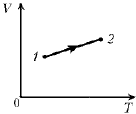1. Поршень в цилиндре с воздухом
прилегает к стенкам цилиндра неплотно, поэтому
медленно пропускает воздух. Снятая во время
нагревания при постоянном давлении зависимость
объема от температуры изображена на рисунке.
Увеличивалась или уменьшалась масса воздуха в
цилиндре? (Ответ. Масса газа в состоянии 1
больше, чем в состоянии 2.)
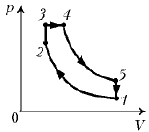
2. На рисунке показан циклический процесс, проведенный над некоторой массой [идеального. – Ред.] газа. Изобразите этот процесс в координатах p, T и V, T (1–2 и 4–5 – изотермы).
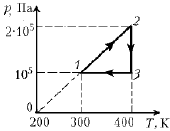3. На p–T-диаграмме изображен
замкнутый процесс, который совершает некоторая
масса кислорода. Известно, что максимальный
объем, который занимал газ в этом процессе, Vмакс = 16,6 дм3.
Определите массу газа и его объем в точке 1.
Значения T1, T2, p1 и p2
указаны на рисунке.
(Ответ. V1 = 12,4 дм3; m = 16 г.)
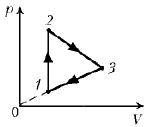
4. Найдите работу,
совершаемую молем идеального газа в цикле,
состоящем из двух участков линейной зависимости
давления от объема и изохоры. Точки 1 и 3
лежат на прямой, проходящей через начало
координат. Температуры в точках 2 и 3
одинаковы. Считать заданными температуры T1
и T2 в точках 1 и 2. (Ответ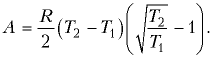 
)
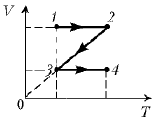
5. В тепловом процессе моль [одноатомного. – Ред.] идеального газа переводят из начального состояния в конечное, как показано на рисунке. Какое количество теплоты подведено к газу, если разность начальной и конечной температур DT = 100 °C? (Ответ. 415 Дж.)
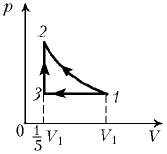
6. Моль идеального газа переводят из состояния 1 в состояние 2: в первом случае – адиабатически, а во втором – сначала по изобаре 1–3, а затем по изохоре 3–2.
Минимальная температура Tмин = 300 К. Количество теплоты, подведенное к газу в процессе 1–3–2, равно 2,6 кДж. Чему равна работа газа в адиабатическом процессе?
(Ответ. А12 = – 12 560 Дж.)
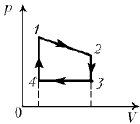
7. Один моль идеального газа изменяет свое состояние согласно представленному циклу. 1–4 и 2–3 – изохоры, 3–4 – изобара, 1–2 – прямая. Температуры в состояниях 1, 2, 3, 4 равны соответственно T1, T2, T3, T4. Какую работу совершает газ за один цикл?
(Ответ. 
.)
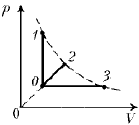
8. В каждом из процессов, изображенных на диаграмме, температура изменяется на одну и ту же величину. В каком из этих процессов газ получает наибольшее количество теплоты? (Ответ. в изобарном процессе.)
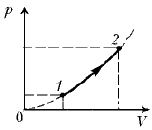9. Состояние [моля идеального. – Ред.]
газа меняется, как представлено на диаграмме p, V,
причем p ~ V2 на участке 1–2.
Найдите теплоемкость газа в этом процессе. (Ответ. 
.)
[Авторский ответ 
ошибочен.
– Ред.]
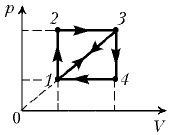
4 10. Найдите КПД тепловых машин, работающих по циклам 1–2–3–1 и 1–3–4–1, если КПД машины, работающей по циклу 1–2–3–4–1, равен h. В качестве рабочего тела во всех слу-
чаях используется [один и тот же. – Ред.] идеальный газ.
(Ответ: 
)
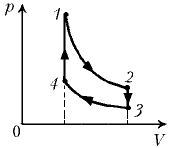
44 11. Определите КПД цикла, состоящего из двух адиабат и двух изохор, совершаемого одноатомным идеальным газом. Известно, что в процессе адиабатного расширения устанавливается температура T2 = 0,75 T1, а в
процессе адиабатного сжатия T3 = 0,75 T4. (Ответ: h = 25 %.)
[Для произвольного идеального газа результат тот же. – Ред.]
