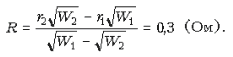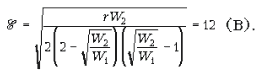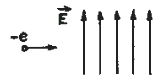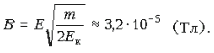С.С.Чесноков, Г.Я.Мякишев,
С.Ю.Никитин,
Н.Б.Подымова, М.С.Полякова, В.И.Шмальгаузен,
физический факультет МГУ, г. Москва
Хочу учиться на
ВМК!
Задачи,
предлагавшиеся на устных вступительных
экзаменах
на факультет вычислительной математики и
кибернетики МГУ им. М.В.Ломоносова в 1999 г.
III. ЭЛЕКТРОДИНАМИКА
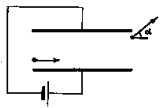 1 Заряженная частица влетает в
пространство между пластинами плоского
конденсатора, напряжение на котором
поддерживается постоянным. Начальная скорость
частицы параллельна пластинам конденсатора. При
вылете из конденсатора скорость частицы
составила угол a = 60° с ее начальной скоростью. Под
каким углом b к начальной скорости вылетит эта
частица из конденсатора, если расстояние между
его пластинами увеличить в k = 3 раза? Силу
тяжести не учитывать.
1 Заряженная частица влетает в
пространство между пластинами плоского
конденсатора, напряжение на котором
поддерживается постоянным. Начальная скорость
частицы параллельна пластинам конденсатора. При
вылете из конденсатора скорость частицы
составила угол a = 60° с ее начальной скоростью. Под
каким углом b к начальной скорости вылетит эта
частица из конденсатора, если расстояние между
его пластинами увеличить в k = 3 раза? Силу
тяжести не учитывать.
Решение
Определим вначале, как
зависит угол вылета частицы из конденсатора от
ее заряда q, массы m и начальной скорости v0,
а также от параметров электрической системы.
Обозначим через U напряжение на зажимах
источника, L – длину пластин, d0 –
начальное расстояние между ними. В пространстве
между пластинами на частицу действует сила F
= qE, направленная вдоль линий напряженности
электрического поля E в конденсаторе. В
результате движение частицы в направлении,
параллельном пластинам, будет равномерным со
скоростью v0, а в направлении,
перпендикулярном пластинам, – равноускоренным с
ускорением 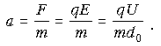
За время 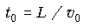 пролета частицей конденсатора
перпендикулярная пластинам составляющая
скорости частицы приобретет значение:
пролета частицей конденсатора
перпендикулярная пластинам составляющая
скорости частицы приобретет значение: 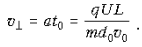
Следовательно, угол a между
начальной скоростью частицы и ее скоростью при
вылете из конденсатора определится из
соотношения: 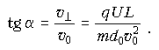
При увеличении расстояния
между пластинами в k раз угол вылета частицы
из конденсатора выразится формулой: 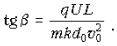
Сравнивая два последние
соотношения, получаем ответ: 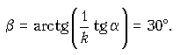
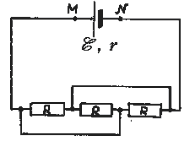
2 Батарея с ЭДС 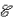 = 2 В и внутренним сопротивлением r
= 0,1 Ом присоединена к цепи, изображенной на
рисунке. Сопротивление каждого из резисторов R =
1 Ом. Найдите напряжение на клеммах батареи.
Сопротивлением всех соединительных проводов
пренебречь.
= 2 В и внутренним сопротивлением r
= 0,1 Ом присоединена к цепи, изображенной на
рисунке. Сопротивление каждого из резисторов R =
1 Ом. Найдите напряжение на клеммах батареи.
Сопротивлением всех соединительных проводов
пренебречь.
Решение
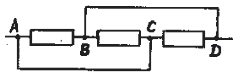
Для того чтобы определить
напряжение на клеммах батареи, необходимо
вычислить сопротивление нагрузки. Нетрудно
заметить, что потенциалы точек А и С, а
также точек В и D попарно равны.
Следовательно, все три резистора нагрузки
фактически соединены параллельно. Поэтому
сопротивление внешней цепи Rвнеш= R/3,
сила тока в цепи 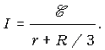 Отсюда
получаем ответ:
Отсюда
получаем ответ: 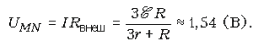
3 Во внешней нагрузке,
подключенной к батарее, выделяется мощность W1
= 1 Вт. Чему равен коэффициент полезного действия h этой цепи (т.е.
отношение мощности, выделяющейся в нагрузке, к
полной мощности, развиваемой батареей), если при
подключении той же нагрузки к двум таким
батареям, соединенным последовательно, мощность
в нагрузке стала равной W2 = 1,44 Вт?
Решение
В цепи, состоящей из батареи и
внешней нагрузки сопротивлением R, мощность,
выделяющаяся в нагрузке, равна: 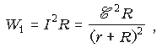
где I – ток в цепи, 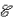 – ЭДС батареи, r – ее
внутреннее сопротивление. При этом полная
мощность, развиваемая батареей:
– ЭДС батареи, r – ее
внутреннее сопротивление. При этом полная
мощность, развиваемая батареей: 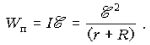
Отсюда следует, что
коэффициент полезного действия цепи: 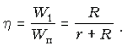
Если подключить эту же
нагрузку к двум одинаковым батареям, соединенным
последовательно, ЭДС и внутреннее сопротивление
в цепи станут равными соответственно
2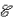 и 2r. Следовательно, мощность,
выделяющаяся в нагрузке в этом случае, будет
равна:
и 2r. Следовательно, мощность,
выделяющаяся в нагрузке в этом случае, будет
равна: 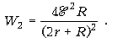
. Составим отношение: 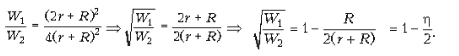
Отсюда получаем ответ: 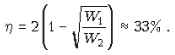
4 При подключении нагрузки к
батарее с внутренним сопротивлением r1 =
0,1 Ом во внешней цепи выделяется мощность W1
= 1 Вт. В той же нагрузке, питаемой от батареи
внутренним сопротивлением r2 = 0,2 Ом и c
равной ЭДС, выделяется мощность W2 = 0,64
Вт. Чему равно сопротивление нагрузки R?
Решение
Мощность, выделяющаяся в
нагрузке сопротивлением R, подключенной к
батарее с ЭДС 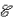 и внутренним
сопротивлением r1, равна
и внутренним
сопротивлением r1, равна 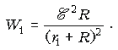 При подключении этой нагрузки к
батарее с той же ЭДС, но внутренним
сопротивлением r2, в ней будет
выделяться мощность
При подключении этой нагрузки к
батарее с той же ЭДС, но внутренним
сопротивлением r2, в ней будет
выделяться мощность 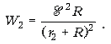 Составим отношение:
Составим отношение: 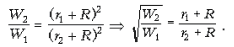
Выражая из последнего
соотношения R, получаем ответ: 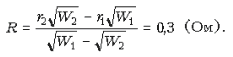
5 При подключении к
аккумулятору внутренним сопротивлением r = 0,16 Ом
нагревательный элемент потребляет мощность W1
= 200 Вт. При подключении этого же нагревательного
элемента к двум таким аккумуляторам, соединенным
последовательно, выделяемая в нем мощность
составляет W2 = 288 Вт. Найдите ЭДС 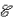 аккумулятора.
аккумулятора.
Решение
Мощность, выделяемая в
нагревательном элементе при подключении его к
одному аккумулятору, равна 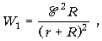 где R – сопротивление нагревателя. При
подключении этого же элемента к двум одинаковым
аккумуляторам, соединенным последовательно,
значения ЭДС и внутреннего сопротивления
удваиваются, и в нагревателе выделяется
мощность:
где R – сопротивление нагревателя. При
подключении этого же элемента к двум одинаковым
аккумуляторам, соединенным последовательно,
значения ЭДС и внутреннего сопротивления
удваиваются, и в нагревателе выделяется
мощность: 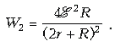
Вводя величину 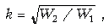 получим
получим 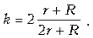 Отсюда
Отсюда 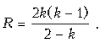
Учитывая, что 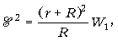 после несложных преобразований
получаем ответ:
после несложных преобразований
получаем ответ: 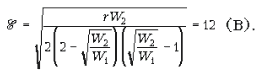
6 Электрон влетает в
однородное электрическое поле напряженностью E
= 6 ·104 В/м перпендикулярно силовым линиям.
Определите величину и направление вектора
индукции магнитного поля B, которое надо
создать в этой области пространства для того,
чтобы электрон пролетел ее, не отклоняясь от
первоначального направления. Кинетическая
энергия электрона EK=1,6•10-16 Дж,
масса электрона m = 9 · 10–31 кг. Силой
тяжести пренебречь.
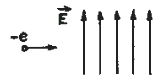
Решение
В данном однородном
электрическом поле напряженностью E
электрон движется под действием кулоновской
силы FК по параболической
траектории (здесь |e| – абсолютная величина
заряда электрона).
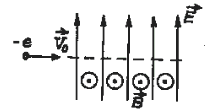
Для того чтобы электрон
двигался прямолинейно, нужно создать такое
однородное магнитное поле, в котором действующая
на электрон сила Лоренца FЛ в каждой
точке его траектории была бы равна кулоновской
силе по величине и противоположна ей по
направлению, т.е. FЛ = –FК.
Величина силы Лоренца 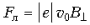 (здесь v0 – скорость электрона,
(здесь v0 – скорость электрона,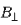 – величина составляющей вектора
магнитной индукции, перпендикулярной скорости),
ее направление определяется правилом левой руки.
Очевидно, что сила Лоренца направлена против
кулоновской силы в том случае, если магнитная
индукция направлена перпендикулярно начальной
скорости электрона и напряженности
электрического поля. Применяя правило левой
руки, с учетом того, что заряд электрона
отрицателен, находим, что вектор магнитной
индукции должен быть перпендикулярным плоскости
рисунка и направлен на нас. Составляя равенство
|e| E=|e| v0E и учитывая, что
– величина составляющей вектора
магнитной индукции, перпендикулярной скорости),
ее направление определяется правилом левой руки.
Очевидно, что сила Лоренца направлена против
кулоновской силы в том случае, если магнитная
индукция направлена перпендикулярно начальной
скорости электрона и напряженности
электрического поля. Применяя правило левой
руки, с учетом того, что заряд электрона
отрицателен, находим, что вектор магнитной
индукции должен быть перпендикулярным плоскости
рисунка и направлен на нас. Составляя равенство
|e| E=|e| v0E и учитывая, что 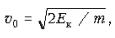 получаем ответ:
получаем ответ: 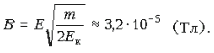

 1 Заряженная частица влетает в
пространство между пластинами плоского
конденсатора, напряжение на котором
поддерживается постоянным. Начальная скорость
частицы параллельна пластинам конденсатора. При
вылете из конденсатора скорость частицы
составила угол a = 60° с ее начальной скоростью. Под
каким углом b к начальной скорости вылетит эта
частица из конденсатора, если расстояние между
его пластинами увеличить в k = 3 раза? Силу
тяжести не учитывать.
1 Заряженная частица влетает в
пространство между пластинами плоского
конденсатора, напряжение на котором
поддерживается постоянным. Начальная скорость
частицы параллельна пластинам конденсатора. При
вылете из конденсатора скорость частицы
составила угол a = 60° с ее начальной скоростью. Под
каким углом b к начальной скорости вылетит эта
частица из конденсатора, если расстояние между
его пластинами увеличить в k = 3 раза? Силу
тяжести не учитывать.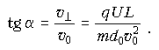
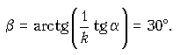


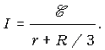 Отсюда
получаем ответ:
Отсюда
получаем ответ: 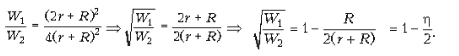
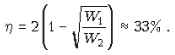
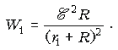 При подключении этой нагрузки к
батарее с той же ЭДС, но внутренним
сопротивлением r2, в ней будет
выделяться мощность
При подключении этой нагрузки к
батарее с той же ЭДС, но внутренним
сопротивлением r2, в ней будет
выделяться мощность