АБИТУРИЕНТУ |
С.С.Чесноков,
Г.Я.Мякишев, С.Ю.Никитин,
Н.Б.Подымова, М.С.Полякова, В.И.Шмальгаузен,
физический факультет МГУ, г. Москва
МЕХАНИКА
1
В кабине лифта высотой Н = 2,5 м, движущейся с ускорением а = 0,8 м/с2, направленным вниз, с высоты h = 0,5 м от пола вертикально вверх бросают маленький шарик. С какой начальной скоростью v0 относительно лифта брошен шарик, если после броска он поднялся точно до потолка кабины?
Решение
Используем неподвижную систему координат, начало которой совместим с полом кабины лифта в момент броска шарика, а ось Oy направим вертикально вверх. Обозначим через yш и v координату шарика и его скорость, через yк и u – координату потолка кабины и скорость кабины. Пусть скорость кабины в момент броска равна u0 и направлена вверх (ниже мы убедимся в том, что ни от величины, ни от направления скорости кабины в момент броска ответ не зависит, но для ясности рассуждений введем на данном этапе решения эту скорость). Для координат и скоростей шарика и потолка кабины справедливы кинематические уравнения:
Первые два записаны при стандартном предположении о том, что сопротивлением воздуха при движении шарика можно пренебречь. Начало отсчета времени совпадает с моментом броска шарика.
Согласно условию задачи шарик после броска поднимается точно до потолка кабины. Обозначив этот момент времени через t0, можно записать следующие соотношения:
Второе соотношение дает:
Подставляя найденное t0 в первое соотношение, после несложных преобразований находим:
2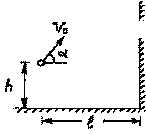
Мальчик бросает мяч в направлении вертикальной стены так, чтобы мяч, отскочив от стены, упал точно к его ногам. Какова должна быть начальная скорость мяча v0, если бросок производится с высоты h = 1,5 м под углом a к горизонту? Расстояние от мальчика до стены l = 6 м. Удар мяча о стену считать абсолютно упругим, ускорение свободного падения g = 10 м/с2.
Решение
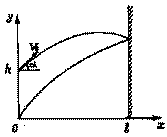
Используем стандартное предположение о том, что сопротивление воздуха при движении мяча можно не учитывать. Для того чтобы мяч, отскочив от стены, упал точно к ногам мальчика, траектория мяча должна иметь вид, изображенный на рисунке.
При упругом ударе о неподвижную
стенку нормальная к стенке составляющая
скорости мяча меняет направление на
противоположное, оставаясь такой же по величине. касательная к стенке составляющая скорости мяча не меняется. В результате угол между нормалью к стенке и скоростью мяча перед ударом оказывается равным по величине углу между нормалью к стенке и скоростью мяча после удара.
Обозначим через t0 время полета мяча. За это время он проходит по горизонтали путь 2l. Учитывая, что горизонтальная составляющая скорости мяча равна и при полете не меняется по величине, можно записать равенство:
откуда время полета мяча:
С другой стороны, по условию задачи, в момент времени t0, вертикальная координата мяча должна обратиться в нуль, т.е.:
Подставляя сюда найденное t0, после несложных преобразований находим ответ:
3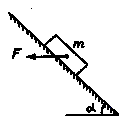
Брусок массой m = 1 кг находится на неподвижной наклонной плоскости, составляющей угол a = 45° с горизонтом. С какой минимальной горизонтальной силой F нужно действовать на брусок, чтобы он покоился? Коэффициент трения бруска о наклонную плоскость m = 0,25, ускорение свободного падения g = 10 м/с2.
Решение
Брусок находится в покое
(равновесии), если векторная сумма действующих на
него сил равна нулю. Согласно закону сухого
трения проекция силы трения покоя Fтр
может принимать любые значения из диапазона 
, где N – сила нормального давления бруска на
плоскость. Сила F минимальна, если сила трения
покоя, действующая на брусок, направлена вдоль
наклонной плоскости вверх и достигает
максимальной величины 
Записывая
уравнение равновесия бруска в проекциях на
выбранные координатные оси, получаем:
Разрешая эту систему относительно F, находим ответ:
Заметим, что при превышении силой F найденного минимального значения сила трения покоя будет уменьшаться по величине, при некотором значении силы F обратится в нуль, затем поменяет направление на противоположное. Это соответствует изменению знака Fтр в системе уравнений, описывающих равновесие бруска. Вплоть до достижения силой трения покоя значения брусок будет оставаться в покое. Проводя аналогичные рассуждения, легко получить максимальное значение силы F, при котором движение бруска вверх по наклонной плоскости еще не начнется. Следовательно, условия равновесия бруска выполняются для всех значений силы из диапазона .
4
Два тела массами m1 = 0,4 кг и m2 = 0,1 кг соединены невесомой и нерастяжимой нитью, перекинутой через невесомый блок. Ось блока укреплена на неподвижной наклонной плоскости, составляющей с горизонтом угол a = 30°. При каком минимальном значении коэффициента трения тела m1 и m2 будут находиться в покое? Трением в оси блока пренебречь.
Решение
Тела будут находиться в покое, если суммы сил, действующих на каждое из них, будут равны нулю. В частности, для
тела массой m2 имеем: откуда T = m2g. Условие равновесия тела массой m1 зависит от направления силы трения покоя Fтр. Чтобы найти его, применим следующий стандартный прием. Предположим, что трение в системе отсутствует. Тогда равновесие системы будет иметь место при условии:
При m1 sina > m2 тело m1 будет двигаться вдоль наклонной плоскости вниз, а при m1sina < m2 – вверх. Поскольку сила трения покоя всегда направлена против перемещения тела, возникающего в отсутствие трения, уравнения равновесия системы можно записать в виде:
Подставляя сюда вместо Fтр
максимальное значение силы трения покоя 
после несложных преобразований найдем:
В общем виде ответ может быть записан следующим образом:
.
Подставляя численные данные,
получим: 
5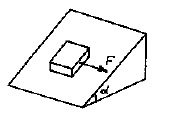 
Тело массой m = 1 кг покоится на шероховатой поверхности, составляющей с горизонтальной плоскостью угол a = 30°. С какой минимальной силой F, направленной горизонтально вдоль линии пересечения плоскостей, нужно подействовать на тело, чтобы стронуть его с места? Коэффициент трения тела о плоскость m = 0,7, ускорение свободного падения g = 10 м/с2.
Решение
Рассмотрим вначале случай,
когда сила F, приложенная к телу,
недостаточна, чтобы сдвинуть его с места. В
плоскости, на которой покоится тело, на него
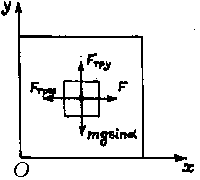
действуют силы, изображенные на рисунке, где
через Fтр х и Fтр y
обозначены проекции силы трения покоя на оси Ox
и Oy соответственно. Из условий равновесия
тела находим: 
где m – масса тела.
Согласно закону сухого трения величина силы
трения покоя 
не может превышать
значения Пусть значение силы F таково, что
скольжение еще не началось, но сила трения покоя
уже достигла своего максимального значения.
Тогда:
Очевидно, что это и есть ответ, поскольку при любом сколь угодно малом превышении величины силы F над найденным здесь значением тело придет в движение.
Продолжение следует
