Задачи из-за кордона

Закон сохранения импульса
Качественные задачи

1. Почему центр масс (ц.м.) отрезка трубы длиной 1 м находится в его средней точке, тогда как для вашей руки или ноги это не так?

Why is the cm of a 1-m length of pipe at the pipe`s midpoint, whereas this is not true for your arm or leg?

Ответ. Уточним чисто геометрическое понятие средней точки тела. Это точка, координаты которой являются средним арифметическим соответствующих минимальной и максимальной координат точек тел по всем трем координатным осям:
Распределение массы однородной трубы центрально симметрично относительно средней точки: каждой точке трубы отвечает точка трубы, расположенная центрально симметрично относительно средней точки, а плотность массы во всех точках трубы одинакова. Отсюда следует, что ц.м. трубы совпадает со средней точкой. Формально, если за начало отсчета координат принять среднюю точку, то каждой точке трубы с заданными координатами x, y, z отвечает точка трубы с противоположными координатами –x, –y, –z, а т.к. плотность r массы не зависит от координат, то вклады этих точек в координаты ц.м., dm·x = r·dV·x и dm·(–x) = r·dV·(–x), ... , взаимно компенсируются и ц.м. имеет нулевые координаты, т.е. совпадает со средней точкой.

Эквивалентное рассуждение, чисто геометрическое и бескоординатное, выглядит так. Средняя точка является центром симметрии трубы: при преобразовании инверсии относительно средней точки однородная труба переходит в себя. Стало быть, при инверсии относительно средней точки ц.м. трубы не смещается, является неподвижной точкой. С другой стороны, единственной неподвижной точкой при инверсии является центр инверсии. Значит, центр инверсии, т.е. средняя точка и ц.м. совпадают. Заодно мы показали, что у всякого тела, распределение масс которого обладает центральной симметрией относительно некоторой точки (центра симметрии), ц.м. находится в центре симметрии (совпадает с ним). Приведенные здесь аналогичные рассуждения, основанные на той или иной симметрии задачи, т.е. на инвариантности системы относительно тех или иных преобразований, носят общее название соображений симметрии.

Для нашей руки или ноги распределение массы несимметрично относительно средней точки: плотность массы не постоянна (плотность костной и мышечной ткани различна), и средняя точка отнюдь не является центром симметрии. Например, распределение массы по длине ноги сдвинуто в сторону более толстого бедра.

2. Покажите [схематически] на диаграмме, как смещается ваш центр масс, когда вы садитесь из положения лежа.

Show on a diagram how your cm shifts when you move from a lying position to a sitting position.

3. Опишите аналитический способ определения центра масс произвольной тонкой однородной треугольной пластинки.

Describe an analytic way of determining the cm of any thin, triangular-shaped, uniform plate.

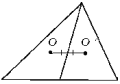Ответ. Задача, очевидно, является плоской. Рассмотрим плоскость треугольника. По соображениям симметрии ц.м. плоского однородного треугольника находится в точке пересечения его медиан. Действительно, рассмотрим следующее преобразование треугольника относительно некоторой его медианы (см. рисунок): каждую точку O треугольника переведем в точку Oў треугольника, расположенную по другую сторону от данной медианы на прямой, проходящей через точку O параллельно соответствующей стороне

треугольника (на которую опущена данная медиана) и находящуюся на том же расстоянии от медианы, что и исходная точка O. Это преобразование можно назвать преобразованием косого отражения треугольника относительно данной медианы (отражение в косоугольных координатах, задаваемых осями медиана–сторона). Оно, очевидно, переводит однородный треугольник в себя. Следовательно, при таком косом отражении ц.м. остается на месте. Но при косом отражении на месте остается только данная медиана, значит, ц.м. однородного треугольника лежит на данной медиане. Это утверждение верно для любой медианы, следовательно, ц.м. лежит на пересечении медиан. (Заодно мы получили доказательство геометрической теоремы о том, что все три медианы треугольника пересекаются в одной точке.)

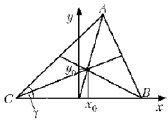Остается найти аналитически положение точки пересечения медиан, выбрав удобную систему координат. Выберем прямоугольную систему координат, когда одна из сторон треугольника CB лежит на оси x, а начало координат D лежит посередине этой стороны, совпадая с концом соответствующей медианы. Ось y направлена в сторону вершины A треугольника (см. рисунок). Треугольник ABC

полностью определяется своими сторонами CA и CB, их длины обозначены соответственно a и b, и углом g между ними (при вершине C).

AD и BE – медианы, O – точка пересечения медиан, т.е. ц.м., AF – высота, опущенная из вершины A на сторону CB (ось x).

Из геометрии известно, что длина отрезка OD составляет 1/3 длины медианы AD (точка пересечения медиан отсекает медианы со стороны ее конца). Отсюда немедленно следует (например, рассмотрением подобных прямоугольных треугольников DAF и DОx0), что координаты x0, y0 точки O, т.е. ц.м., составляют координаты вершины A, которые определяются отрезками AF и DF:

4. Встаньте лицом к торцу открытой двери. Поставьте ступни ног по обе стороны двери так, чтобы ваши нос и живот касались торца двери. Попытайтесь подняться на носки. Почему это вам это не удается?

Place yourself facing the edge of an open door. Position you feet astride the door with your nose and abdomen touching the door`s edge. Try to rise on your tiptoes. Why can`t this be done?

Ответ. В исходном положении ц.м. стоящего человека находится в его теле, над серединой ступней ног. При подъеме на носки ц.м., оставаясь в теле человека, перемещается вперед в сторону носков. В данном случае он должен был бы оказаться внутри «тела» двери, что невозможно (разумеется, если у вас обычная крепкая, а не бумажная дверь).

5. Почему невозможно, из положения сидя прямо на стуле, встать на ноги, не наклонившись предварительно вперед?

Why is it not possible to sit upright in a chair and rise to one`s feet without first leaning forward?

Ответ. В исходном положении ц.м. сидящего находится над стулом. Наклоняясь вперед, человек переносит ц.м. вперед, чтобы он оказался над находящимися перед стулом ступнями ног. После этого вертикальным усилием ног можно встать, поднимая ц.м. вверх. Если пытаться, отталкиваясь ногами вверх, подниматься без наклона вперед, возникает опрокидывающий назад момент сил.

6. Почему однородный прямоугольный кирпич можно положить на край стола, только если с края стола свисает не более половины длины кирпича?

Explain why a uniform rectangular brick can be placed so that slightly less than half its length can be suspended over the edge of a table, but no more.

Ответ. По соображениям симметрии ц.м. однородного прямоугольного кирпича находится в его средней точке, которая является центром симметрии кирпича (см. ответ на задачу 1). Кирпич не упадет со стола до тех пор, пока его ц.м., т.е. середина кирпича, находится над столом: в этом положении уравновешиваются сила тяжести и реакция стола, а также моменты этих сил. Если ц.м. кирпича, т.е. его середина, будет над полом, то равновесие моментов этих сил относительно края стола уже невозможно: кирпич поворачивается вокруг края стола и соскальзывает на пол.

7. Почему вы вынуждены отклоняться назад, когда несете в руках тяжелый груз?

Why do you tend to lean backward when carrying a heavy load in your arms?

Ответ. Говоря кратко, чтобы при нормальной ходьбе или стоя уравновесить опрокидывающий вперед момент силы тяжести груза на руках. Общий центр тяжести системы человек плюс груз на руках должен находиться над опорой, между идущими ногами. Отклоняясь назад, мы добиваемся этого, перенося назад собственный центр тяжести.

В противном случае придется быстро бежать вперед (что можно иногда наблюдать), компенсируя опрокидывающий момент частыми усилиями попеременно выставляемых вперед ног.

8. Если только внешняя сила может изменить импульс центра масс тела, то каким образом внутренняя сила двигателя может ускорить автомобиль?

If only an external forxe can change the momentum of the center of mass of an object, how can the internal force of the engine accelerate a car?

Ответ. Внутренние силы двигателя вращают колеса автомобиля, причем скорость и направление их вращения можно менять, регулируя режим работы двигателя. Движение автомобиля как целого, т.е. движение его центра масс, возможно только при контакте колес с внешней поверхностью (например дорожным покрытием), т.е. при взаимодействии с внешним телом. Вообще говоря, этот контакт и это взаимодействие колес с внешним телом – весьма сложное явление. В частности, оно определяется свойствами поверхности. Если поверхность твердая и колеса не проскальзывают (например, трение о дорожное покрытие достаточно велико), то они отталкиваются от внешней поверхности, причем сила отталкивания и ее направление определяются скоростью и направлением вращения колес. Соответственно, по третьему закону Ньютона, внешняя сила реакции поверхности (дорожного покрытия) ускоряет автомобиль. Если, наоборот, сцепление колес с внешней поверхностью недостаточно (например, в случае скользкой ледяной дороги), то автомобиль буксует. Каждый может вспомнить многочисленные промежуточные стадии: мокрый асфальт, жидкая грязь грунтовой дороги, болото и т.д.

9. Как может ракета изменить направление, когда она находится далеко в космическом пространстве и, по существу, в вакууме?

How can a rocket change direction when it is far out in space and essentially in a vacuum?

Ответ. Не изменяя общего импульса всей системы (ракетоноситель плюс топливо), можно перераспределять импульсы отдельных ее частей. Желая изменить направление полета ракетоносителя, нужно создать за счет работы двигателя реактивную струю газов, грубо говоря, в противоположном направлении.