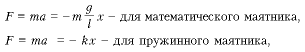
В школьном курсе физики изучаются два вида механических колебательных систем: математический и пружинный маятники. Сравнение и анализ уравнений колебаний в этих системах позволяют сделать вывод: колебания в обоих случаях являются гармоническими, т.е. происходят по законам синуса или косинуса (впоследствии этот вывод обобщается и на электромагнитные колебания в колебательном контуре):
где m – масса колеблющегося тела, a – его ускорение, g – ускорение свободного падения, l – длина маятника, x – смещение тела от положения равновесия, k – коэффициент жесткости пружины. Оба уравнения можно записать в общем виде:
где w0 – собственная циклическая частота колебаний. Как видим, ускорение при гармонических колебаниях прямо пропорционально величине смещения тела от положения равновесия. Знак «–» указывает на то, что направление смещения тела от положения равновесия и направление действия возвращающей силы противоположны.
Хотя далеко не все
механические колебательные системы
представляют собой в явном виде пружинный
или математический маятники, многие из них можно
представить как их комбинацию. Другими словами, любые
механические колебания, в которых возвращающая
сила прямо пропорциональна величине смещения
колеблющегося тела от положения равновесия,
происходят по гармоническому закону. Такие
возвращающие силы называют квазиупругими. В
общем случае период колебаний можно
рассчитывать по формуле 
или 
если
определиться, что в каждом конкретном случае
будет играть роль массы колеблющегося тела, что
– роль жесткости пружины («гравитационной»,
«пневматической», «гидравлической»,
«фрикционной» и т.п.), что - длины маятника.
Задачи на выявление аналогий с пружинным или математическим маятником встречаются в сборниках задач, но к сожалению, только по одной-две, что не позволяет учащимся выработать системный подход к их решению. Вот и приходится учителю листать задачники, в основном старые, изданные лет 20–30 назад. Приведем несколько задач и их решения в общем виде.
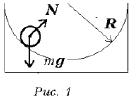Задача 1. По внутренней
поверхности полусферической чаши радиусом
кривизны R свободно скользит маленький шарик.
Найдите период его малых колебаний.
Итак, выполним рисунок и покажем на нем силы, под действием которых происходит движение (рис. 1). Малость размеров шарика позволяет считать его материальной точкой. Видно, что «расстановка» сил и их действие такие же, как в случае математического маятника, с тем лишь отличием, что
вместо силы натяжения нити действует сила реакции опоры. Применяем закон колебаний математического маятника, заменяя в формуле для периода колебаний длину маятника на радиус чаши:
Задача 2. Вблизи поверхности
Земли прорыт сквозной прямой туннель. В нем
проложили рельсы и пустили вагонетку, которая
движется без сопротивления. Каким будет период
свободных колебаний вагонетки (от одного выхода
туннеля до другого и обратно)? Радиус Земли равен R.
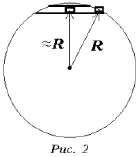
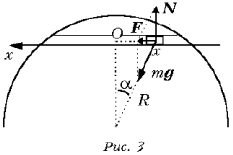
Слова «вблизи поверхности» позволяют считать, что расстояние от центра Земли до вагонетки практически постоянно и равно R и что амплитуда колебаний мала по сравнению с ним (рис. 2). Проведем координатную ось x и отметим на ней положение равновесия вагонетки – точку O (рис. 3). Покажем силы, действующие на вагонетку в какой-либо произвольной точке x.
Оказывается, и эта ситуация
сводится к математическому маятнику, а сила
тяготения играет роль силы натяжения нити. Но для
описания характера движения не важна природа
действующих сил, главное, что их
равнодействующая F направлена вдоль
туннеля к положению равновесия и
пропорциональна смещению. Итак, мысленно
перевернув систему, считаем ее подобной
математическому маятнику и применяем формулу 
.
Проверим наш подход математически.
Запишем векторное уравнение для
равнодействующей силы:
N + mg = F = ma.
Вдоль координатной оси Оx:
mg sin a = ma Ю g sin a = a.
С другой стороны, угол a можно
связать и с расстояниями. Учитывая что мы
«перевернули» вагонетку, получим: 
Подставив это выражение в
предыдущее, получим: 
Отметим,
что ускорение прямо пропорционально смещению
вагонетки от положения равновесия (координате x).
Это очень важно, поскольку именно этот факт
позволяет нам считать колебания вагонетки
гармоническими с периодом 
Задача 3. В U-образную стеклянную трубку постоянной площадью поперечного сечения S налита ртуть массой m. Плотность ртути r. Найдите период колебаний ртути после того, как трубку качнули.
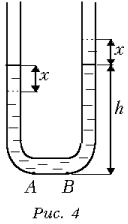Сначала, как обычно, выполним
схематический рисунок, на котором покажем
начальные уровни столбов ртути в обоих коленах
трубки, а также (пунктиром) положения этих
уровней при наклоне (рис. 4). Величину
отклонения обозначим x. Как известно, при
открытых обоих коленах уровни в них в равновесии
равны, т.к. равны их гидростатические давления
(давления pА и pВ на дно соответственно в
точках А и В). Если
уровни жидкости в коленах оказались разными, то возникает разность давлений и сила, стремящаяся возвратить жидкость в равновесное состояние.
Пусть в некоторый момент в левом колене высота столба ртути уменьшилась на величину x, а в правом – на столько же возросла. Возникла разность гидростатических давлений:
Отсюда находим численное значение возвращающей силы F, учитывая, что направление смещения столбика ртути в колене противоположно направлению действия этой возвращающей силы:
С другой стороны, согласно второму закону Ньютона F = ma, где m – масса тела, на которое действует сила. Возвращающая сила благодаря силам межмолекулярного взаимодействия действует на все количество ртути, находящейся в трубке, т.е. в данном случае m – масса всей ртути. Отсюда:
Важно, что в полученном
выражении возвращающая сила прямо
пропорциональна смещению x, т.е. колебания
будут гармоническими. Величина 2rgS играет
роль коэффициента жесткости «гидравлической»
пружины. Поэтому окончательное выражение для
периода: 
Перейдем к другому примеру «гидравлической» пружины, действие которой обусловлено не разницей гидростатических давлений, а действием выталкивающей (архимедовой) силы и силы тяжести.
Задача 4. На поверхности воды плотностью r плавает бутылка массой m и площадью поперечного сечения S. Найдите период свободных вертикальных колебаний бутылки при условии, что в воде находится только ее цилиндрическая часть (т.е. горлышко в воду не погружается).
Начинаем, разумеется, с рисунков. На левом покажем бутылку в равновесном положении, глубину ее погружения h и действующие на бутылку силы (рис. 5, a), на правом – бутылку в «притопленном» на глубину x положении (рис. 5, б).
В начальном (равновесном) положении:
В «притопленном» положении на бутылку действует такая же сила тяжести и возросшая архимедова сила FА', т.к. увеличился объем погруженной части бутылки. Равнодействующая этих сил не равна нулю и направлена вверх. Следовательно:
Подставив в это выражение формулу (3), получаем:
Выразим величины сил FА и FА' через объем погруженной части бутылки. Так как она имеет форму цилиндра c основанием S, то в равновесном состоянии объем погруженной части V = Sh, а в «притопленном» V ' = S(h + x). Соответственно силы равны:
После подстановки этих выражений в формулу (4), получим:
При расчете объема мы учитывали только модуль x. Поскольку направление дополнительного погружения бутылки противоположно направлению действия равнодействующей силы, запишем:
Снова ускорение прямо пропорционально величине смещения тела от положения равновесия, т.е. колебания гармонические. Величина rgS выполняет функцию коэффициента жесткости «гидравлической» пружины (k = rgS). Отсюда:
Задача 5. Цилиндрический сосуд длиной 2l расположен горизонтально. Посередине цилиндра находится в равновесии тонкий легкоподвижный поршень массой m и площадью S. Справа и слева от поршня давление воздуха составляет p0. Найдите период малых колебаний поршня.
Возникает вопрос: а как этих колебаний добиться, ведь поршень находится внутри закрытого сосуда? Ответ: например, встряхнув цилиндр. Далее, обратим внимание на то, что речь идет о колебаниях малой амплитуды, что позволяет считать колебательный процесс в обоих отсеках сосуда изотермическим и применить закон Бойля–Мариотта. [При реальных значениях параметров колебания, так же как и при распространении звука в воздухе, будут адиабатическими. Изотермичность колебаний необходимо дополнительно ввести в условие задачи. – Ред.] Затем, поскольку поршень тонкий, можно считать начальную длину каждого отсека равной l – половине длины всего цилиндра. Наконец, поршень, по условию, движется легко, т.е. трения между поршнем и стенками сосуда нет.
Решение начинаем, как обычно, с рисунков. На рис. 6, а покажем цилиндр при равновесном положении поршня, обозначим длины отсеков и давление газа в них, на рис. 6, б – цилиндр со смещенным на расстояние x поршнем и давления газа в отсеках.
Применим закон Бойля–Мариотта к газу в левом отсеке:
где V0 = lS – объем левого отсека при равновесном положении поршня, V1 = (l – x)S – при смещенном. Выполнив те же действия для правого отсека, получаем:
Наличие возвращающей силы обусловлено разностью давлений газа слева и справа от поршня. Эту силу согласно второму закону Ньютона можно связать с ускорением, сообщаемым поршню:
Выражая p1 из уравнения (2) и подставляя его в выражение (3), получаем:
Аналогично, выражая p2
из уравнения (1) и подставляя его в (3): 
Вспомним, что колебания малые: если x мало, то x2 – малая величина, которой можно пренебречь на фоне l2:
Сделаем еще один шаг: поскольку направления возвращающей силы F и смещения противоположны, то в одну из частей последнего равенства добавим «–»:
т.е. и в этой колебательной
системе ускорение прямо пропорционально
координате. Сравнение этого уравнения с
уравнением колебаний груза на пружине 
позволяет сделать вывод, что
величина
играет роль коэффициента жесткости
«пневматической» пружины для поршня массой m.
Период малых колебаний поршня равен 
Наконец рассмотрим самую сложную задачу - про «фрикционную пружину».
Задача 6. Два одинаковых ролика вращаются с одинаковой угловой скоростью в противоположные стороны. Ролик слева – по часовой стрелке, ролик справа – против часовой стрелки. Оси вращения роликов лежат в горизонтальной плоскости, расстояние между ними l. На ролики положена доска, коэффициент трения которой о ролики равен m. Изначально центр доски находился на одинаковом расстоянии от осей роликов. Если ролики начнут вращаться одновременно, то доска останется в равновесии (в состоянии покоя). Но если доску чуть-чуть подтолкнуть вдоль ее длины, то она начнет совершать колебания на роликах в горизонтальной плоскости. Найдите период этих колебаний.
Итак, изобразим эту систему и обозначим силы при равновесном положении доски (рис. 7). Сила тяжести mg компенсируется силами реакции опор N1 и N2. Если доску сдвинуть на расстояние x, то нагрузка на ролики перераспределится. Ролик с большей нагрузкой будет действовать на доску с большей силой трения, ролик с меньшей нагрузкой – с меньшей; в результате доска начнет двигаться в направлении, обратном смещению. Она по инерции пройдет положение равновесия, нагрузка на ролики вновь перераспределится, и теперь уже другой ролик заставит доску двигаться в обратную сторону и т.д. Возникнут колебания.
Рассмотрим смещенное положение доски. Пусть x – величина смещения в какую-либо сторону (рис. 8). Для определения сил реакции опор покажем плечи этих сил и плечи силы тяжести относительно точек O1 и O2
(см. верхнюю часть рисунка). Как известно, если тело не вращается, то алгебраическая сумма моментов всех сил, действующих на него, равна нулю (отсчитывать моменты можно относительно любой точки, если векторная сумма сил, создающих эти моменты, равна нулю. Это существенно):
Найдем отсюда силы реакции опор:
Поскольку при смещении равновесие доски нарушилось, то:
Fтр1 + Fтр2 = ma.
Величина силы трения (скольжения) зависит от силы реакции опоры: Fтр = mN. Так как N1 > N2, то Fтр1 > Fтр2. Следовательно, вектор ускорения a направлен в ту же сторону, что и вектор Fтр1. Поэтому при проецировании последнего векторного равенства на ось x, получается:
Выражая силы трения через соответствующие силы реакции опор, находим:
Подставляя эти выражения в (4)
для расчета ускорения и упрощая, имеем: 
С учетом направления смещения
x (оно противоположно направлению
возвращающей силы) получаем уравнение: 
которое указывает на гармонический характер колебаний доски на роликах.
Сравнивая его с уравнением
колебаний груза на пружине 
мы
видим, что 
играет роль 
откуда период колебаний 
Разумеется, множество задач на «скрытые пружины» не исчерпывается приведенными выше, но наша цель состояла в выработке системного подхода к их решению. Будем надеяться, что кто-нибудь из читателей продолжит этот список.
