О.Ю.Шведов,
А.А.Якута,
М.В.Семенов, С.Д.Варламов,
Р.Ю.Компанеец, А.В.Андрианов,
В.А.Погожев, А.В.Селиверстов
Задача 4
Нагрузка подключена к источнику выходным напряжением U = 2 кВ с помощью длинной двухполосковой линии. Полоски имеют ширину a = 4 см и расположены на расстоянии b = 4 мм параллельно одна над другой. При некотором сопротивлении нагрузки, много большей сопротивления проводников линии, сила их взаимодействия равна нулю. Какой по величине и куда направленной будет указанная сила в расчете на единицу длины линии, если сопротивление нагрузки увеличить в n = 5 раз?
Решение
На полоски линии действуют две силы: кулоновская сила электростатического притяжения, обусловленная наличием на поверхности полосок зарядов, и сила Ампера, связанная с протеканием тока и отталкивающая полоски друг от друга. Согласно условию при некотором сопротивлении нагрузки R0 сила взаимодействия проводников равна нулю. Это означает, что при данном сопротивлении силы Кулона и Ампера уравновешивают друг друга. Вычислим кулоновскую силу, приходящуюся на единицу длины линии. Выделим участок длиной l. Пусть на нем имеется заряд q. Тогда:
В этой формуле E – напряженность электрического поля между полосками линии, которая представляет собой плоский конденсатор. Здесь учтено, что кулоновская сила равна произведению заряда, находящегося на рассматриваемом участке полоски, на величину напряженности поля, создаваемого другой полоской, которая равна E/2. Выразим погонную (в расчете на единицу длины) кулоновскую силу через величины, известные из условия задачи:
Здесь 
– емкость плоского
конденсатора, приходящаяся на единицу длины
линии.
Теперь найдем силу Ампера, приходящуюся на единицу длины линии. Она пропорциональна силе тока, протекающего через каждую из полосок, а потому пропорциональна квадрату силы тока:
Коэффициент пропорциональности B можно найти, приравнивая FK/l и FA/l:
Из полученных формул следует, что после увеличения сопротивления нагрузки в n = 5 раз кулоновская сила не изменится, а сила Ампера уменьшится в n2 раз. Значит, после увеличения сопротивления полоски линии будут притягиваться. Сила их притяжения f, приходящаяся на единицу длины, будет равна разности сил Кулона и Ампера:
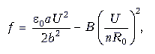
откуда, с учетом выражения для B, получается:
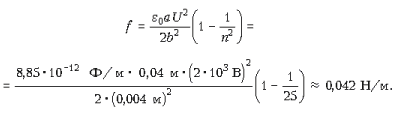
Задача 5
На каком расстоянии от въезда на
станцию метро находится поезд, когда пассажир,
стоящий на краю платформы около конца тоннеля,
начинает видеть блик от света фар на рельсах?
Перед въездом на станцию расположен достаточно
длинный поворот радиусом закругления R.
Считать, что тоннель горизонтален, а его сечение
– прямоугольник шириной l << R,
расстояние между рельсами h << R,
фары поезда расположены точно над рельсами,
профиль рельса изображен на рисунке.
Решение
Прежде всего заметим, что луч, который видит пассажир, отражается от головки рельса, которая имеет округлую форму. Поэтому при большом радиусе закругления рельсов (и следовательно, при углах падения и отражения луча, близких к p/2) можно пренебречь тем, что глаза пассажира и фары метропоезда находятся на разной высоте над уровнем рельсов, и считать, что фары, глаза пассажира и точка рельса, от которой отражается свет, лежат в практически горизонтальной плоскости. Далее необходимо рассмотреть два случая: когда тоннель закругляется в сторону платформы, на которой стоит пассажир, и когда тоннель закругляется в противоположную от пассажира сторону.
Рассмотрим сначала первый случай. Из рисунка видно, что прежде всего пассажир увидит луч от правой фары, отраженный правым рельсом.
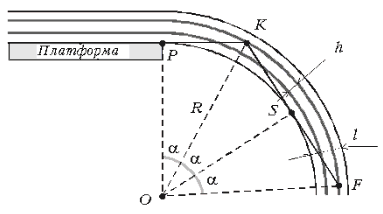
Отрезки, проведенные из центра кривизны пути (точка O) к фаре (точка F), пассажиру (точка P), точке отражения света от рельса (K) и точке, в которой луч касается стенки тоннеля (S), составляют друг с другом равные углы a. Из треугольника OPK при малых a можно приближенно найти расстояние от внутренней стенки тоннеля до внешнего рельса:
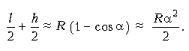
Отсюда
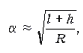
а искомое расстояние:
Рассмотрим второй случай. Он отличается от первого тем, что луч касается стенок тоннеля дважды – в точках S и S1. Отрезки OF, OS1, OK и OS по-прежнему образуют между собой одинаковые углы a, совпадающие с углом, найденным в предыдущем случае. Отрезок же OP составляет с отрезком OS некоторый угол b, который можно оценить из треугольника OPS при малых b с помощью следующего соотношения:
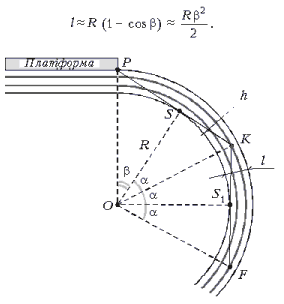
Отсюда 
, и искомое расстояние: 
Второй теоретический тур
8-й класс
Задача 1
Автомобиль движется с постоянной скоростью. В начале движения секундная стрелка часов с обломанной минутной стрелкой показывает 0 секунд, через 3 км – 30 секунд, еще через 4 км – 50 секунд. Найдите скорость автомобиля, если известно, что она больше 40 км/ч.
Решение
По часам с обломанной минутной стрелкой можно установить, что первые 3000 м автомобиль проходит за (60m + 30) с, где m – целое неотрицательное число. Поэтому величина 1/v, где v – скорость автомобиля, может принимать следующий ряд значений:
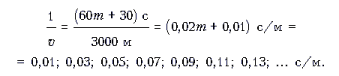
Следующие 4000 м автомобиль проходит за (60n + 20) с, где n – целое неотрицательное число. Поэтому, с другой стороны, величина 1/v может принимать следующий ряд значений:
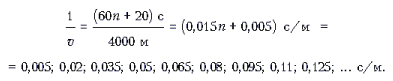
Так как автомобиль движется с постоянной скоростью, то величина 1/v может принимать только те значения, которые встречаются и в первой, и во второй последовательностях чисел:
По условию задачи скорость
автомобиля v > 40 км/ч » 11,1 м/с. Значит, 
Таким образом, из набора
возможных значений, которые может принимать
величина 1/v, условию задачи удовлетворяет
единственное: 1/v=0,05. Отсюда скорость
автомобиля v = 20 м/с = 72 км/ч.
Задача 2
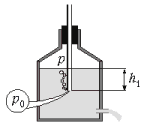В боковой стенке бутылки проделано
маленькое отверстие, в которое вставлена
затычка. В бутылку наливают воду и закрывают ее
горлышко пробкой, через которую пропущена
трубка. Длина трубки подобрана таким образом, что
ее нижний конец находится выше отверстия в
стенке бутылки, но ниже поверхности воды, а
верхний конец сообщается с атмосферой. Затычку
из отверстия в боковой стенке вынимают, и из него
начинает вытекать вода. Через некоторое время
поток воды из отверстия устанавливается, и вода
вытекает с постоянной скоростью. Найдите
давление воздуха p, находящегося в бутылке, в
тот момент, когда нижний конец трубки находится
на глубине h = 5 см от поверхности воды.
Плотность воды r = 1000 кг/м3, атмосферное
давление p0 = 100 000 Па.
Решение
В любой момент времени
давление в жидкости на уровне нижнего конца
трубки равно p + rgh1, где p – давление
воздуха в бутылке,
h1 – глубина, на которую погружен в воду
нижний конец трубки. До вынимания затычки
давление воздуха в бутылке было равно
атмосферному давлению p0. Значит,
давление на уровне нижнего конца трубки было
равно p0 + rgh1. Ясно, что давление на
уровне отверстия в боковой стенке было еще
больше (отверстие находится глубже нижнего конца
трубки), поэтому после вынимания затычки вода
начинает вытекать из бутылки, объем воздуха над
поверхностью воды увеличивается, и давление
воздуха в бутылке постепенно падает. Так будет
продолжаться до тех пор, пока давление на уровне
нижнего конца трубки не станет равно
атмосферному. Как только это случится, через
трубку в бутылку станут входить пузырьки воздуха
и вода станет вытекать из отверстия с постоянной
скоростью (см. рисунок). Значит, начиная с этого
момента, справедливо соотношение p0 = p
+ rgh1,
откуда для момента, когда нижний конец трубки
находится на глубине h = 5 см, p0 = p
+ rgh,
и
p = p0 – rgh = 100 000 – 1000Ч9,8Ч0,05 = 99 510 (Па).
Задача 3
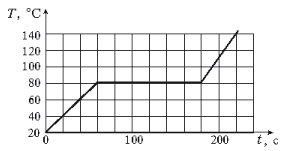
В металлический стакан налили m = 40 г жидкости и начали нагревать стакан на спиртовке, непрерывно измеряя его температуру. В результате был получен график зависимости температуры стакана от времени, приведенный на рисунке. Пользуясь графиком, найдите удельную теплоемкость Cж и удельную теплоту парообразования Lж жидкости, налитой в стакан, если в спиртовке ежесекундно сгорает m = 11 мг спирта. Удельная теплота сгорания спирта q = 27 кДж/г. Потерями тепла пренебречь.
Решение
Так как спирт сгорает с постоянной скоростью, то количество теплоты, переданное системе, прямо пропорционально времени нагрева. Из графика следует, что в течение первых 60 с температура системы линейно возрастала от 20 до 80 °C (стакан и жидкость нагревались), затем в течение 120 с температура оставалась неизменной (жидкость кипела и испарялась), и наконец, за последние 40 секунд температура системы линейно увеличивалась от 80 до 140 °C (вся жидкость выкипела, нагревался пустой стакан). Найдем количества теплоты, которые поступили в систему за каждый промежуток времени.
В течение времени Dt1 = 60 с в систему поступило количество теплоты DQ1 = mqDt1, в течение Dt2 = 120 с поступило DQ2 = mqDt2, в течение Dt3 = 40 с поступило DQ3 = mqDt3. Составим уравнения теплового баланса для каждого промежутка времени:
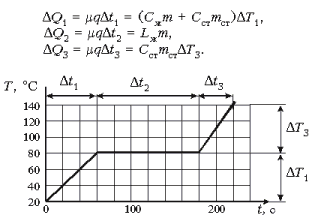
Здесь Cст и mст – удельная теплоемкость и масса стакана соответственно, DT1 = DT3 = 60 °C. Из второго уравнения можно сразу найти удельную теплоту парообразования жидкости:
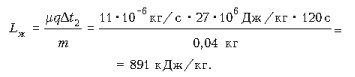
Из третьего уравнения можно выразить произведение Cстmст:
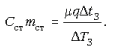
Подставляя полученное произведение в первое уравнение и учитывая, что DT1 = DT3, найдем удельную теплоемкость жидкости:
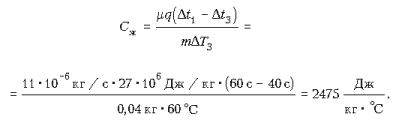
9-й класс
Задача 1
Какой минимальный путь за время t может пройти тело, движущееся с постоянным ускорением а?
Решение
Легко сообразить, что путь минимален, если тело движется по прямой. Действительно, введем прямоугольную систему координат и направим ось x вдоль вектора ускорения а. Тогда проекции скорости тела на координатные оси зависят от времени t по следующим законам:
vx(t) = vx0 + at; vy(t) = vy0; vz(t) = vz0.
Здесь vx0, vy0, vz0 – проекции скорости тела на соответствующие оси при t = 0. Если положить vy0 = vz0 = 0, то скорость тела в каждый момент времени t будет меньше, чем она была бы при отличных от нуля vy0 и vz0. Поэтому будет меньше и пройденный путь. Значит, для решения задачи нужно рассматривать движение тела вдоль прямой, параллельной оси x.
При таком движении возможны три случая, различающиеся по знакам скорости в течение времени движения t:
а) vx(t) > 0 при 0 Ј t Ј t;
б) vx(t) < 0 при 0 Ј t Ј t;
в) vx(t) < 0 при 0 Ј t < t0 и vx(t) > 0 при t0 < t Ј t.
Отметим, что во всех случаях a > 0. В случае а пройденный путь совпадает с перемещением и равен
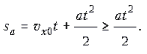
В случае б пройденный путь – это перемещение, взятое с обратным знаком:
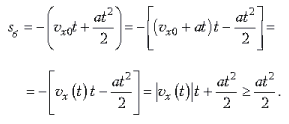
Наконец, в случае в пройденный путь складывается из двух отрезков, пройденных телом до и после «точки поворота» (точки, в которой скорость тела обращается в нуль при t = t0). Первый отрезок пути может быть найден из формулы, полученной при рассмотрении случая б, путем подстановки t = t0:
(здесь учтено, что vx(t0) = 0). Второй же отрезок равен:
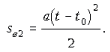
Таким образом, весь пройденный путь равен:
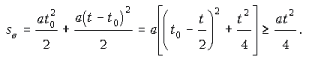
Значит, минимальным
является путь, который тело проходит в случае в:
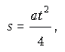
причем «точка поворота» должна приходиться на середину промежутка времени движения t.
Задача 2
На рисунке вы видите изображение
идущих часов, полученное с помощью компьютерного
сканера. Принцип его работы прост. Мощная лампа
создает на сканируемом объекте узкую освещенную
полоску, а отраженный свет попадает на набор
фотодатчиков, которые расположены в виде
линейки, параллельной этой полоске. И лампа, и
линейка датчиков расположены на подвижной
каретке. Каретка движется с постоянной
скоростью, и датчики через равные интервалы
времени передают в компьютер изображение. Таким
образом, при перемещении каретки получается
много «срезов» объекта, из которых и состоит
изображение. Пользуясь данным изображением,
определите направление и скорость движения
каретки сканера, если длина секундной стрелки (от
оси до острия) составляет 15 мм.
Решение
Направление сканирования определяется просто. Очевидно, кривизна изображения стрелки максимальна там, где скорость каретки была направлена вдоль стрелки. На рисунке максимальная кривизна соответствует точкам вблизи оси, причем стрелка в этот момент была направлена почти «вертикально», т.е. от цифры «12» к цифре «6». Значит, сканирование осуществлялось в вертикальном направлении. Проведем касательную к секундной стрелке в точке ее крепления к оси. Деление на циферблате, на которое «покажет» касательная, есть момент начала или конца сканирования стрелки (в зависимости от того, вверх или вниз движется каретка). Проводя касательную, убедимся, что она «упирается» в деление, соответствующее 28 с, в то время как острие стрелки показывает 20 с, т.е. меньшее время. Значит, каретка сканера пересекла острие секундной стрелки раньше, чем ее ось, и каретка двигалась от цифры «6» к цифре «12». Отсюда сразу же можно найти время Dt, за которое каретка просканировала стрелку: 28 – 20 = 8 с.
Теперь найдем скорость каретки. Расстояние, которое прошла каретка за время Dt, равно расстоянию от острия секундной стрелки до прямой, проходящей через ось и цифру «3» на циферблате. Обозначим его через L. На рисунке это расстояние равно L1 = 11 мм. Кроме того, длина секундной стрелки на рисунке равна l1 = 20 мм, а по условию задачи истинная длина стрелки l = 15 мм. Так как при увеличении рисунка все размеры изменились в одинаковое число раз (изображение не искажено), то справедлива пропорция:
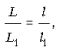
поэтому скорость каретки:
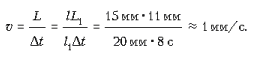
Задача 3
Сферическая дробинка диаметром d1 и плотностью rд падает в жидкости плотностью rж = rд/8 со скоростью v1. Дробинка диаметром d2 = 2d1 падает в той же жидкости со скоростью v2 = 4v1. С какой скоростью будет всплывать в этой жидкости сферический пузырек воздуха диаметром d3 = 1,5d1? Считать силу вязкого трения, действующую на шарик в жидкости, пропорциональной скорости шарика.
Решение
При движении шарика в жидкости на него действуют сила тяжести, сила Архимеда и сила вязкого трения, зависящая, как это следует из условия задачи, от скорости и от диаметра шарика. Две первые силы являются объемными. Это значит, что их сумма пропорциональна разности кr – rжп (r – плотность шарика) и объему шарика, т.е. кубу его диаметра d. Третья сила пропорциональна произведению vdn, где v – скорость шарика, n – неизвестный показатель степени. При движении с постоянной скоростью сумма сил тяжести и Архимеда равна по модулю силе вязкого трения. Тогда для дробинки диаметром d1 имеем:
откуда, с учетом условия задачи, получаем:
Аналогично, для дробинки диаметром d2:
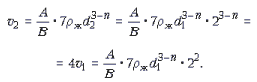
Отсюда получаем уравнение решая которое, находим показатель степени: n = 1.
Теперь можно найти скорость, с которой всплывает пузырек воздуха. Пренебрегая массой воздуха, получаем:
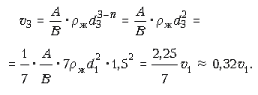
Задача 4
В «черном ящике» с тремя контактами находится схема, составленная из батарейки с известной ЭДС, двух неизвестных резисторов и соединительных проводов. Амперметр, подключенный к контактам 1 и 2, показывает значение тока I, к контактам 1 и 3 – ток 2I, а к контактам 2 и 3 – отсутствие тока. Чему могут быть равны сопротивления резисторов? Сопротивлением батарейки, амперметра и соединительных проводов пренебречь.
Решение
Из условия задачи вытекает, что:
– никакие две клеммы не могут быть подключены только к батарейке (иначе бы амперметр при подключении к этим клеммам зашкаливало);
– никакие две клеммы не могут быть соединены друг с другом только соединительным проводом (иначе бы два тока из трех совпадали);
– между клеммами 2 и 3 включен только резистор.
Поэтому возможны только следующие схемы:
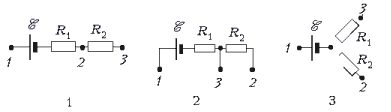
Запишем с учетом условия задачи закон Ома для каждой схемы.
Для схемы 1:
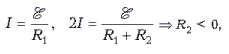
значит, такое соединение невозможно.
Для схемы 2:
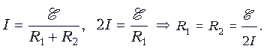
Для схемы 3:
В итоге получаем, что возможны два варианта:
1-й: резисторы равны
и подсоединены последовательно к батарейке;
2-й:оба резистора подсоединены к одному полюсу батарейки.
10-й класс
Задача 1
В неоднородной вязкой среде сила
сопротивления, действующая на тело массой m,
пропорциональна квадрату скорости, причем
коэффициент пропорциональности a зависит от
координаты тела x в направлении движения.
Какой должна быть зависимость a(x), чтобы при
любой начальной скорости, направленной вдоль оси
x, тело, пущенное из точки x = 0,
двигалось в данной среде равнозамедленно? Силу
тяжести не учитывать.
Решение
Так как тело движется вдоль оси x, то его ускорение в соответствии со вторым законом Ньютона равно:
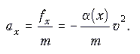
Из условия задачи следует, что тело, пущенное в начальный момент времени из начала координат с начальной скоростью v0, движется равнозамедленно. Обозначим ускорение тела ax при данных начальных условиях через –a = const. Координата тела x и его скорость v зависят от времени t следующим образом:
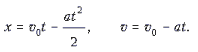
Отсюда: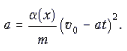 
Поэтому: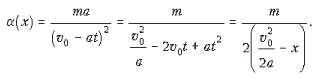 
Таким образом, тело,
пущенное из начала координат со скоростью v0,
может двигаться равнозамедленно только тогда,
когда зависимость a(x) имеет вид: 
где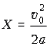 
– некоторое
положительное число.
Отметим, что X имеет смысл
расстояния, которое проходит тело от начала
координат до полной остановки, и зависит только
от свойств среды. При этом последнюю формулу
следует понимать в том смысле, что тело, пущенное
с некоторой скоростью v0, движется с
ускорением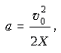 
, которое определяется начальной
скоростью и свойствами среды.
Нас не должно удивлять наличие в выражении для a(x) массы тела m. При другой массе m', но тех же размерах, форме и начальной скорости, движение тела в среде с a(x), соответствующей массе m, уже не будет равнозамедленным!
Итак,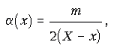 
где X –
произвольная положительная постоянная.
Задача 2
Края симметричной относительно центра невесомой сетки из упругих нитей закреплены на неподвижном горизонтальном обруче. В горизонтальном положении сетка не натянута. С какой высоты H гимнаст должен упасть без начальной скорости в центр сетки, чтобы ее максимальный прогиб оказался равным L, если под неподвижно лежащим в центре сетки гимнастом этот прогиб равен l? Размеры гимнаста, величины L и l много меньше радиуса обруча. Известно, что при e << 1 справедлива формула (1 + e)a » 1+ ae.
Решение
Пусть сетка состоит из N радиальных нитей, а жесткость каждой из них равна k. При смещении центра сетки вниз на расстояние Dx << R сила упругости F, действующая со стороны сетки на находящегося в ее центре гимнаста, направлена вертикально вверх в силу
центральной симметрии, причем:
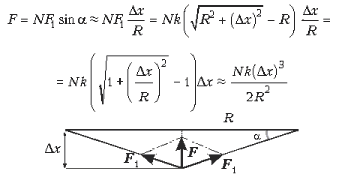
(для преобразования квадратного корня использована формула, приведенная в условии задачи). Здесь F1 – сила упругости, действующая на гимнаста со стороны каждой из нитей. Из условия известно, что когда гимнаст лежит в центре сетки неподвижно, она прогибается на l. При этом действующая на гимнаста сила тяжести mg уравновешивается силой F. Значит, условие равновесия гимнаста:
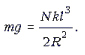
Рассмотрим далее падение гимнаста с высоты H. Перед падением его потенциальная энергия (относительно уровня ненатянутой сетки) была равна mgH. В момент же максимального прогиба сетки она складывалась из энергии в поле силы тяжести –mgL (отрицательна) и энергии упругой деформации сетки:
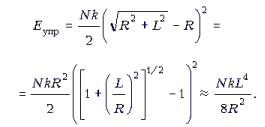
Тогда из закона сохранения механической энергии получаем:
Используя условие равновесия, находим:
